Навигация
Производная, дифференциал и интеграл
по высшей математике
Содержание:
1. Пределы последовательностей и функций. 2
2. Производная и дифференциал. 3
3 Геометрические изложения и дифференцированные исчисления (построение графиков) 4
4. Неопределенный интеграл. 7
5. Определенный интеграл. 9
6. Функции нескольких переменных, дифференцированных исчислений. 11
Литература. 12
1. Пределы последовательностей и функций
Числовой последовательностью ![]() называется числовая функция, определенная на множестве натуральных чисел. Задать числовую последовательность означает задать закон, по которому можно определить значение любого члена последовательности, зная его порядковый номер п; для этого достаточно знать выражение общего или п-го члена последовательности в виде функции его номера:
называется числовая функция, определенная на множестве натуральных чисел. Задать числовую последовательность означает задать закон, по которому можно определить значение любого члена последовательности, зная его порядковый номер п; для этого достаточно знать выражение общего или п-го члена последовательности в виде функции его номера: ![]() .
.
В основе всех положений математического анализа лежит понятие предела числовой последовательности. Число А называется пределом числовой последовательности ![]() , если для любого сколь угодно малого положительного числа e существует такой номер
, если для любого сколь угодно малого положительного числа e существует такой номер ![]() , зависящий от выбранного e, начиная с которого все члены последовательности отличаются от А по модулю меньше, чем на e, т. е.
, зависящий от выбранного e, начиная с которого все члены последовательности отличаются от А по модулю меньше, чем на e, т. е.
![]() при
при ![]() .
.
Если последовательность ![]() имеет предел А, то она называется сходящейся (к числу А) и этот факт записывают следующим образом:
имеет предел А, то она называется сходящейся (к числу А) и этот факт записывают следующим образом:
![]() .
.
Пусть функция ![]() определена в некоторой окрестности точки
определена в некоторой окрестности точки ![]() . Выберем в некоторой окрестности этой точки какую-нибудь последовательность
. Выберем в некоторой окрестности этой точки какую-нибудь последовательность ![]() сходящуюся к точке
сходящуюся к точке ![]() :
: ![]() . Значения функции в выбранных точках образуют последовательность
. Значения функции в выбранных точках образуют последовательность ![]() ,
и можно ставить вопрос о существовании предела этой последовательности.
,
и можно ставить вопрос о существовании предела этой последовательности.
Число А называется пределом функции ![]() в точке
в точке ![]() , если для любой сходящейся к
, если для любой сходящейся к ![]() последовательности значений аргумента, отличных от
последовательности значений аргумента, отличных от ![]() , соответствующая последовательность значений функции сходится к числу А, т. е.
, соответствующая последовательность значений функции сходится к числу А, т. е.
![]() .
.
Возможно иное определение предела функции в точке: число А называется пределом функции при ![]() , если для всякого положительного числа e можно указать другое положительное число d (зависящее от выбора e) такое, что абсолютная величина разности
, если для всякого положительного числа e можно указать другое положительное число d (зависящее от выбора e) такое, что абсолютная величина разности ![]() будет меньше e, когда абсолютная величина разности
будет меньше e, когда абсолютная величина разности ![]() будет меньше
будет меньше ![]() , но больше нуля
, но больше нуля
![]() , если
, если ![]() при
при ![]() .
.
Таким образом, первое определение предела функции основано на понятии предела числовой последовательности, и его называют определением на «языке последовательностей». Второе определение носит название «на языке ![]() ».
».
Кроме понятия предела функции в точке, существует также понятие предела функции при стремлении аргумента к бесконечности: число А называется пределом функции ![]() при
при ![]() , если для любого числа
, если для любого числа ![]() существует такое число d, что при всех
существует такое число d, что при всех ![]() справедливо неравенство
справедливо неравенство ![]() :
: ![]() .
.
Теоремы о пределах функций
являются базой для общих правил нахождения пределов функций. Можно показать, что арифметические операции над функциями, имеющими предел в точке ![]() , приводят к функциям, также имеющим предел в этой точке.
, приводят к функциям, также имеющим предел в этой точке.
Примеры
Найти предел функции ![]()
Решение: Имеем неопределенность вида ![]() . Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель
. Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель ![]() , который при
, который при ![]() не равен нулю. В результате неопределенность будет раскрыта.
не равен нулю. В результате неопределенность будет раскрыта.
![]()
Пусть функция ![]() определена в некоторой окрестности точки
определена в некоторой окрестности точки ![]() .
.
Производной функции ![]() в точке
в точке ![]() называется предел
отношения
называется предел
отношения ![]() , когда
, когда ![]() (если этот предел существует). Производная функции
(если этот предел существует). Производная функции ![]() в точке
в точке ![]() обозначается
обозначается
![]() .
.
Например, выражение ![]() следует понимать как производную функции
следует понимать как производную функции ![]() в точке
в точке ![]() .
.
Определение производной можно записать в виде формулы
![]() . (4.1)
. (4.1)
Предел (4.1) может не существовать. В этом случае говорят, что функция ![]() не имеет производной в точке
не имеет производной в точке ![]() . Если предел (4.1) равен
. Если предел (4.1) равен ![]() , то говорят, что функция
, то говорят, что функция ![]() имеет в точке
имеет в точке ![]() бесконечную производную.
бесконечную производную.
В различных задачах (в том числе и экономических) производная функции ![]() интерпретируется как скорость изменения величины y относительно x. Геометрический смысл производной состоит в том, что
интерпретируется как скорость изменения величины y относительно x. Геометрический смысл производной состоит в том, что ![]() – это тангенс угла наклона касательной к графику
– это тангенс угла наклона касательной к графику ![]() в точке
в точке ![]() .
.
Нахождение производной функции называется дифференцированием этой функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке.
Укажем правила дифференцирования, которые сводят вычисление производных одних функций к вычислению производных других (более простых) функций.
Если функции ![]() дифференцируемы в точке
дифференцируемы в точке ![]() , то сумма, разность, произведение и частное этих функций также дифференцируемы в точке
, то сумма, разность, произведение и частное этих функций также дифференцируемы в точке ![]() , и справедливы следующие формулы
, и справедливы следующие формулы
![]() .
.
Если функция ![]() имеет обратную функцию
имеет обратную функцию ![]() и в точке
и в точке ![]() производная
производная ![]() , то обратная функция
, то обратная функция ![]() дифференцируема в точке
дифференцируема в точке ![]() и
и ![]() или
или ![]() .
.
Если функция ![]() дифференцируема в точке
дифференцируема в точке ![]() и
и ![]() , то сложная функция
, то сложная функция ![]() также дифференцируема в
также дифференцируема в ![]() и верна следующая формула
и верна следующая формула
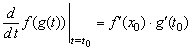 или
или ![]() .
.
Пример.
Найти производную функции ![]()
Решение:
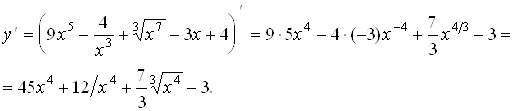
Функция ![]() , определенная во всех точках промежутка
, определенная во всех точках промежутка ![]() , называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т. е,
, называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т. е,
если ![]() то при
то при
![]() – возрастающая,
– возрастающая, ![]() – убывающая.
– убывающая.
Из данного определения вытекает, что для возрастающей функции приращения аргумента и функции имеет один и тот же знак, в силу чего их отношение положительно: ![]() . Для убывающей функции эти приращения имеют разные знаки, в силу чего
. Для убывающей функции эти приращения имеют разные знаки, в силу чего ![]() . Те значения аргумента, при которых функция достигает своих наибольших и наименьших по сравнению с близкими значений, называются точками максимума и минимума (точками экстремума).
. Те значения аргумента, при которых функция достигает своих наибольших и наименьших по сравнению с близкими значений, называются точками максимума и минимума (точками экстремума).
Точка ![]() называется точкой максимума (минимума) непрерывной функции
называется точкой максимума (минимума) непрерывной функции ![]() , а значение
, а значение ![]() называется максимумом (минимумом) этой функции, если существует некоторая окрестность точки
называется максимумом (минимумом) этой функции, если существует некоторая окрестность точки ![]() такая, что значение функции в любой точке этой окрестности будет меньше (больше), чем ее значение в самой точке
такая, что значение функции в любой точке этой окрестности будет меньше (больше), чем ее значение в самой точке ![]() , т. е. меньше (больше), чем максимум (минимум)
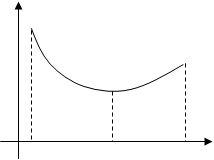
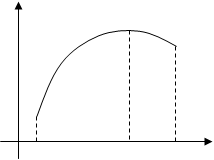
, т. е. меньше (больше), чем максимум (минимум) ![]() (рис. 1).
(рис. 1).
 у
max у
у
max у
min
f(х0) f(х0)
О х0–d х0 х0+d х О х0–d х0 х0+d х
| точка максимума | точка минимума |
Рис. 1
Из определений точек экстремума следует, что вне d-окрестности точки экстремума поведение функции произвольно, т. е. понятия максимума и минимума функции носят характер локальных (местных), а не абсолютных понятий.
Чтобы установить признаки возрастания и убывания и признаки экстремума функций, рассмотрим ряд важных теорем математического анализа, на которые опираются все дальнейшие исследования функций.
Рекомендуется исследование функций проводить в определенной последовательности.
1. Найти область определения функции; точки разрыва и их характер; вертикальные асимптоты графика.
2. Определить возможный тип симметрии функции (четность, нечетность функции); точки пересечения графика функции с осями координат, т. е. решить уравнения ![]() и
и ![]() .
.
3. Найти наклонные и горизонтальные асимптоты графика функции.
4. Использовать первую производную для определения области возрастания и убывания и экстремумов функции.
5. Использовать вторую производную для определения участков выпуклости и вогнутости графика и точек перегиба.
6. Построить график функции с учетом проведенного исследования.
Пример. Провести полное исследование функции
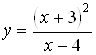
Решение:
Проведем полное исследование функции, используя следующую схему:
найти область определения функции; исследовать на четность и нечетность функцию; найти точки разрыва функции; найти асимптоты (вертикальные, наклонные и горизонтальные) графика функции; найти точки пересечения графика функции с координатными осями; исследовать функцию на монотонность (указав интервалы возрастания и убывания) и экстремум; определить интервалы выпуклости и вогнутости графика функции, точки перегиба; при необходимости вычислить значения функции в дополнительных точках; построить схематично график функции, используя результаты полученные в пунктах 1-8.Областью определения функции является множество ![]() .
.
Так как 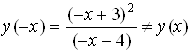 и
и ![]() , то функция не является ни четной, ни нечетной.
, то функция не является ни четной, ни нечетной.
Функция претерпевает разрыв в точке ![]() .
.
Найдем асимптоты графиков функции:
а). Прямая ![]() является вертикальной асимптотой, т.к.
является вертикальной асимптотой, т.к.
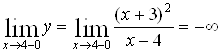 ,
, 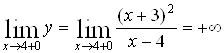
б). Находим наклонные и горизонтальные асимптоты (горизонтальные асимптоты являются частным случаем наклонных асимптот) ![]() ,
,
где  ;
;

Таким образом, прямая ![]() является единственной наклонной асимптотой и на
является единственной наклонной асимптотой и на ![]() , и на
, и на ![]() .
.
Найдем точки пересечения графика функции с осями координат.
а) С осью ![]() :
: ![]() ,
, ![]() , т.е. точка пересечения с осью
, т.е. точка пересечения с осью ![]() -
- 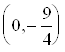 .
.
б) С осью ![]() :
: ![]() ,
, 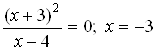 , т.е. точка пересечения с осью
, т.е. точка пересечения с осью ![]() -
- ![]() .
.
Похожие работы
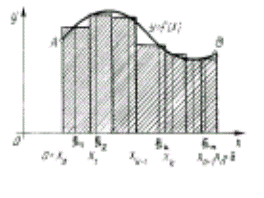
... дробей m и n; 2) если Z, то используется подстановка: a+bxn=ts, где s – знаменатель дроби 3) если Z, то применяется подстановка: ax-n+b=ts, где s – знаменатель дроби 9. Понятие определенного интеграла, его геометрический смысл. Определение. Если существует конечный передел интегральной суммы (8) - (8) при λ→0, не зависящий от способа разбиения &# ...
... элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций. Из определения 2 следует: 1.Производная от неопределенного интеграла равна подынтегральной функции, т.е.если F′ (x)= f(x), то и (∫ f(x)dx)′= (F(x)+C)′=f(x). (4) Последнее равенство нужно понимать в том смысле, что ...
... по алгебре и началам анализа, при подготовке к государственной итоговой аттестации, внешнему независимому оцениванию. Достаточно большое число задач раскрывают потенциальные возможности анализа бесконечно малых величин. 1. Производная и ее применение для решения прикладных задач 1.1 Исторические сведения Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у ...
... в потенциальную, и обратно. Но на рубеже 17-18 веков никто не догадался, что именно законы сохранения составляют следующий по глубине слой природных закономерностей. Их понимание потребовало новой революции в математике: изучения природных симметрий с помощью теории групп. Ее создание и применение заняло весь 19 век и большую часть 20 века. Предугадать такое развитие математики Ньютон не мог - ...
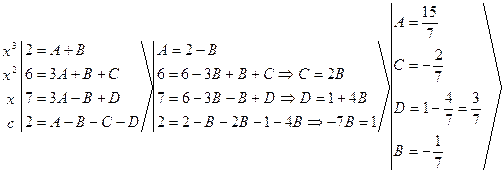
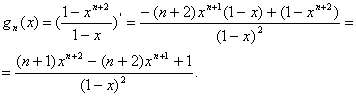
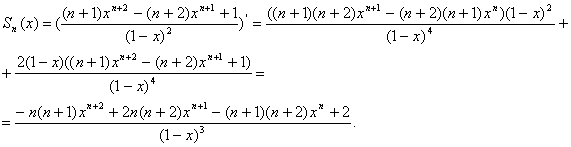
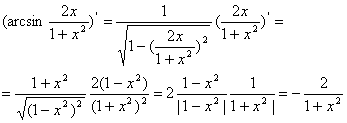

0 комментариев