Навигация
Строим в ПСК хОа графики функций
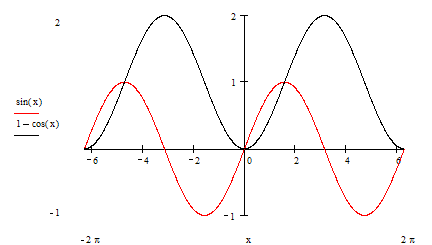
3. Строим в ПСК хОа графики функций
![]()
и нумеруем образовавшиеся области (оси роли не играют). Получилось девять областей.
4. Ищем, какая из областей подходит для данного неравенства, для чего берем точку из области и подставляем в неравенство.
Для наглядности составим таблицу.
| ? | точка | неравенство: | вывод |
| 1 |
|
| - |
| 2 |
|
| + |
| 3 |
|
| - |
| 4 |
|
| + |
| 5 |
|
| - |
| 6 |
|
| + |
| 7 |
|
| - |
| 8 |
|
| + |
| 9 |
|
| - |
5. Найдем точки пересечения графиков
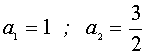
6. Зададим прямую а=сonst и будем сдвигать её от -¥ до +¥ .
Ответ.
при ![]()
![]()
при ![]()
![]()
при ![]()
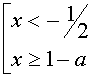
при ![]() решений нет
решений нет
при ![]()
![]()
Похожие работы
... b, c, …, k и подставить их в уравнение (1), то получим уравнение относительно x, т.е. уравнение с одним неизвестным. Переменные a, b, c, …, k, которые при решении уравнения считаются постоянными, называются параметрами, а само уравнение называется уравнением, содержащим параметры. Параметры обозначаются первыми буквами латинского алфавита: a, b, c, d, …, k, l, m, n а неизвестные – буквами x, y,z. ...
... параметра на результат. · найдём абсциссы точек пересечения графиков. · зададим прямую а=соnst и будем сдвигать её от -¥ до+¥ 7. Записываем ответ. Это всего лишь один из алгоритмов решения неравенств с параметрами, с использованием системы координат хОа. Возможны и другие методы решения, с использованием стандартной системы координат хОy. §3. Примеры I. Для всех ...
... точек координатной оси. Занятие № 4. Тема: Аналитический метод. Метод «ветвлений». Цель занятия: познакомить учеников с основным методом решения уравнений, содержащих параметр. Литература для учителя: см. [1] , [5], [6], [7], [14] Литература для ученика: см. [3] Краткое содержание: рассмотрение различных значений, принимаемых параметром. Упрощение уравнения и приведение уравнения к произведению ...
... это уравнение будем по принципу решения предыдущего. Сначала построим графики(См. рисунок 6)функций: y=tg2x u y=-tgx. По графику видно что уравнение имеет 2 решения: х=πп, пЄZ u x=2πk/3, где kЄZ.(Проверить это вычислениями) Применение графиков в решении неравенств. 1)Неравенства с модулем. Пример1. Решить неравенство |x-1|+|x+1|<4. На интеграле(-1;-∞) по ...
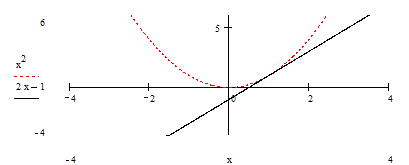
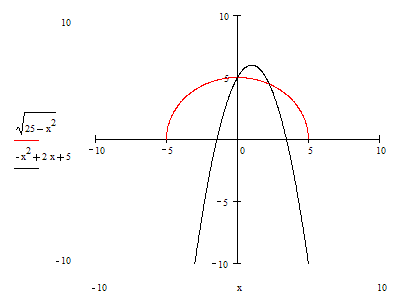
0 комментариев