Навигация
Решение некоторых уравнений и неравенств с параметром
Графическое решение уравнений, неравенств, систем с параметром.
(алгебра и начала анализа)
Исполнитель: Зырянов Р.Б.
Руководитель: Попова Н.Б.
Екатеринбург 1998
Оглавление
I. Введение
II. Уравнения с параметрами.
§1. Определения.
§2. Алгоритм решения.
§3. Примеры.
III. Неравенства с параметрами.
§1. Определения.
§2. Алгоритм решения.
§3. Примеры.
IV. Список литературы.
V. Приложения.
Введение
Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Некоторые Вузы также включают в экзаменационные билеты уравнения, неравенства и их системы, которые часто бывают весьма сложными и требующими нестандартного подхода к решению. В школе же этот один из наиболее трудных разделов школьного курса математики рассматривается только на немногочисленных факультативных занятиях.
Готовя данную работу, я ставил цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. На мой взгляд графический метод является удобным и быстрым способом решения уравнений и неравенств с параметрами.
В моём реферате рассмотрены часто встречающиеся типы уравнений, неравенств и их систем, и, я надеюсь, что знания, полученные мной в процессе работы, помогут мне при сдаче школьных экзаменов и при поступлении а ВУЗ.
§1. Основные определения
Рассмотрим уравнение
¦(a, b, c, …, k, x)=j(a, b, c, …, k, x), (1)
где a, b, c, …, k, x -переменные величины.
Любая система значений переменных
а = а0, b = b0, c = c0, …, k = k0, x = x0,
при которой и левая и правая части этого уравнения принимают действительные значения, называется системой допустимых значений переменных a, b, c, …, k, x. Пусть А – множество всех допустимых значений а, B – множество всех допустимых значений b, и т.д., Х – множество всех допустимых значений х, т.е. аÎА, bÎB, …, xÎX. Если у каждого из множеств A, B, C, …, K выбрать и зафиксировать соответственно по одному значению a, b, c, …, k и подставить их в уравнение (1), то получим уравнение относительно x, т.е. уравнение с одним неизвестным.
Переменные a, b, c, …, k, которые при решении уравнения считаются постоянными, называются параметрами, а само уравнение называется уравнением, содержащим параметры.
Параметры обозначаются первыми буквами латинского алфавита: a, b, c, d, …, k, l, m, n а неизвестные – буквами x, y,z.
Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.
Два уравнения, содержащие одни и те же параметры, называются равносильными, если:
а) они имеют смысл при одних и тех же значениях параметров;
б) каждое решение первого уравнения является решением второго и наоборот.
§2. Алгоритм решения.
Находим область определения уравнения.
Выражаем a как функцию от х.
В системе координат хОа строим график функции а=¦(х) для тех значений х, которые входят в область определения данного уравнения.
Находим точки пересечения прямой а=с, где сÎ(-¥;+¥) с графиком функции а=¦(х).Если прямая а=с пересекает график а=¦(х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение а=¦(х) относительно х.
Записываем ответ.
§3. Примеры
I. Решить уравнение
![]() (1)
(1)
Решение.
Поскольку х=0 не является корнем уравнения, то можно разрешить уравнение относительно а :
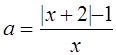 или
или 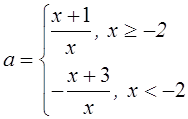
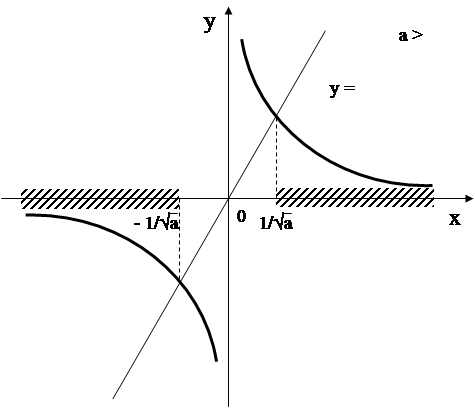
График функции – две “склеенных” гиперболы. Количество решений исходного уравнения определяется количеством точек пересечения построенной линии и прямой у=а.
Если а Î (-¥;-1]È(1;+¥)È![]() , то прямая у=а пересекает график уравнения (1) в одной точке. Абсциссу этой точки найдем при решении уравнения
, то прямая у=а пересекает график уравнения (1) в одной точке. Абсциссу этой точки найдем при решении уравнения 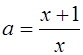 относительно х.
относительно х.
Таким образом, на этом промежутке уравнение (1) имеет решение 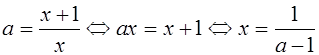 .
.
Если а Î 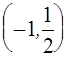 ,
то прямая у=а пересекает график уравнения (1) в двух точках. Абсциссы этих точек можно найти из уравнений
,
то прямая у=а пересекает график уравнения (1) в двух точках. Абсциссы этих точек можно найти из уравнений 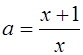 и
и 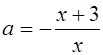 , получаем
, получаем
![]()
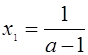 и
и 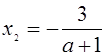 .
.
Если а Î 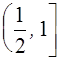 , то прямая у=а не пересекает график уравнения (1), следовательно решений нет.
, то прямая у=а не пересекает график уравнения (1), следовательно решений нет.
Ответ:
Если а Î (-¥;-1]È(1;+¥)È![]() , то
, то 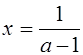 ;
;
Если а Î 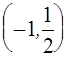 ,
то
,
то ![]()
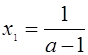 ,
, 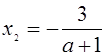 ;
;
Если а Î 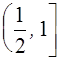 , то решений нет.
, то решений нет.
II. Найти все значения параметра а, при которых уравнение ![]() имеет три различных корня.
имеет три различных корня.
Решение.
Переписав уравнение в виде ![]() и рассмотрев пару функций
и рассмотрев пару функций ![]() , можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции
, можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции ![]() , при которых он имеет точно три точки пересечения с графиком функции
, при которых он имеет точно три точки пересечения с графиком функции ![]() .
.
В системе координат хОу построим график функции ![]() ). Для этого можно представить её в виде
). Для этого можно представить её в виде ![]() и, рассмотрев четыре возникающих случая, запишем эту функцию в виде
и, рассмотрев четыре возникающих случая, запишем эту функцию в виде
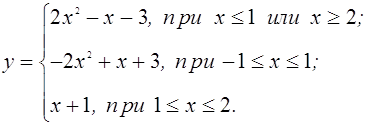
Поскольку график функции ![]() – это прямая, имеющая угол наклона к оси Ох, равный
– это прямая, имеющая угол наклона к оси Ох, равный ![]() , и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции
, и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции ![]() . Поэтому находим производную
. Поэтому находим производную ![]()
Ответ: ![]() .
.
III. Найти все значения параметра а, при каждом из которых система уравнений
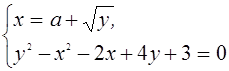
имеет решения.
Решение.
Из первого уравнения системы получим ![]() при
при ![]() Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы
Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы ![]() “скользят” вершинами по оси абсцисс.
“скользят” вершинами по оси абсцисс.
Выделим в левой части второго уравнения полные квадраты и разложим её на множители
![]()
Множеством точек плоскости ![]() , удовлетворяющих второму уравнению, являются две прямые
, удовлетворяющих второму уравнению, являются две прямые
![]() и
и ![]()
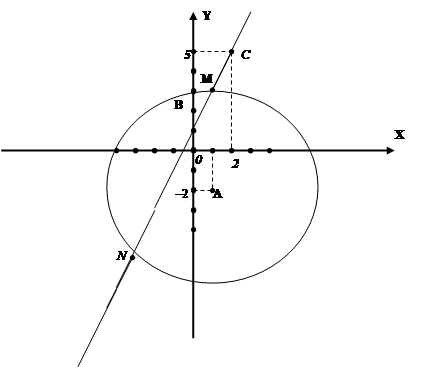
Выясним, при каких значениях параметра а кривая из семейства “полупарабол” имеет хотя бы одну общую точку с одной из полученных прямых.
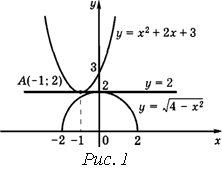
Если вершины полупарабол находятся правее точки А, но левее точки В (точка В соответствует вершине той “полупараболы”, которая касается
прямой ![]() ), то рассматриваемые графики не имеют общих точек. Если вершина “полупараболы” совпадает с точкой А, то
), то рассматриваемые графики не имеют общих точек. Если вершина “полупараболы” совпадает с точкой А, то ![]() .
.
Случай касания “полупараболы” с прямой ![]() определим из условия существования единственного решения системы
определим из условия существования единственного решения системы

В этом случае уравнение
![]()
имеет один корень, откуда находим :
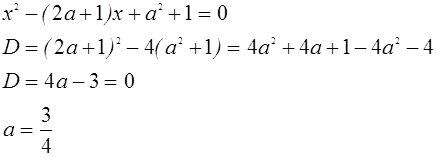
Следовательно, исходная система не имеет решений при ![]() , а при
, а при ![]() или
или ![]() имеет хотя бы одно решение.
имеет хотя бы одно решение.
Ответ: а Î (-¥;-3] È(![]() ;+¥).
;+¥).
IV. Решить уравнение
![]()
Решение.
Использовав равенство ![]() , заданное уравнение перепишем в виде
, заданное уравнение перепишем в виде
![]()
Это уравнение равносильно системе
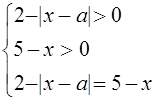
Уравнение ![]() перепишем в виде
перепишем в виде
![]() .
(*)
.
(*)
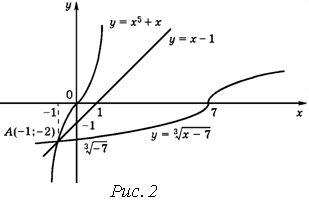
Последнее уравнение проще всего решить, используя геометрические соображения. Построим графики функций ![]() и
и ![]() Из графика следует, что при
Из графика следует, что при ![]() графики не пересекаются и, следовательно, уравнение не имеет решений.
графики не пересекаются и, следовательно, уравнение не имеет решений.
Если ![]() , то при
, то при ![]() графики функций совпадают и, следовательно, все значения
графики функций совпадают и, следовательно, все значения ![]() являются решениями уравнения (*).
являются решениями уравнения (*).
При ![]() графики пересекаются в одной точке, абсцисса которой
графики пересекаются в одной точке, абсцисса которой 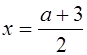 . Таким образом, при
. Таким образом, при ![]() уравнение (*) имеет единственное решение -
уравнение (*) имеет единственное решение - 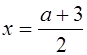 .
.
Исследуем теперь, при каких значениях а найденные решения уравнения (*) будут удовлетворять условиям
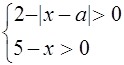
Пусть ![]() , тогда
, тогда ![]() . Система примет вид
. Система примет вид
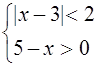
Её решением будет промежуток хÎ (1;5). Учитывая, что ![]() , можно заключить, что при
, можно заключить, что при ![]() исходному уравнению удовлетворяют все значения х из промежутка [3; 5).
исходному уравнению удовлетворяют все значения х из промежутка [3; 5).
Рассмотрим случай, когда 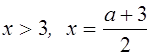 . Система неравенств примет вид
. Система неравенств примет вид
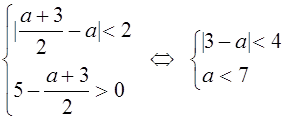
Решив эту систему, найдем аÎ (-1;7). Но ![]() , поэтому при аÎ (3;7) исходное уравнение имеет единственное решение
, поэтому при аÎ (3;7) исходное уравнение имеет единственное решение 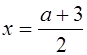 .
.
Ответ:
если аÎ (-¥;3), то решений нет;
если а=3, то хÎ [3;5);
если aÎ (3;7), то 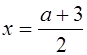 ;
;
если aÎ [7;+¥), то решений нет.
V. Решить уравнение
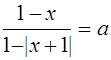 , где а - параметр. (5)
, где а - параметр. (5)
Решение.
1. При любом а : ![]()
2. Если ![]() , то
, то 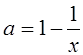 ;
;
если ![]() , то
, то 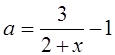 .
.
3. Строим график функции 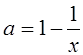 , выделяем ту его часть , которая соответствует
, выделяем ту его часть , которая соответствует ![]() . Затем отметим ту часть графика функции
. Затем отметим ту часть графика функции 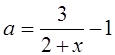 , которая соответствует
, которая соответствует ![]() .
.
Похожие работы
... список или выбрать из 2-3 текстов наиболее интересные места. Таким образом, мы рассмотрели общие положения по созданию и проведению элективных курсов, которые будут учтены при разработке элективного курса по алгебре для 9 класса «Квадратные уравнения и неравенства с параметром». Глава II. Методика проведения элективного курса «Квадратные уравнения и неравенства с параметром» 1.1. Общие ...
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
... ;[0; 1), тогда x – x +1 = 1; 1 = 1 Þ x — любое число из [0; 1). В) x Î[1; ¥), тогда x + x – 1 = 1; 2x = 2; x = 1 Î[1; ¥). Ответ: x Î[0; 1]. Основные методы решения рациональных уравнений. 1) Простейшие: решаются путём обычных упрощений — приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax2 + bx + c = 0 решаются по ...
... функция является знакопостоянной. Вычисляя, например, , получаем, что функция принимает только положительные значения. Ответ. . Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих ...
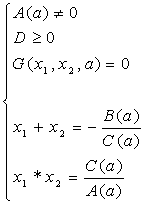
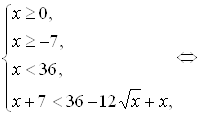
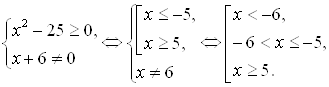
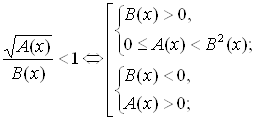
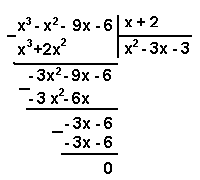


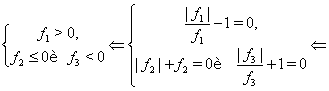
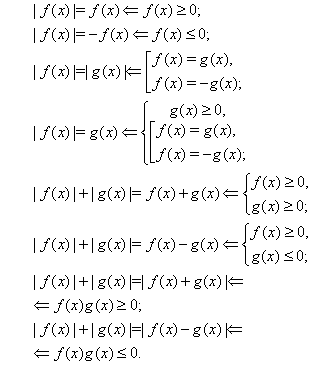
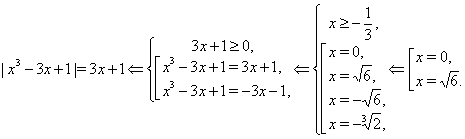
0 комментариев