Навигация
Построим графики частотных характеристик.Для этого сначала получим их численные значения
33175
знаков
0
таблиц
0
изображений
7. Построим графики частотных характеристик.Для этого сначала получим их численные значения.
4.3.1.ДИФФЕРЕНЦИРУЮЩЕЕ ИДЕАЛЬНОЕ ЗВЕНО
1. Данное звено описывается следующим уравнением:
aoy(t)=b1
(1)
Коэффициенты имеют следующие значения:
ao=2
b1=4
Запишем это уравнение в стандартной форме. Для этого разделим (1) на ao:
y(t)=
y(t)=k (2),
где k=
-коэффициент передачи.
Запишем исходное уравнение в операторной форме, используя подстановку p=
.Получим:
y(t)=kpg(t) (3)
2. Получим передаточную функцию для идеального звена. Воспользуемся преобразованиями Лапласа:
y(t)=Y(s)
g(t)=G(s)
=sG(s)
По определению передаточная функция находится как отношение выходного сигнала к входному. Тогда уравнение (2) будет иметь вид:
Y(s)=ksG(s)
W(s)=ks (4)
3. Найдем выражения для переходной функции и функции веса из преобразлваний Лапласа,т.е.
h(t)=H(s)
H(s)=W(s)
=k
Переходя к оригиналу, получим
h(t)=kЧ d (t) (5)
Функцию веса можно получить по преобразованию Лапласа из передаточной функции:
w(t)=w(s)
w(s)=W(s)Ч 1=ks
Переходя к оригиналу, получим
w(t)=k
(6)
4. Построим графики переходной функции и функции веса. Подставляя исходные данные, вычислим коэффициент передачи и временные характеристики:
5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw :
W(s)=ks
W(jw )=jkw (7)
W(jw )=U(w )+jV(w )
U(w )=0
V(w )=kw
6. Получим аналитические выражения для частотных характеристик. По определению амплитудная частотная характеристика (АЧХ) - это модуль частотной передаточной функции, т.е.
A(w )=Ѕ W(jw )Ѕ
A(w )=kЅ w Ѕ (8)
Фазовая частотная характеристика (ФЧХ) - это аргумент частотной передаточной функции, т.е.
j (w )=argW(jw )
j (w )=arctgkw (9)
Для построения логарифмических частотных характеристик вычислим
L(w )=20lg A(w )
L(w )=20lgkЅ w Ѕ
7. Построим графики частотных характеристик. Для этого сначала получим их численные выражения.
4.3.2.ДИФФЕРЕНЦИРУЮЩЕЕ РЕАЛЬНОЕ ЗВЕНО
1. Данное звено описывается следующим уравнением:
a1 
+ aoy(t) =b1
(1)
Коэффициенты имеют следующие значения:
a1=1,24
ao=2
b1=4
Запишем это уравнение в стандартной форме. Для этого разделим (1) на a1:
+y(t)=
T+y(t)=k (2),
где k=-коэффициент передачи,
T1=
-постоянная времени.
Запишем исходное уравнение в операторной форме, используя подстановку p=
.Получим:
(Tp+1)y(t)=kpg(t) (3)
2. Получим передаточную функцию для апериодического звена. Воспользуемся преобразованиями Лапласа:
y(t)=Y(s)
=sY(s)
g(t)=G(s)
=sG(s)
По определению передаточная функция находится как отношение выходного сигнала к входному. Тогда уравнение (2) будет иметь вид:
TsY(s)+Y(s)=ksG(s)
W(s)=
(4)
3. Найдем выражения для переходной функции и функции веса. По определению аналитическим выражением переходной функции является решение уравнения (2) при нулевых начальных условиях, т.е. g(t)=1 или по преобразованиями Лапласа
h(t)=H(s)
H(s)=W(s)
=
=
Переходя к оригиналу, получим
h(t)=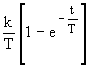
Ч 1(t) (5)
Функцию веса можно получить из преобразований Лапласа
w(t)=w(s)
w(s)=W(s)Ч 1
W(s)= 
=
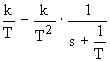
Переходя к оригиналу, получим
w(t)=
Ч d (t)
e
Ч 1(t) (6)
4. Построим графики переходной функции и функции веса. Подставляя исходные данные, вычислим коэффициент передачи, постоянные времени и временные характеристики:
5. Получим частотную передаточную функцию, заменив в передаточной функции (4) s на jw :
W(s)=
W(jw )=
W(jw )=
=
6.Найдем АЧХ:
A(w )=Ѕ W(jw )Ѕ
A(w )=
=
Найдем ФЧХ:
j (w )=argW(jw )
j (w )=arctgkw -arctgTw
L(w )=20lgA(w )
L(w )=20lg
4.3.3.ФОРСИРУЮЩЕЕ ЗВЕНО 1-го ПОРЯДКА
Данное звено описывается следующим уравнением:
a0y(t)=b1
+b0g(t)
y(t)=
+
g(t)
k1=
k=
p=
y(t)=k1pg(t)+kg(t)
y(t)=Y(s)
g(t)=G(s)
Y(s)=k1sG(s)+kG(s)
W(s)=k1s+k
H(s)=
=k1+
h(t)=k1d (t)+k1(t)
W(jw )=k1jw +k
U(w )=k
V(w )=k1w
A(w )=Ѕ W(jw )Ѕ
A(w )=
j (w )=argW(jw )
j (w )=arctg
L(w )=20lgA(w )
L(w )=20lg
4.3.4.ФОРСИРУЮЩЕЕ ЗВЕНО 2-го ПОРЯДКА
a0y(t)=b2
+b1+b0g(t)
y(t)=
+
+
g(t)
y(t)=k2
+k1+kg(t)
y(t)=k2p2g(t)+k1pg(t)+kg(t)
Y(s)=(k2s2+k1s+k)G(s)
W(s)=k2s2+k1s+k
H(s)=k2s+k1+
h(t)=k2
+k1d (t)+k11(t)
w(s)=W(s)=k2s2+k1s+k
w(t)=k2
+k1+kd (t)
W(jw )=k1jw +k - k2w 2
U(w )=k - k2w 2
V(w )=k1jw
A(w )=
j (w )=arctg
L(w )=20lg
Похожие работы
... условий: y(x0)=y0, . Эти начальные условия дают соответственно n уравнений , , , ……………………………… , решая которые относительно c1, c2 , …, cn находят значения этих постоянных. Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0). Геометрическая ...
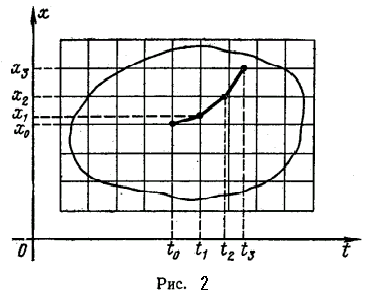
... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...
... его тождество. Общим решением дифференциального уравнения го порядка называется такое его решение , которое является функцией переменных и произвольных независимых постоянных . Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных . Теорема. Пусть в дифференциальном уравнении (1) функция ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
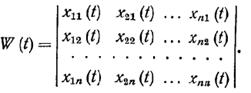
0 комментариев