Навигация
Разностные аппроксимации
Различные способы приближенной замены одномерных дифференциальных уравнений разностными изучались ранее. Напомним примеры разностных аппроксимаций и введем необходимые обозначения. Будем рассматривать равномерную сетку с шагом h, т.е. множество точек
w h={xi=ih, i=0, ± 1, ± 2,…}.
![]() Пусть u(x) – достаточно гладкая функция, заданная на отрезке [xi-1, xi+1]. Обозначим
Пусть u(x) – достаточно гладкая функция, заданная на отрезке [xi-1, xi+1]. Обозначим
Разностные отношения
называются соответственно правой, левой и центральной разностными производными функции u(x) в точке xi , т.е. при фиксированном xi и при h® 0 (тем самым при i® Ґ ) пределом этих отношений является u’(xi). Проводя разложение по формуле Тейлора, получим
ux,i – u’(xi) = 0,5hu’’(xi) + O(h2),
ux,i – u’(xi) = -0,5hu’’(xi) + O(h2),
ux,i – u’(xi) = O(h2),
Отсюда видно, что левая и правая разностные производные аппроксимируют u’(x) с первым порядком по h, а центральная разностная производная – со вторым порядком. Нетрудно показать, что вторая разностная производная
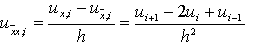
аппроксимирует u’’(xi) со вторым порядком по h, причем справедливо разложение
![]()
Рассмотрим дифференциальное выражение
![]() (1)
(1)
с переменным коэффициентом k(x). Заменим выражение (1) разностным отношением
![]() (2)
(2)
где a=a(x) – функция, определенная на сетке w h. Найдем условия, которым должна удовлетворять функция a(x) для того, чтобы отношение (aux)x,i аппроксимировало (ku’)’ в точке xi со вторым порядком по h. Подставляя в (2) разложения
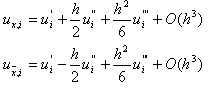
где ui’ = u’(xi), получим![]()
С другой стороны, Lu = (ku’)’ = ku’’ + k’u’,
т.е.![]()
Отсюда видно, что Lhu–Lu = O(h2), если выполнены условия
![]() (3)
(3)
Условия (3) называются достаточными условиями второго порядка аппроксимации. При их выводе предполагалось, что функция u(x) имеет непрерывную четвертую производную и k(x) – дифференцируемая функция. Нетрудно показать, что условиям (3) удовлетворяют, например, следующие функции:
![]()
Заметим, что если положить ai = k(xi), то получим только первый порядок аппроксимации.
В качестве следующего примера рассмотрим разностную аппроксимацию оператора Лапласа
![]() (4)
(4)
Введем на плоскости (x1, x2) прямоугольную сетку с шагом h1 по направлению x1 и с шагом h2 по направлению x2, т.е. множество точек
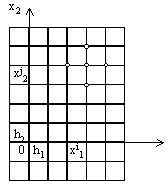
w h = {(xi1, xj2) | xi1 = ih1, xj2 = jh2; i, j = 0, ± 1, ± 2,…},
и обозначим
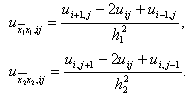
Из предыдущих рассуждений следует, что разностное выражение
![]() (5)
(5)
аппроксимирует дифференциальное выражение (4) со вторым порядком, т.е. Lhuij – Lu(xi1, xj2) = O(h21) + O(h22). Более того, для функций u(x1, x2), обладающих непрерывными шестыми производными, справедливо разложение
![]()
Разностное выражение (5) называется пятиточечным разностным оператором Лапласа, так как оно содержит значения функции u(x1, x2) в пяти точках сетки, а именно в точках (x1i, x2j), (x1i± 1, x2j), (x1i, x2 j± 1). Указанное множество точек называется шаблоном разностного оператора. Возможны разностные аппроксимации оператора Лапласа и на шаблонах, содержащих большее число точек.
2. Исследование аппроксимации и сходимости 2.1. Аппроксимация дифференциального уравнения.Ранее рассматривалась краевая задача
(k(x) u’(x))’ – q(x) u(x) + f(x) = 0, 0 < x < l,(1)
– k(0) u’(0) + b u(0) = m 1, u(l) = m 2,(2)
k(x) і c1 > 0, b і 0,
для которой интегро-интерполяционным методом была построена разностная схема
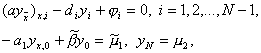 (3), (4)
(3), (4)
где
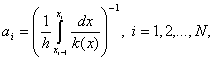
(5)
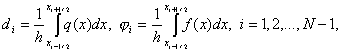
(6)
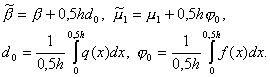
Обозначим через Lu(x) левую часть уравнения (1) и через Lhyi – левую часть уравнения (3), т.е.
![]()
Пусть u (x) – достаточно гладкая функция и u (xi) – ее значение в точке xi сетки
w h = {xi = ih, i = 0, 1, …,N, hN = l}(7)
Говорят, что разностный оператор Lh аппроксимирует дифференциальный оператор L в точке x=xi, если разность Lhu i – Lhu (xi) стремится к нулю при h® 0. В этом случае говорят также, что разностное уравнение (3) аппроксимирует дифференциальное уравнение (1).
Чтобы установить наличие аппроксимации, достаточно разложить по формуле Тейлора в точке x=xi значения u i± 1 = u (xi ± h), входящие в разностное выражение Lhu i. Большая часть этой работы проделана в предыдущей главе, где показано, что при условиях
![]() (8)
(8)
выполняется соотношение
![]()
Если кроме того, докажем, что
di = q(xi) + O(h2), j i = f(xi) + O(h2)(9)
то тем самым будет установлено, что оператор Lh аппроксимирует L со вторым порядком по h, т.е.
Lhu i – Lu (xi) = O(h2), i = 1, 2,…, N–1(10)
Итак, доказательство второго порядка аппроксимации сводится к проверке сводится к проверке условий (8), (9) для коэффициентов (5), (6). Проверим сначала выполнение условий (8). Обозначая p(x) = k-1(x), получим
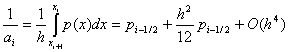
следовательно,
![]()
Аналогично
![]()
Отсюда получим
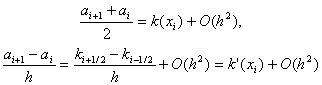
т.е. условия (8) выполнены. Условия (9) выполнены в силу того, что замена интегралов (6) значениями qi, fi соответствует приближенному вычислению этих интегралов по формуле прямоугольников с узлом в середине отрезка интегрирования.
2.2. Аппроксимация граничного условия.Исследуем погрешность аппроксимации разностного граничного условия (4). Обозначим lhu (0) = –a1u x, 0 + b u 0. Если u (x) – произвольная достаточно гладкая функция, то очевидно
lhu (0) = –k(0) u ’(0) + b u (0) + O(h),
т.е. имеет место аппроксимация первого порядка по h. Однако если u =u(x) – решение задачи (1), (2), то разностное граничное условие (4) имеет второй порядок аппроксимации, т.е.
![]()
Докажем последнее утверждение. Используя разложение
ux, 0 = (u1 – u0)/h = u’(x1/2) + O(h2), x1/2 = 0,5h,
a1 = k1/2 + O(h2)
получим
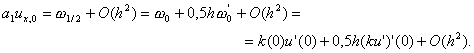
Отсюда имеем
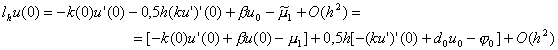
Учитывая граничное условие (2), получаем
lhu(0) = 0,5h [– (ku’)’(0) + d0u0 – j 0] + O(h2).
Выражение, стоящее в квадратных скобках, преобразуем, учитывая уравнение (1), к виду
– (ku’)’(0) + d0u0 – j 0 = – (ku’)’(0) + q(0)u(0) – f(0) +
+ (d0 – q(0))u0 – (f(0) – j 0) = (d0 – q(0))u0 – (f(0) – j 0).
Из соотношений
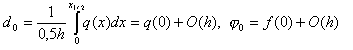
получаем
![]()
что и требовалось доказать.
Таким образом, при достаточной гладкости коэффициентов k(x), q(x), f(x) и решения u(x) разностная схема (10) аппроксимирует исходную задачу (2) со вторым порядком по h.
При практическом использовании разностной схемы для нахождения ее коэффициентов не обязательно вычислять интегралы (4), (6) точно. Можно воспользоваться коэффициентами, полученными путем замены этих интегралов квадратурными формулами, имеющими точность O(h2) и выше. Например, в результате применения формулы прямоугольников получим следующие коэффициенты: ai = k(xi – 0,5h), di = q(xi), j i = f(xi).
Применяя формулу трапеций, получим
![]()
Представление коэффициентов разностной схемы в виде интегралов (4), (6) оказывается полезным при исследовании сходимости в случае разрывных функций k(x), q(x), f(x).
2.3. Уравнение для погрешности.Решение yi = y(xi) разностной задачи (3), (4) зависит от шага h сетки, y(xi) = yh(xi). По существу, мы имеем семейство решений {yh(xi)}, зависящее от параметра h. Говорят, что решение yh(x) разностной задачи сходится к решению u(x) исходной дифференциальной задачи, если при h® 0 погрешность yh(xi) – u(xi), i = 0, 1,…, N, стремится к нулю в некоторой норме. В настоящем параграфе в качестве такой нормы будем брать норму в сеточном пространстве C(w h), т.е. положим
![]()
Говорят, что разностная схема имеет m-й порядок точности (или сходится с порядком m), если
![]()
где m>0, M>0 – константы, не зависящие от h.
Выше было установлено, что схема (3), (4) имеет второй порядок аппроксимации. Докажем теперь, что эта схема имеет и второй порядок точности. Для этого прежде всего выпишем уравнение, которому удовлетворяет погрешность zi = yi – u(xi). Поставим yi = zi + u(xi) в уравнения (3), (4). Тогда получим уравнения
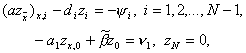 (11), (12)
(11), (12)
где обозначено
![]()
Функция y i, входящая в правую часть уравнения (11), называется погрешностью аппроксимации дифференциального уравнения (1) разностным уравнением (3) на решении задачи (1), (2). В п.1 было доказано, что y i = O(h2) при h® 0, i=1, 2,…, N–1. Аналогично, величина n 1 является по определению погрешностью аппроксимации краевого условия (2) разностным краевым условием (4) на решении задачи (1), (2), причем n 1=O(h2). Таким образом, структура уравнений для погрешности (11), (12) та же, что и у разностной схемы (3), (4), отличаются только правые части.
Чтобы доказать сходимость разностной схемы, оценим решение задачи (11), (12) через правые части y i, n 1, т.е. получим неравенство вида
![]() (13)
(13)
![]() с константой M1, не зависящей от h. Из этого неравенства и будет следовать, что
с константой M1, не зависящей от h. Из этого неравенства и будет следовать, что
Отметим, что неравенства вида (13), называемые априорными оценками, нашли широкое применение в теории разностных схем. Поскольку структура для погрешности (11), (12) та же, что и у разностной схемы (3), (4), а отличаются только правые части, то оценка (13) выполняется одновременно с аналогичной оценкой
![]()
для разностной схемы (3), (4) при m 2 = 0. Последняя оценка выражает устойчивость решения разностной задачи по правым частям j и m 1.
2.4. Разностные тождества и неравенства.Для того, чтобы доказать неравенство (13), нам потребуются некоторые разностные тождества и неравенства. Будем рассматривать сеточные функции, заданные на сетке (7). Обозначим
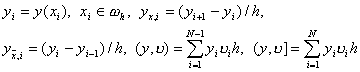
Справедливо следующее разностное утверждение:
(y, u x) = –(u , yx) + yNu N – y0u 1.(14)
Действительно,
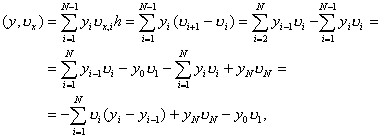
что и требовалось доказать. Тождество (14) называется формулой суммирования по частям.
Подставляя в (14) вместо u выражение azx и вместо y функцию z, получаем первую разностную формулу Грина
![]() (15)
(15)
Здесь![]()
В частности, если zN = 0 (как в задаче (11), (12)), то получим
(16)![]()
Обозначим
![]()
и докажем, что для любой сеточной функции zi, удовлетворяющей условию zN = 0, справедливо неравенство
![]() (17)
(17)
Для доказательства воспользуемся тождеством
![]()
и применим неравенство Коши-Буняковского
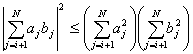
Тогда получим
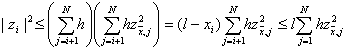
Откуда сразу следует неравенство (17).
2.5. Доказательство сходимости.Возвращаясь к доказательству сходимости схемы (3), (4), получим тождество, которому удовлетворяет погрешность zi = yi – u(xi). Для этого умножим уравнение (11) на hzi и просуммируем по i от 1 до N–1. Тогда получим
![]()
Отсюда, применяя разностную формулу Грина (16), получим
![]()
Далее, согласно (12) имеем
![]()
следовательно, справедливо тождество
![]() (18)
(18)
Из этого тождества и будет сейчас выведено требуемое неравенство вида (13).
Заметим прежде всего, что если
k(x) і c1 > 0, b і 0, q(x) і 0,
то коэффициенты разностной схемы (3), (4) удовлетворяют неравенствам
ai і c1 > 0, b і 0, di і 0.(19)
Это утверждение сразу следует из явного представления коэффициентов (5), (6).
Воспользовавшись (19), оценим слагаемые, входящие в левую часть тождества (18), следующим образом:
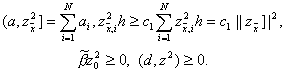
Тогда придем к неравенству
![]() (20)
(20)
Оценим сверху правую часть этого неравенства. Будем иметь
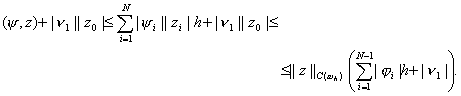
Подставляя эту оценку в (20) и учитывая неравенство (17), получим
![]()
т.е.
![]()
Окончательно
![]() (21)
(21)
![]()
Посколькуиз неравенства следует,
что погрешность zi = yi – u(xi) также является величиной O(h2) при h® 0. Итак, справедливо следующее утверждение.
Пусть k(x) – непрерывно дифференцируемая и q(x), f(x) – непрерывные функции при xО [0, l], решение u(x) задачи (1), (2) обладает непрерывными четвертыми производными. Пусть коэффициенты разностной схемы (3), (4) удовлетворяют условиям (8), (9), (19). Тогда решение разностной задачи (3), (4) сходится при h® 0 к решению исходной дифференциальной задачи (1), (2) со вторым порядком по h, так что выполняется оценка
![]()
где M – постоянная, не зависящая от h.
3. Разностные схемы для уравнения теплопроводности 3.1. Исходная задача.Будем рассматривать следующую первую краевую задачу для уравнения теплопроводности с постоянными коэффициентами. В области {0 < x < 1, 0 < t Ј T} требуется найти решение уравнения
![]() (1)
(1)
удовлетворяющее начальному условию
u(x, 0) = u0(x)(2)
и граничным условиям
u(0, t) = m 1(t), u(1, t) = m 2(t).(3)
Здесь u0(x), m 1(t), m 2(t) – заданные функции. Известно, что при определенных предположениях гладкости решение задачи (1)–(3) существует и единственно. В дальнейшем при исследовании аппроксимации разностных схем будем предполагать, что решение u(x, t) обладает необходимым по ходу изложения числом производных по x и по t. Решение задачи (1) – (3) удовлетворяет принципу максимума и тем самым непрерывно зависит от начальных и граничных данных.
3.2. Явная схема.Как всегда, для построения разностной схемы надо прежде всего ввести сетку в области изменения независимых переменных и задать шаблон, т.е. множество точек сетки, участвующих в аппроксимации дифференциального выражения. Введем сетку по переменному x такую же, как в предыдущей главе, т.е.
w h = {xi = ih, i = 0, 1,…, N, hN = 1}
и сетку по переменному t с шагом t , которую обозначим
w t = {tn = nt , n = 0, 1,…, K, Kt = T}
Точки (xi, tn), i = 0, 1,…, N, n = 0, 1,…, K, образуют узлы пространственно-временной сетки w h, t = w h x w t . Узлы (xi, tn), принадлежащие отрезкам I0 = {0 Ј x Ј 1, t = 0}, I1 = {x = 0, 0 Ј t Ј T}, I2 = {x = 1, 0 Ј t Ј T}, называются граничными узлами сетки w h, t , а остальные узлы – внутренними. На рисунке граничные узлы обозначены крестиками, а внутренние – кружочками.
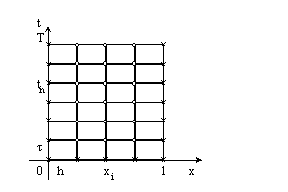
Слоем называется множество всех узлов сетки w h, t , имеющих одну и ту же временную координату. Так, n-м слоем называется множество узлов
(x0, tn), (x1, tn),…, (xN, tn).
Для функции y(x, t), определенной на сетке w h, t , введем обозначения yni = y(xi, tn),
![]() (4)
(4)
Иногда для упрощения записи индексы i и n будем опускать, обозначая ![]()
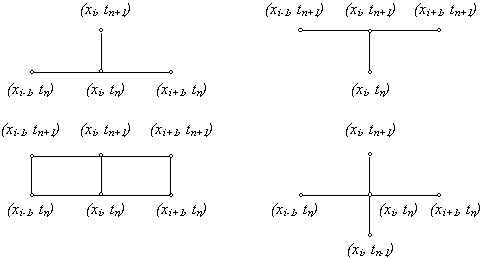
Чтобы аппроксимировать уравнение (1) в точке (xi, tn), введем шаблон, изображенный на рисунке и состоящий из четырех узлов (xi± 1, tn), (xi, tn), (xi, tn+1). Производную ¶ u/¶ t заменим в точке (xi, tn) разностным отношением ynt, i, а производную ¶ 2u/¶ 2x – второй разностной производной ynxx, i. Правую часть f(x, t) заменим приближенно сеточной функцией j ni, в качестве j ni можно взять одно из следующих выражений:
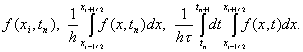
В результате получим разносное уравнение
![]() (5)
(5)
которое аппроксимирует исходное дифференциальное уравнение в точке (xi, tn) с первым порядком по t и вторым порядком по h при условии, что разность j ni – f(xi, tn) имеет тот же порядок малости.
Под разностной схемой понимается совокупность разностных уравнений, аппроксимирующих основное дифференциальное уравнение во всех внутренних узлах сетки и дополнительные (начальные и граничные) условия – в граничных узлах сетки. Разностную схему по аналогии с дифференциальной задачей будем называть также разностной задачей. В данном случае разностная схема имеет вид
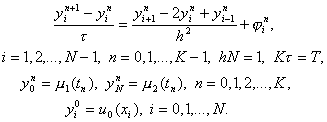 (6)
(6)
Эта схема представляет собой систему линейных алгебраических уравнений с числом уравнений, равным числу неизвестных. Находить решение такой системы следует по слоям. Решение на нулевом слое задано начальными условиями y0i = u0(xi), i = 0, 1,…, N. Если решение yni, i = 0, 1,…, N, на слое n уже найдено, то решение yin+1 на слое n+1 находится по явной формуле
![]() (7)
(7)
а значениядоопределяются из граничных![]()
условий. По этой причине схема (6) называется явной разностной схемой. Несколько позже мы познакомимся и с неявными схемами, в которых для нахождения yin+1 при заданных yin требуется решать систему уравнений.
Погрешность разностной схемы (6) определяется как разность zin = yin – u(xi, tn) между решением задачи (6) и решением исходной задачи (1) – (3). Подставляя в (6) yin = zin + u(xi, tn), получим уравнение для погрешности
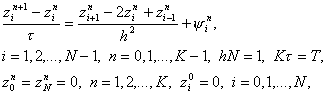 (8)
(8)
где ![]() – погрешность аппроксимации разностной
– погрешность аппроксимации разностной
схемы (6) на решении задачи (1) – (3), y in = O(t + h2). Можно оценить решение zin уравнения (8) через правую часть y in и доказать тем самым сходимость разностной схемы (6) с первым порядком по t и вторым – по h. Однако это исследование мы отложим, а сейчас на примере схемы (6) продемонстрируем один распространенный прием исследования разностных схем с постоянными коэффициентами, называемый методом гармоник. Хотя данный метод не является достаточно обоснованным, в частности не учитывает влияния граничных условий и правых частей, он позволяет легко найти необходимые условия устойчивости и сходимости разностных схем. Покажем, например, что явную схему (6) можно применять лишь при условии t Ј 0,5h2, означающем, что шаг по времени надо брать достаточно малым.
Рассмотрим уравнение
![]() (9)
(9)
т.е. однородное уравнение, соответствующее (5). Будем искать частные решения (9), имеющие вид
yjn (j ) = qneijhj ,(10)
где i – мнимая единица, j – любое действительное число и q – число, подлежащее определению. Подставляя (10) в уравнение (9) и сокращая на eijhj , получим
![]()
откуда найдем
![]()
(11) ![]()
Начальные условиясоответствующие решениям вида (10) (их называют гармониками), ограничены. Если для некоторого j множитель q станет по модулю больше единицы, то решение вида (10) будет неограниченно возрастать при n® Ґ . В этом случае разностное уравнение (9) называется неустойчивым, поскольку нарушается непрерывная зависимость его решения от начальных условий. Если же |q| Ј 1 для всех действительных j , то все решения вида (10) ограничены при любом n и разностное уравнение (9) называется устойчивым. В случае неустойчивости найти решение разностной задачи (6) по формулам (7) практически невозможно, так как погрешности (например погрешности округления), внесенные в начальный момент времени, будут неограниченно возрастать при увеличении n. Такие разностные схемы называются неустойчивыми.
Для уравнения (9) неравенство |q| Ј 1 выполняется согласно (11) при всех j тогда и только тогда, когда g Ј 0,5. Таким образом, использование схемы (6) возможно лишь при выполнении условия t Ј 0,5h2. Разностные схемы, устойчивые лишь при некотором ограничении на отношение шагов по пространству и по времени, называются условно устойчивыми. Следовательно, схема (6) возможно устойчива, причем условие устойчивости имеет вид t /h2 Ј 0,5. Условно устойчивые схемы для уравнений параболического типа используются редко, так как они накладывают слишком сильное ограничение на шаг по времени. Действительно, пусть, например, h = 10-2. Тогда шаг t не должен превосходить 0,5 * 10-4, и для того чтобы вычислить решение yjn при t = 1, надо взять число шагов по времени n = t -1 і 2 * 104, т.е. провести не менее 2 * 104 вычислений по формулам (7).
3.3. Неявные схемы.Чисто неявной разностной схемой для уравнения теплопроводности теплопроводности (схемой с опережением) называется разностная схема, использующая шаблон (xi, tn), (xi± 1, tn+1), (xi, tn+1) и имеющая вид
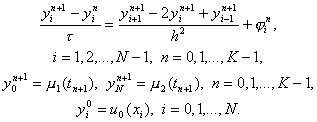 (12)
(12)
Здесь j ni = f(xi, tn+1) + O(t + h2). Схема имеет первый порядок аппроксимации по t и второй – по h. Решение системы (12) находится, как и в случае явной схемы, по слоям, начиная с n = 1. Однако, теперь, в отличие от явной схемы, для нахождения yin+1 по известным yin требуется решить систему уравнений
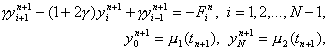 (13)
(13)
где g = t /h2, Fin = yin + t j in. Эту систему можно решать методом прогонки, так как условия устойчивости прогонки выполнены.
Для исследования устойчивости разностной схемы (12) будем искать частные решения уравнения
![]()
имеющие вид (10). Тогда получим
![]()
следовательно, |q| Ј 1 при любых j , t , h. Таким образом, схема (12) абсолютно устойчива, т.е. устойчива при любых шагах t и h. Абсолютная устойчивость является основным условием неявных схем. Теперь уже не надо брать шаг t слишком малым, можно взять, например, t = h = 10-2. Величина шагов сетки t , h определяются теперь необходимой точностью расчета, а не соображениями устойчивости.
Шеститочечной симметричной схемой называется разностная схема
(14)![]()
для которой начальные и граничные условия задаются так же, как и в схеме (12). Эта схема использует шеститочечный шаблон, изображенный на рисунке.
Обобщением трех рассмотренных схем является однопараметрическое семейство схем с весами. Зададим произвольный действительный параметр s и определим разностную схему
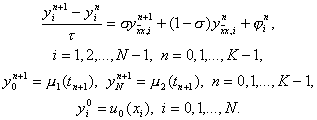 (15)
(15)
При s = 0 получим отсюда явную схему, при s = 1 – чисто неявную схему и при s = 0,5 – симметричную схему (14). Исследуем погрешность аппроксимации схемы (15) на решении исходной задачи (1) – (3). Представим решение задачи (15) в виде yin = u(xi, tn) + zin, где u(xi, tn) – точное решение дифференциальной задачи (1) – (3). Тогда для погрешности получим систему уравнений
![]() (16)
(16)
i = 1, 2,…, N – 1, n = 0, 1,…, K – 1,
z0n+1 = zNn+1 = 0, n = 0, 1,…, K – 1, zi0 = 0, i = 0, 1,…, N.
Сеточная функция y in, входящая в правую часть уравнения (16) и равная
![]() (17)
(17)
![]() называется погрешностью аппроксимации схемы (15) на решении задачи (1) – (3). Получим первые члены разложения функции y in по степеням h и t . Будем разлагать все функции, входящие в выражение для y in, по формуле Тейлора в точке (xi, tn + 0,5t ). Учитывая разложения
называется погрешностью аппроксимации схемы (15) на решении задачи (1) – (3). Получим первые члены разложения функции y in по степеням h и t . Будем разлагать все функции, входящие в выражение для y in, по формуле Тейлора в точке (xi, tn + 0,5t ). Учитывая разложения
где
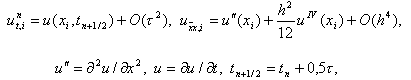
получим
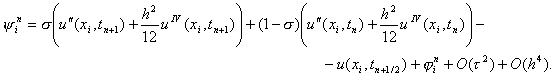
Отсюда, проводя разложение в точке (xi, tn+1/2) и обозначая u = u (xi, tn+1/2), будем иметь
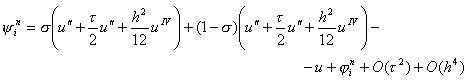
и, перегруппировывая слагаемые, получим, что
![]()
Учитывая уравнение (1) u’’ – u = – f и следствие из него uIV – u’’ = –f’’, окончательно можно записать, что
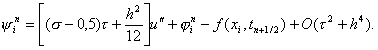
(18) ![]()
Из формулы (18) можно сделать следующие выводы. Если
то схема (15) имеет второй порядок аппроксимации по t и четвертый – по h. Такая схема называется схемой повышенного порядка аппроксимации. Если
![]()
то схема (15) имеет второй порядок аппроксимации по t и по h. При остальных значениях s и при j in є 0 в виде (10), то получим
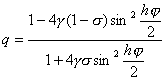
и |q| Ј 1 при всех j , если
![]() (19)
(19)
Отсюда видно, в частности, что все схемы с s і 0,5 абсолютно устойчивы. Схема повышенного порядка аппроксимации (s = s *) также абсолютно устойчива, что проверяется непосредственно.
При s № 0 разностная схема (15) является неявной схемой. Для нахождения решения yin+1 по заданным yin требуется решать систему уравнений
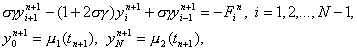 (20)
(20)
![]() где
где
Система (20) решается методом прогонки. Условия устойчивости прогонки при s № 0 сводятся к неравенству
|1 + 2s g | і 2 |s | g
и выполнены при s і – 1/(4g ). Последнее неравенство следует из условия устойчивости (19) разностной схемы.
3.4. Уравнения с переменными коэффициентами и линейные уравнения.Рассмотрим первую краевую задачу для уравнения теплопроводности с переменными коэффициентами
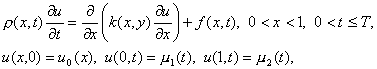 (21)
(21)
где r (x, t), k(x, t), f(x, t) – достаточно гладкие функции, удовлетворяющие условиям
Похожие работы
... пропорциональной второй степени h: Подстановка таких начальных условий в решение сохранит погрешность результатов на уровне . В таком случае говорят, что разностная схема имеет второй порядок точности. 3. Разностные системы уравнений для краевых задач Исходные дифференциальные уравнения во многих физических и технических применениях решаются для случаев, когда заданы значения искомых ...
... схема со сглаживанием, схема прямоугольник со сглаживанием, “шахматная ” схема. Произведены некоторые расчеты для одномерного уравнения переноса с переменными и постоянными коэффициентами на неравномерных сетках, с целью определения наиболее устойчивой разностной схемы. Исследование показало, что наиболее устойчивым методом для одномерного уравнения переноса с переменными коэффициентами является ...
... эксперименты по моделированию распространения таких волн, Крускал и Забуски рассмотрели их столкновение. Остановимся подробнее на обсуждении этого замечательного факта. Пусть имеются две уединенные волны, описываемые уравнением Кортевега—де Фриса, которые различаются амплитудами и движутся друг за другом в одном направлении (рис. 2). Из формулы для уединенных волн (8) следует, что скорость ...
... суммы и позволит вычислить приближенное значение приращения Dy: где Метод четвертого порядка для q = 3, имеет вид где Особо широко известно другое вычислительное правило Рунге-Кутта четвертого порядка точности: где Метод Рунге-Кутта имеет погрешность четвертого порядка (~ h4 ). Правило Рунге. Если приближенный метод имеет порядок погрешности m, то погрешность можно приближенно ...
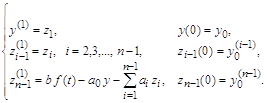
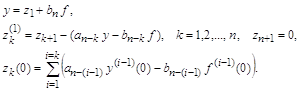
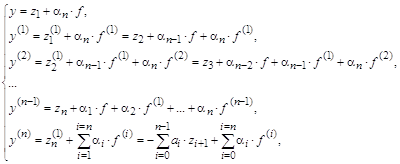
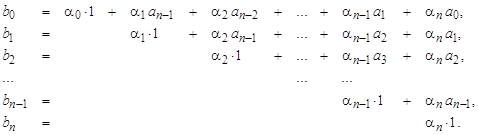



0 комментариев