Выборочные средние отклика (y) для каждого значения x лежат на прямой;

1. Выборочные средние отклика (y) для каждого значения x лежат на прямой;

2. Для любого значения x, соответствующие значения y нормально распределены;

3. Для любого значения x, y – имеют одинаковую дисперсию .

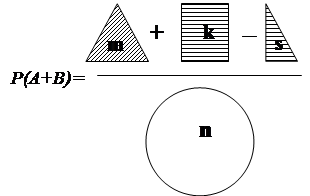
При прогнозировании является ли среднее ошибок оценки подходящей мерой для прогнозирования.

Средняя ошибка оценки всегда равна нулю. Один из способов доказать этот факт, это выбрать в качестве меры прогнозирования дисперсию ошибки оценки.

Стандартная ошибка оценки

Стандартную ошибку оценки применяют для определения пределов, в окрестности предсказанного попадает фактическое значение yi.

В приделах Se – расположено 69% фактических значений объекта, в приделах 2Se – 95%, в приделах 3Se – 97,5%.

Связь b1 и b0 с другими описательными статистиками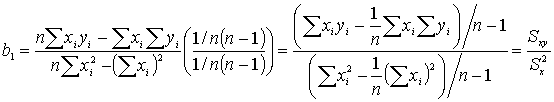

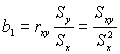
Если x и y распределены по нормальному закону и имеют одинаковую дисперсию, то .

Поскольку rxy не зависит от Sx и Sy, b1 - принимает максимальное значение при rxy =1 и минимальное значение при rxy = -1, следовательно b1 никогда не может быть больше , при rxy =1 и не может быть меньше при rxy = -1.

Если между переменными отсутствует линейная связь, b1=0 уравнение регрессии сводится к прямой без наклона, то есть .

Измерение нелинейной связи между переменными

Для определения меры нелинейной связи между переменными используется коэффициент

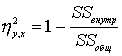
Эта мера может быть использована и для оценки линейной связи.

Пример вычисления:

x/возраст	10	14	18	22	26	30	34	38
	7	8	9	11	9	8	7	8
	8	9	10	11	10	9	9
	9	10	11	12	11	9	10
	9	11	12	12		10
	10

Находим среднее для каждого возраста и суммируем отношения каждого yi от среднего соответствующего группы.

Для 10 - =8,6; 18 – 9,5; 22 – 11,5; 26 – 10; 90 – 9; 34 – 8,67; 38 – 8.

- является мерой нелинейности связи и

Другие меры связи Измерения в дихотомической шкале (например, женат – не женат, мужчина – женщина) Измерение в дихотомической шкале наименований в предположении нормального распределения. Предполагается, что при более полных, более совершенных измерениях данные распределятся по нормальному закону. Шкала порядка Измерение в шкале интервалов или отношений.

Рассмотренный ранее коэффициент кореляции Пирсона соответствует сочетанию J при измерении исходных данных. Для описания степени кореляции при других комбинациях шкал измерений исходных данных используются следующие меры.

Случай A.

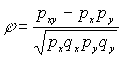
px – доля людей имеющих 1 по x, py – доля людей имеющих 1 по y

qx – доля людей имеющих 0 по x, qy – доля людей имеющих 0 по y

pxy - доля людей имеющих 1 по x и y

№	1	2	3	4	5	6	7	8	9	10	11	12
x	0	1	0	0	1	1	0	1	0	0	0	1
y	0	1	1	0	1	0	0	1	0	1	0	1

x – женат / холост

y – исключенные из учебного заведения / оставшиеся

px =0,4167 ; py = 0,5 ; qx =0,5833 ; qy = 0,5 ; pxy =0,333; φ=0,507

Если нет особого интереса к доле px и py, дихатомические данные располагают в таблице сопряженности признаков. Пример таблицы сопряженности по приведенным данным

φ – Определяется по формуле:

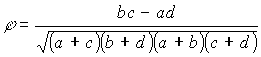
Коэффициент φ, это тот же коэффициент кореляции Пирсона, но эти данные не похожи на двумерное нормальное распределение, которое мы представляли при вычислении коэффициента Пирсона. Это рассматривается как большое неудобство статистиками.

Случай B.

Удовлетворительного коэффициента для этого случая не существует, рекомендуется исходить из предположения о нормальном распределении данных и вычислять φ β качестве меры связи для этого случая.

Случай C.

Для этого случая подходят коэффициенты, о котором мы расскажем в случае I.

Случай D.

Используется биссериальный коэффициент кореляции: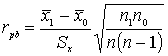

- среднее по x объектов имеющих 1 по y.

- среднее по x объектов имеющих 0 по y.

Sx – стандартное отклонение

Случай E.

Тетрахорический коэффициент кореляции:

Более удобно при расчете обращаться к статическим таблицам, содержащим вычисления из этого уравнения. Они составлены при условии, что bc/ad>1. В противном случае таблица содержит ad/bc и величина тетрахорического коэффициента будет отрицательной.

Случай F.

Удовлетворительного коэффициента не разработано, рекомендуется продположить нормальное распределение для x и использовать биссериальный ранговый коэффициент (см. случай G).

Случай G.

Биссериальный коэффициент: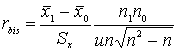

u – ордината нормального распределения.

Случай H.

Используется коэффициент ранговой кореляции Спирмана: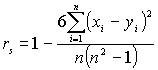

В том случае, если при измерении встречается связанные ранги, это уравнение не подходит в качестве меры кореляции.

Связанный ранг возникает в том случае, если у некоторых объектов получено одинаковое значение переменной. В этом случае ранги, которые должны были бы получить эти объекты суммируются и делятся на количество объектов и каждый получает, пролученный при вычислении ранг.

До сих пор коэффициенты кореляции представляли из себя или могли быть объяснены в терминах произведения моментов. Коэффициент кореляции, не связвнный с моментами построен Кендаллом и называется τ – Кендалла

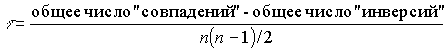
Случай I.

Для этого случая коэффициенты не разработаны, рекомендуется преобразовать оценки по y в ранги и найти или коэффициент Спирмана или Кендалла

Бисериальная ранговая кореляция: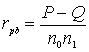

P – сумма всех совпадений; Q – сумма всех инверсий;

n0 – число объектов при нулевой дихотомии; n1– число объектов при единичной дихотомии.