Навигация
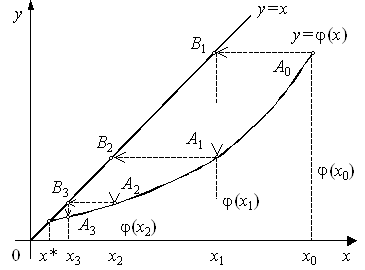
Метод касательных решения нелинейных уравнений
Пензенский приборостроительный колледж
на тему:
Метод касательных решения нелинейных уравнений
Выполнил: Ст-т 22п группы ЛЯПИН Р.Н.
Проверила: ______________
Ковылкино – 1999 г.
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
студент Ляпин Р.Н. группа 22п
Тема: "Метод касательных решения нелинейных уравнений". Изучить теоретический материал по заданной теме. Составить блок схему алгоритма решения задачи . Написать программу на языке Турбо-Паскаль для решения задачи в общем виде. Выполнить программу с конкретными значениями исходных данных. Определить корни уравнения х3 + 0,1 * х2 + 0,4 * х – 1,2 = 0 аналитически и уточнить один из них с точностью до 0,000001 методом касательных Срок представления работы к защите: 10 мая 1999 г. Исходные данные для исследования: научная и техническая литература.
Руководитель курсовой работы: Кривозубова С.А.
Задание принял к исполнению: Ляпин Р.Н.
РЕФЕРАТ
Курсовая работа содержит: страниц, 1 график, 5 источников.
Перечень ключевых понятий: производная, метод касательных, программирование, нелинейное уравнение.
Объект исследования: Корни нелинейного уравнения.
Цель работы: Определение корней нелинейного уравнения.
Методы исследования: изучение работ отечественных и зарубежных авторов по данной теме.
Полученные результаты: изучен метод касательных решения нелинейных уравнений; рассмотрена возможность составления программы на языке программирования Турбо-Паскаль 7.0
Область применения: в работе инженера.
СОДЕРЖАНИЕ
стр.
ВВЕДЕНИЕ........................................ 5
1. Краткое описание сущности метода касательных
( метода секущих Ньютона).................... 7
2. Решение нелинейного уравнения аналитически .. 9
3. Блок схема программы ........................ 11
4. Программа на языке PASCAL 7.0 ............... 12
5. Результаты выполнения программы ............. 13
СПИСОК ИСПОЛЬЗОВАННИХ ИСТОЧНИКОВ ............... 14
ВВЕДЕНИЕ
Процедура подготовки и решения задачи на ЭВМ достаточно сложный и трудоемкий процесс, состоящий из следующих этапов:
Постановка задачи (задача, которую предстоит решать на ЭВМ, формулируется пользователем или получается им в виде задания). Математическая формулировка задачи. Разработка алгоритма решения задачи. Написание программы на языке программирования. Подготовка исходных данных . Ввод программы и исходных данных в ЭВМ. Отладка программы. Тестирование программы. Решение задачи на ЭВМ и обработка результатов.В настоящей курсовой работе условие задачи дано в математической формулировке, поэтому необходимость в выполнении этапов 1 и 2 отпадает и сразу можно приступить к разработке алгоритма решения задачи на ЭВМ. Под алгоритмом понимается последовательность арифметических и логических действий над числовыми значениями переменных, приводящих к вычислению результата решения задачи при изменении исходных данных в достаточно широких пределах. Таким образом, при разработке алгоритма решения задачи математическая формулировка преобразуется в процедуру решения, представляющую собой последовательность арифметических действий и логических связей между ними. При этом алгоритм обладает следующими свойствами: детерминированностью, означающей, что применение алгоритма к одним и тем же исходным данным должно приводить к одному и том уже результату; массовость, позволяющей получать результат при различных исходных данных; результативностью, обеспечивающей получение результата через конечное число шагов.
Наиболее наглядным способом описания алгоритмов является описание его в виде схем. При этом алгоритм представляется последовательность блоков, выполняющих определенные функции, и связей между ними. Внутри блоков указывается информация, характеризующая выполняемые ими функции. Блоки схемы имеют сквозную нумерацию.
Конфигурация и размеры блоков, а также порядок построения схем определяются ГОСТ 19.002-80 и ГОСТ 19.003-80.
На этапе 4 составляется программа на языке Турбо-Паскаль. При описании программы необходимо использовать характерные приемы программирования и учитывать специфику языка. В качестве языка программирования выбран язык ПАСКАЛЬ ввиду его наглядности и облегченного понимания для начинающих программистов, а также возможности в дальнейшем использовать для решения более трудных задач.
Этапы алгоритмизации и программирования являются наиболее трудоемкими, поэтому им уделяется большое внимание.
В процессе выполнения курсовой работы студент готовит исходные данные, вводит программу и исходные данные. При работе ввод программы и исходных данных осуществляется с клавиатуры дисплея.
Отладка программы состоит в обнаружении и исправлении ошибок, допущенных на всех этапах подготовки задач к решению на ПЭВМ. Синтаксис ошибки обнаруживается компилятором, который выдает сообщение, указывающее место и тип ошибки. Обнаружение семантических ошибок осуществляется на этапе тестирования программы, в котором проверяется правильность выполнения программы на упрощенном варианте исходных данных или с помощью контрольных точек или в режиме пошагового исполнения.
Задание при обработке на ЭВМ проходит ряд шагов: компиляцию, редактирование (компоновку) и выполнение.
Обработка результатов решения задачи осуществляется с помощью ЭВМ. Выводимые результаты оформлены в виде, удобном для восприятия.
Похожие работы
... искомого интервала [a, b] являются переменными величинами, которые должны задаваться в каждом конкретном случае с учетом физического смысла решаемой задачи. На втором этапе решения нелинейных уравнений полученные приближенные значения корней уточняются различными итерационными методами до некоторой заданной погрешности. Наиболее эффективные методы уточнения корней уравнения рассмотрены ниже. ...
... для корней уравнения (1). На втором этапе, используя заданное начальное приближение, строится итерационный процесс, позволяющий уточнить значение отыскиваемого корня. Численные методы решения нелинейных уравнений являются, как правило, итерационными методами, которые предполагают задание достаточно близких к искомому решению начальных данных. Существует множество методов решения данной задачи. ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
... (можно предположить единственность корня) Корень отделен на интервале Границы исходного отрезка сдвигаются () Воспользуемся приведенным выше алгоритмом для отделения корня уравнения на заданном отрезке: 1. Разобьем интервал изоляции корня на n отрезков равной длины: 2. Вычисляем значения функции в точках : 3. На концах отрезка (1;2) функция имеет разные ...
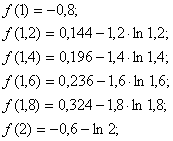

0 комментариев