Навигация
Движение частиц в магнитном поле Земли
24653
знака
10
таблиц
5
изображений
2.2. Движение частиц в магнитном поле Земли
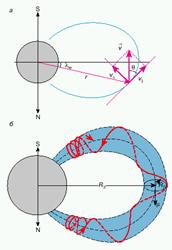
1. Если в магнитном поле скорость заряженной частицы направлена под некотором углом q (так называемый питч-угол) к направлению магнитной силовой линии, где находится частица, то вектор ee скорости можно разложить на две составляющие: по касательной к магнитной силовой линии и перпендикулярно к ней. Движение такой частицы может быть представлено как ларморовское вращение вокруг магнитной силовой линии (центр вращения частицы в магнитном поле называют ведущим центром) и поступательное (движение центра вращения вдоль магнитной силовой линии). В результате сложения этих составляющих частица движется по спиральной траектории, навиваясь на магнитные силовые линии, и, если эти магнитные линии замкнутые, возникает обычный эффект магнитного удержания (рис. 2).
|
|
| Рис. 2. а) - разложение вектора скорости на две составляющие; б) - движение частицы между зеркальными точками. |
Радиус вращения Rл вокруг силовой линии, обычно называемый ларморовским, определяется из равенства центробежной силы и силы Лоренца. Период обращения Tл составляет
|
| (2) |
где m - масса частицы, c - скорость света, Ze - заряд частицы, а 
- составляющая скорости, перпендикулярная к магнитному полю.
Мы полагаем магнитное поле достаточно однородным и стабильным: его изменения в пространстве и во времени очень малы на протяжении ларморовского радиуса и одного периода обращения, из-за чего выполняются условия
|
| (3) |
|
| (4) |
Ограничения (3) и (4) удовлетворяют условиям адиабатичности. При их выполнении задача о движении заряженной частицы в магнитном поле решается просто, а величины Rл и Tл определяются достаточно точно. Например, для электрона и протона с энергией 10 МэВ ларморовские радиусы составляют соответственно 12,2 и 118 км, а периоды их вращения ~10-6 и ~10-3 с. Конечно, ларморовский радиус частиц должен быть гораздо меньше радиуса Земли. Это нужно для выполнения условий адиабатичности (для чего достаточно соотношения Rл/Rз 
0,1). Есть и еще одно ограничение:Rл должен быть достаточно малым, чтобы частица при своем вращении не задевала плотных слоев атмосферы, граница которой находится на высоте ~100 км.
Рассмотрим теперь поступательное движение. Двигаясь по инерции вдоль магнитной силовой линии дипольного поля, частица приближается к Северному или Южному магнитному полюсу, причем напряженность поля сильно увеличивается. На частицу действует сила 
нарастающая по мере приближения к полюсу (Br - радиальная составляющая магнитного поля). Она замедляет поступательное движение частицы к полюсу до полной остановки, после чего заставляет частицу двигаться с ускорением к противоположному полюсу. Точку, где движение частицы вдоль магнитной силовой линии изменяет направление на обратное, называют зеркальной точкой. Для электронов и протонов с энергией 10 МэВ периоды колебаний между парой зеркальных точек РПЗ составляют секунду и десятую долю секунды соответственно.
Помимо этих двух видов движения захваченной частицы существует и третий. В дипольном магнитном поле нельзя полностью выполнить условие адиабатичности (3), особенно для захваченных частиц с высокими энергиями. Действительно, когда частица совершает один оборот вокруг магнитной силовой линии, она пересекает области с разной напряженностью магнитного поля: оно больше на внутренней части ларморовской окружности, чем на внешней. Следовательно, и ларморовский радиус меньше на внутренней части, чем на внешней. По этой причине частица, совершив полный оборот, промахивается мимо исходной точки, так что ведущий центр смещается к западу в случае положительного заряда частицы или к востоку в случае отрицательного. Смещение будет происходить и на последующих витках. Так возникает третий вид движения - долготный дрейф. Частица оборачивается вокруг Земли именно из-за долготного дрейфа: период обращения обратно пропорционален энергии частицы. Для электронов и протонов с энергией ~10 МэВ этот период равен приблизительно двум минутам и нескольким десяткам секунд соответственно.
Похожие работы
... , которые высыпаются на средних широтах. (В данной главе рассмотрены различные случаи высыпаний высокоэнергичных частиц под воздействием различных типов волн: свистов и ионно-циклотронных) Во время геомагнитных возмущений высыпание энергичных электронов из радиационных поясов Земли может быть основным источником притока энергии для ионизации среднеширотной мезосферы. Один особенно интенсивный ...
... - излучение, Геомагнетизм и аэрономия, Т. 18, №2, с. 352-353, 1978. Иванова Т.А., Павлов Н.Н., Рейзман С.Я., Рубинштейн И.А., Сосновец Э.Н., Тверская Л.В., Динамика внешнего радиационного пояса релятивистских электронов в минимуме солнечной активностиб Геомагнетизм и аэрономия, Т. 40, № 1, с. 13-18, 2000. Ильин В.Д., Кузнецов С.Н., Неадиабатические эффекты движения частиц в статическом дипольном ...
... ;s и излучения εs, приводящие к повышению температуры СБ). Потемнение защитных стекол под воздействием ультрафиолетовой части солнечного спектра было впервые обнаружено при полетах искусственных спутников на ГСО. Исследования, проведенные в наземных условиях, показали, что под влиянием УФ-излучения прозрачность этих стекол вначале быстро снижается (примерно на 10%) , оставаясь после этого ...
... около 4.7 млрд. лет тому назад вместе с другими планетами. 1.1 Солнце как звезда Солнце - ближайшая к Земле звезда, является рядовой звездой нашей Галактики. Это карлик главной последовательности диаграммы Герцшпрунга-Рессела. Принадлежит к спектральному классу G2V. Ее физические характеристики: · Масса 1.989 1030 кг · Радиус 696 тыс. км · Температура поверхности 5780 K; · ...
0 комментариев