Навигация
При движении заряженной частицы в дипольном магнитном поле возникают два так называемых адиабатических инварианта движения
24653
знака
10
таблиц
5
изображений
2. При движении заряженной частицы в дипольном магнитном поле возникают два так называемых адиабатических инварианта движения.
Первый инвариант. Ларморовское вращение частицы приводит к сохранению магнитного момента 
, где 
- ток частиц, 
- частота ларморовского вращения и e - заряд частицы. Учитывая (2), получаем выражение
|
| (5) |
Если частицы не подвергаются торможению, а поле стационарно, то 
const. Таким образом, 
и есть первый адиабатический инвариант - сохраняющаяся величина в процессе движения захваченной частицы. В каждый момент времени магнитный момент направлен по касательной к магнитной силовой линии, следуя за всеми ее изгибами. Иными словами, ведущий центр обладает магнитным моментом и движется вдоль магнитной силовой линии. Поскольку 
изменяется вдоль магнитной силовой линии, то соответственно поменяется и питч-угол. При некотором значении напряженности магнитного поля 
станет равным единице. Значит, в соответствующей точке скорость частицы 
перпендикулярна к и дальнейшее продвижение вдоль силовой линии к полюсу прекращается. Это и есть математическое определение зеркальной точки. После остановки в зеркальной точке тотчас же начинается обратное спиральное движение частицы к противоположному полюсу. Из выражения (5) следует, что если на магнитном экваторе частица имела питч-угол определенной величины, то ему соответствует значение поля Bз , при котором произойдет зеркальное отражение. Используя выражения (1) и (2), можно установить, на какой географической широте поле становится равным расчетной величине Bз .
В стационарных условиях осцилляции могли бы продолжаться бесконечно, но захваченные частицы непрерывно растрачивают энергию на ионизацию остаточной атмосферы, синхротронное излучение (электроны) и на рассеяние на электромагнитных волнах. Все это приводит к потере скорости и изменению питч-угла частиц, что сильно влияет на условия их движения. Особенно критичной оказывается высота зеркальных точек. Если она выше условной верхней границы атмосферы, то ионизационные потери пренебрежимо малы и число осцилляций велико. Если при долготном дрейфе зеркальные точки нигде не опускаются ниже 100 км, то частица обойдет Землю без каких-либо последствий. Для частиц с нулевым питч-углом на магнитном экваторе зеркальных точек нет: они проникают в плотные слои атмосферы, достигают поверхности Земли, где погибают.
Второй адиабатический инвариант (долготный). Интеграл действия J при осцилляциях между северной Зс и южной Зю зеркальными точками
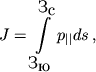
где 
- составляющая импульса вдоль магнитной силовой линии, а ds - элемент пути. Учитывая, что в зеркальной точке sin2
= 1/Bз , находим, что 
В магнитном поле p = const и
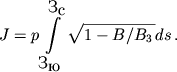
Введем величину
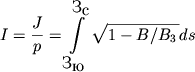
Если за время каждой осцилляции частицы между двумя зеркальными точками значение I сохраняется и частица совершает при этом долготный дрейф, то можно считать, что она все время находится на вполне определенных силовых линиях. Совокупность этих силовых линий составляет поверхность (рис. 3) и называется оболочкой. Оболочка напоминает замкнутый выпуклый пояс, где верхний и нижний края - это множество широт расположения зеркальных точек. Края пояса, его выпуклость или вогнутость зависят уже от реальной конфигурации дипольного магнитного поля Земли. Пояс для конкретной частицы имеет толщину, определяемую ее ларморовским радиусом. Захваченные частицы отличаются импульсами, питч-углами и т.п. и каждая имеет свой пояс. Все вместе они образуют РПЗ.
|
|
| Рис. 3. Меридиональное сечение радиационного пояса Земли. Оболочки L = 1-3 - внутренняя часть пояса; L = 3,5-7 - внешняя часть; L = 1,2-1,5 - стабильный пояс высокоэнергетичных электронов (см. раздел 3.1); L ~ 2 - стабильный пояс ядер аномальной компоненты космических лучей (см. раздел 3.2); L ~ 2,6 - квазистабильный пояс (см. раздел 3.3). |
Похожие работы
... , которые высыпаются на средних широтах. (В данной главе рассмотрены различные случаи высыпаний высокоэнергичных частиц под воздействием различных типов волн: свистов и ионно-циклотронных) Во время геомагнитных возмущений высыпание энергичных электронов из радиационных поясов Земли может быть основным источником притока энергии для ионизации среднеширотной мезосферы. Один особенно интенсивный ...
... - излучение, Геомагнетизм и аэрономия, Т. 18, №2, с. 352-353, 1978. Иванова Т.А., Павлов Н.Н., Рейзман С.Я., Рубинштейн И.А., Сосновец Э.Н., Тверская Л.В., Динамика внешнего радиационного пояса релятивистских электронов в минимуме солнечной активностиб Геомагнетизм и аэрономия, Т. 40, № 1, с. 13-18, 2000. Ильин В.Д., Кузнецов С.Н., Неадиабатические эффекты движения частиц в статическом дипольном ...
... ;s и излучения εs, приводящие к повышению температуры СБ). Потемнение защитных стекол под воздействием ультрафиолетовой части солнечного спектра было впервые обнаружено при полетах искусственных спутников на ГСО. Исследования, проведенные в наземных условиях, показали, что под влиянием УФ-излучения прозрачность этих стекол вначале быстро снижается (примерно на 10%) , оставаясь после этого ...
... около 4.7 млрд. лет тому назад вместе с другими планетами. 1.1 Солнце как звезда Солнце - ближайшая к Земле звезда, является рядовой звездой нашей Галактики. Это карлик главной последовательности диаграммы Герцшпрунга-Рессела. Принадлежит к спектральному классу G2V. Ее физические характеристики: · Масса 1.989 1030 кг · Радиус 696 тыс. км · Температура поверхности 5780 K; · ...
0 комментариев