Навигация
2.2. Формула Даламбера.
Изучение методов построения решений краевых задач для уравнений гиперболического типа начнем с задачи с начальными условиями для неограниченной струны:
(2)
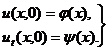(3)
Преобразуем это уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик
распадается на два уравнения:
, 
,
интегралами которых являются прямые
, 
.
Вводя новые переменные
, 
,
уравнение колебания струны преобразуем к виду:
. (4)
Найдем общий интеграл последнего уравнения. Очевидно, для всякого решения уравнения (4)
,
где 
- некоторая функция только переменного 
. Интегрируя это равенство по при фиксированном 
, получим
, (5)
где 
и 
являются функциями только переменных и .Обратно, каковы бы ни были дважды дифференцируемые функции и , функция 
, определяемая формулой (5), представляет собой решение уравнения (4). Так как всякое решение уравнения (4)может быть представлено в виде (5) при соответствующем выборе и , то формула (5) является общим интегралом этого уравнения. Следовательно, функция
(6)
является общим интегралом уравнения (2).
Допустим, что решение рассматриваемой задачи существует; тогда оно дается формулой (6). Определим функции и таким образом, чтобы удовлетворялись начальные условия:
(7)
. (8)
Интегрируя второе равенство, получим:
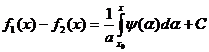
где 
и C – постоянные. Из равенства
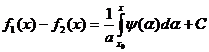
находим:
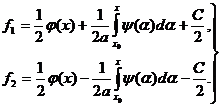(9)
Таким образом, мы определили функции и через заданные функции 
и 
, причем равенства (9) должны иметь место для любого значения аргумента. Подставляя в (6) найденные значения и , получим:
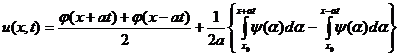
или
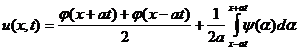, (10)
Формулу (10), называемую формулой Даламбера, мы получили, предполагая существование решения поставленной задачи. Эта формула доказывает единственность решения. В самом деле, если бы существовало второе решение задачи (2) – (3), то оно представлялось бы формулой (10) и совпадало бы с первым решением.
Нетрудно проверить, что формула (10) удовлетворяет (в предположении двукратной дифференцируемости функции и однократной дифференцируемости функции ) уравнению и начальным условиям. Таким образом, изложенный метод доказывает как единственность, так и существование решения поставленной задачи.
2.2.2.Физический интерпретация.
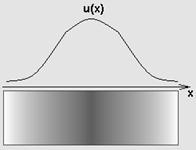
Функция 
, определяемая формулой (10), представляет собой процесс распространения начального отклонения и начальной скорости. Если фиксировать 
, то функция 
дает профиль струны в момент 
, фиксируя 
, получим функцию 
, дающую процесс движения точки . Предположим, что наблюдатель, находившийся в точке x=0 в момент t=0, движется со скоростью a в положительном направлении. Введем систему координат, связанную с наблюдателем, полагая 
, 
. В этой подвижной системе координат функция 
будет определятся формулой 
и наблюдатель все время будет видеть тот же профиль, что и в начальный момент. Следовательно, функция представляет неизменный профиль f(x), перемещающийся вправо (в положительном направлении оси x) со скоростью a (распространяющуюся или бегущую волну). Функция f(x+at) представляет, очевидно, волну, распространяющуюся налево (в отрицательном направлении оси x) со скоростью a. Таким образом, общее решение (10) задачи Коши для бесконечной струны есть суперпозиция двух волн 
, одна из которых распространяется направо со скоростью a, а вторая – налево с той же скоростью. При этом
,
где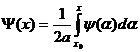 
.
Для выяснения характера решения (10) удобно пользоваться плоскостью состояний (x,t) или «фазовой плоскостью». Прямые x-at=const и x+at=const являются характеристиками уравнения (2). Функция 
вдоль характеристики x-at=const сохраняет постоянное значение, функция 
постоянна вдоль характеристики x+at=const.
Предположим, что f(x) отлична от нуля только в интервале 
и равна нулю вне этого интервала. Проведем характеристики 
и 
через точки 
и 
; они разбивают полуплоскость (x,t>0) на три области I, II, и III (рис. 3, а).
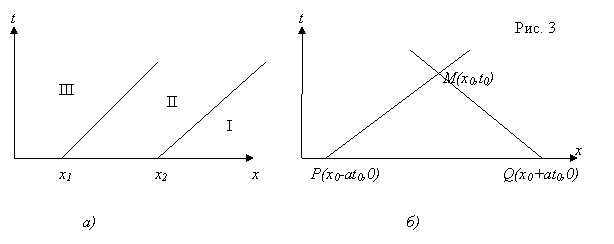
Функция отлична от нуля только в области II, где 
и характеристики и представляют передний и задний фронты распространяющейся направо волны.
Рассмотрим теперь некоторую фиксированную точку 
и приведем из нее обе характеристики 
и 
, которые пересекут ось x в точках 
, t=0 и 
, t=0. Значение функции 
в точке равно 
, т. е. определяется значениями функций 
и 
в точках и , являющихся вершинами треугольника MPQ (рис. 3, б), образованного двумя характеристиками и осью x. Этот треугольник называется характеристическим треугольником точки . Из формулы (10) видно, что отклонение 
точки струны в момент зависит только от значений начального отклонения в вершинах P(x0-at0,0) и Q(x0+at0,0) характеристического треугольника MPQ и от значений начальной скорости на стороне PQ. Это становится особенно ясным, если формулу (10) записать в виде
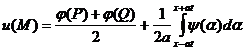(11)
Начальные данные, заданные вне PQ, не оказывают влияния на значения в точке 
. Если начальные условия заданы не на всей бесконечной прямой, а на отрезке 
, то они однозначно определяют решение внутри характеристического треугольника, основанием которого является отрезок .
Похожие работы
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...
... менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные ...
... Дис-петчер 1.1 3 Рис. 5. HIPO-диаграмма. Задание к лабораторной работе С помощью HIPO-технологии составить внешние спецификации для комплекса программ решения одной из следующих задач. 1.Численное решение задачи Коши для дифференциального уравнения методом Рунге-Кутта и Адамса с автоматическим выбором шага и заданным шагом. 2.Интерполирование табличной функции. 3.Численное ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
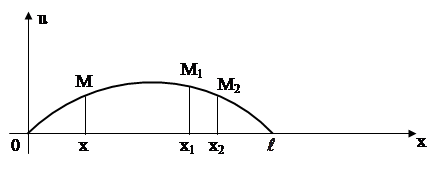
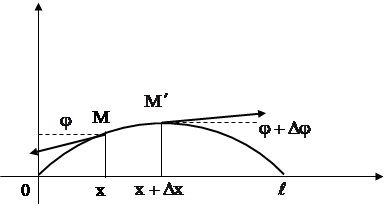
0 комментариев