Навигация
2.2.3. Пример.
Решение (10) можно представить в виде суммы ![]() , где
, где
![]() (12)
(12)
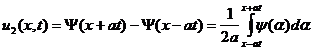 . (13)
. (13)
Если начальная скорость равна нулю (![]() ), то отклонение
), то отклонение ![]() есть сумма левой и правой бегущих волн, причем начальная форма обеих волн определяется функцией
есть сумма левой и правой бегущих волн, причем начальная форма обеих волн определяется функцией ![]() , равной половине начального отклонения. Если же
, равной половине начального отклонения. Если же ![]() , то
, то ![]() представляет возмущение струны, создаваемое начальной скоростью.
представляет возмущение струны, создаваемое начальной скоростью.
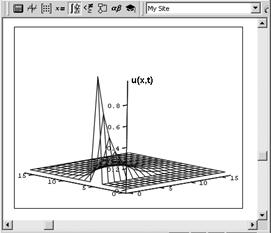
Рассмотрим распространение начального отклонения, заданного в виде равнобедренного треугольника. Такой начальный профиль можно получить, если оттянуть струну в середине отрезка ![]() . На рис. 4 даны последовательные положения струны через промежутки времени
. На рис. 4 даны последовательные положения струны через промежутки времени ![]() .
.
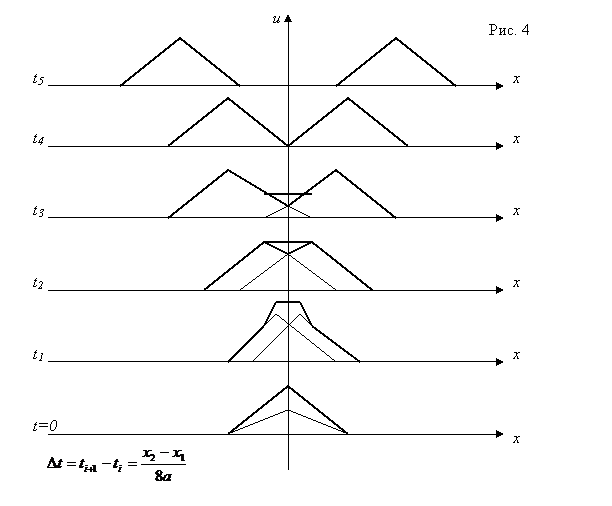
Наглядное представление о характере процесса распространения можно получить с помощью фазовой плоскости (x, t). Проведем характеристики через точки ![]() и
и ![]() ; они разобьют полуплоскость
; они разобьют полуплоскость ![]() на шесть областей (рис. 5).
на шесть областей (рис. 5).
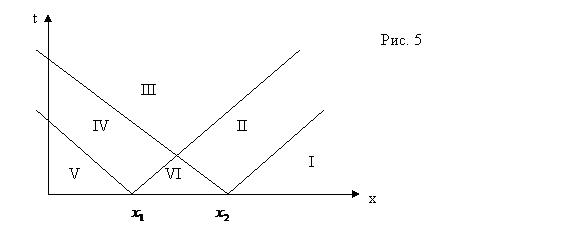
Отклонение ![]() в любой точке (x,t) дается формулой (12). Поэтому в областях I, III, V отклонение равно нулю, так как характеристический треугольник любой точки из этих областей не имеет общих точек с отрезком
в любой точке (x,t) дается формулой (12). Поэтому в областях I, III, V отклонение равно нулю, так как характеристический треугольник любой точки из этих областей не имеет общих точек с отрезком ![]() , на котором заданы начальные условия. В области II решением является «правая волна»
, на котором заданы начальные условия. В области II решением является «правая волна» ![]() , в области IV – «левая волна»
, в области IV – «левая волна» ![]() , а в области VI решение есть сумма «левой» и «правой» волн.
, а в области VI решение есть сумма «левой» и «правой» волн.
3. О колебании стержней.
В курсах методов математической физики основное место отводится уравнениям второго порядка. Однако большое число задач о колебаниях стержней, пластин и т.д. приводит к уравнениям более высокого порядка.
В качестве примера на уравнения 4-го порядка рассмотрим задачу о собственных колебаниях камертона, эквивалентную задаче о колебаниях тонкого прямоугольного стержня, зажатого одним концом в массивные тиски. Определение формы колебаний камертона и его частоты сводится к решению «уравнения поперечных колебаний стержня»
![]() (1)
(1)
К этому уравнению приходят во многих задачах о колебании стержней, при расчете устойчивости вращающихся валов, а также при изучении вибрации кораблей.
Приведем элементарный вывод уравнения (1). Рассмотрим прямоуголный стержень длиной ![]() , высотой h и шириной b. Выделим элемент длины dx. После изгиба торцевые сечения выделенного элемента стержня, предполагаемые плоскими, образуют угол
, высотой h и шириной b. Выделим элемент длины dx. После изгиба торцевые сечения выделенного элемента стержня, предполагаемые плоскими, образуют угол ![]() , Если деформации малы, а длина оси стержня при изгибе не меняется (dl=dx), то
, Если деформации малы, а длина оси стержня при изгибе не меняется (dl=dx), то
![]() .
.
Слой материала, отстоящий от оси стержня y=0 на расстоянии ![]() , изменяет свою длину на величину
, изменяет свою длину на величину ![]() . По закону Гука сила натяжения, действующая вдоль слоя, равна
. По закону Гука сила натяжения, действующая вдоль слоя, равна
![]() ,
,
где E – модуль упругости материала стержня. Полный изгибающий момент сил, действующих на сечение x, равен
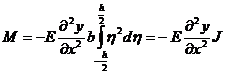 , (2)
, (2)
где
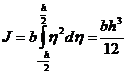
- момент инерции прямоугольного сечения относительно своей горизонтальной оси. Обозначим через M(x) момент, действующих на правую часть стержня в каждом сечении. В сечении x+dx, очевидно, действует момент сил, равный –(M+dM).
Избыточный момент –dM уравновешивается моментом тангенциальных сил
![]() .
.
Отсюда в силу равенства (2) получаем величину тангенциальной силы
![]() . (3)
. (3)
Приравняв действующую на элемент результирующую силу
![]()
произведению массы элемента на ускорение
![]() ,
,
где ![]() - плотность стержня, S – площадь поперечного сечения (при этом мы пренебрегаем вращательным движением при изгибе), получаем уравнение поперечных колебаний стержня
- плотность стержня, S – площадь поперечного сечения (при этом мы пренебрегаем вращательным движением при изгибе), получаем уравнение поперечных колебаний стержня
![]() (
(![]() ). (1)
). (1)
Граничными условиями для заделанного конца x=0 являются неподвижность стержня и горизонтальность касательной
![]() ,
, ![]() . (4)
. (4)
На свободном конце должны равняться нулю изгибающий момент (2) и тангенциальная сила (3), откуда следует, что
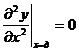 ,
, 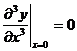 . (5)
. (5)
Для того чтобы полностью определить движения стержня, нужно еще задать начальные условия – начальное отклонение и начальную скорость
![]() ,
, ![]() (
(![]() ). (6)
). (6)
Таким образом, задача сводится к решению уравнения (1) с граничными условиями (4), (5) и с начальными условиями (6).
Будем решать задачу методом разделения переменных, полагая
y=Y(x)T(t). (7)
Подставляя предлагаемую форму решения в (1), имеем:
![]() .
.
Для функции Y(x) получаем задачу о собственных значениях
![]() , (8)
, (8)
![]() ,
, ![]() ,
, 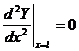 ,
, 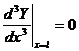 . (9)
. (9)
Общее решение уравнения (8) представляется в виде
![]() .
.
Из условий Y(0)=0, Y’(0)=0 находим C=-A, D=-B. Отсюда следует, что
![]() .
.
Условия Y’’(l)=0 и Y’’’(l)=0 дают:
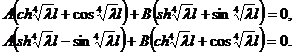
Эта однородная система имеет нетривиальные решения A и B, если определитель системы равен нулю. Приравнивая этот определитель нулю, получаем трансцендентное уравнение для вычисления собственных значений
![]() .
.
Так как ![]() , то это уравнение можно записать в идее
, то это уравнение можно записать в идее
![]() (
(![]() ). (10)
). (10)
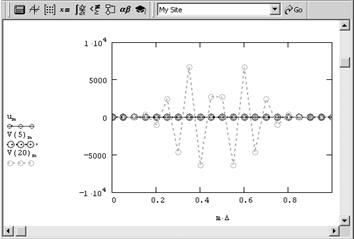
Корни уравнения (10) без труда вычисляются, например, графически
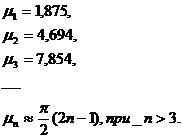
Последняя формула дает значение ![]() с точностью до трех десятичных знаков, начиная с n=3, и с точностью до шестого знака для
с точностью до трех десятичных знаков, начиная с n=3, и с точностью до шестого знака для ![]() .
.
Рассмотрим теперь частоты колебаний камертона. Уравнению
![]()
Удовлетворяют тригонометрические функции
![]()
с частотой
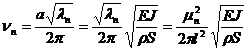 ,
,
Частоты ![]() собственных колебаний относятся как квадраты
собственных колебаний относятся как квадраты ![]() . Так как
. Так как
![]() ,
,
То второй собственный тон выше основного тона более чем на две с половиной октавы, т.е. выше шестой гармоники струны при равном основном тоне, третье же собственное колебание выше основного тона более чем на четыре октавы. Например, если камертон имеет основную частоту в 440 колебаний в секунду (принятый стандарт a’ – ноты ля первой октавы), то следующая собственная частота камертона будет 2757,5 колебания в секунду (между c’’’’ =2637,3 и f’’’’=2794,0 – между нотами ми и фа четвертой октавы равномерно-темперированной гаммы), третья же собственная частота в 7721,1 колебания в секунду уже выходит за пределы шкалы собственно музыкальных звуков.
При возбуждении колебаний камертона ударом присутствует не только первая, но и высшие гармоники, чем и объясняется металлический звук в начальный момент. Однако с течением времени высшие гармоники быстро затухают и камертон издает чистый звук основного тона.
4. Заключение.Дифференциальные уравнения с частными производными широко применяются в математической физике. В качестве примера в данной работе рассмотрены два уравнения.
Волновое уравнение с краевыми условиями можно свести к решению формулы Даламбера, задающуюся начальными условиями. И с помощью фазовой плоскости можно отследить характер его решения.
В процессе решения «уравнения поперечных колебаний стержня» получаем задачу о собственных значениях и задачу о нахождение частот собственных колебаний. Причем частоты собственных колебаний относятся как квадраты собственных значений.
Список литературыА. Н. Тихонов, А. А. Самарский «Уравнения математической физики», Москва, 1966 г.
Н. С. Пискунов «Дифференциальное и интегральное исчисление», Москва, 1970 г.
Н. С. Кошляков, Э. Б. Глинер, М. М. Смирнов «Уравнения в честных производных математической физики», Москва, 1970
Похожие работы
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...
... менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные ...
... Дис-петчер 1.1 3 Рис. 5. HIPO-диаграмма. Задание к лабораторной работе С помощью HIPO-технологии составить внешние спецификации для комплекса программ решения одной из следующих задач. 1.Численное решение задачи Коши для дифференциального уравнения методом Рунге-Кутта и Адамса с автоматическим выбором шага и заданным шагом. 2.Интерполирование табличной функции. 3.Численное ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
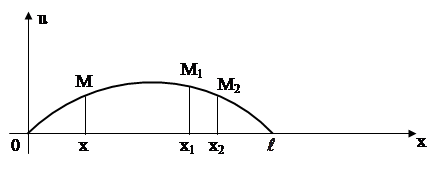
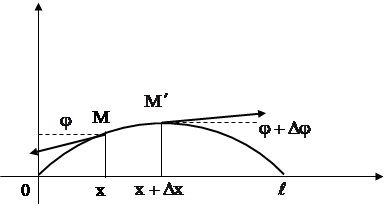
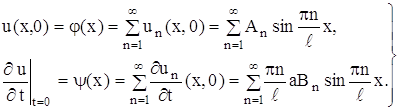
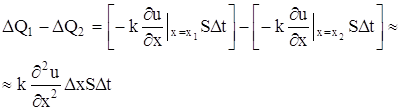
0 комментариев