Навигация
Некоторые приложения определенного интеграла в математике
7939
знаков
0
таблиц
1
изображение
Курсовая работа студента гр. МТ-21
Нургалиев А.З.
Павлодарский университет
Павлодар 2005 год.
1. Введение.В курсовой работе рассмотрены вопросы некоторого приложения определенного интеграла. Цель: изучить актуальность применения определенного интеграла и широту его использования в математике, оценить ее практическую и теоретическую значимость.
При разработки данного вопроса, был также рассмотрен несобственный интеграл, как частный случай определенного интеграла, его определение и виды.
2. Определенный интеграл.
Пусть функция f(x) задана в некотором промежутке [a,b]. Разобьем этот промежуток произвольным образом на части, вставив между a и b точки деления: 
. Наибольшую из разностей
(i=0,1,2, …,n-1) будем впредь обозначать через λ.
Возьмем в каждом из частных промежутков 
по произволу точку 
и составим сумму
.
Говорят, что сумма σ при λ→0 имеет (конечный) предел I, если для каждого числа ε>0 найдется такое число δ>0, что, лишь только λ<δ (т.е. основной промежуток разбит на части, с длинами 
), неравенство
выполняется при любом выборе чисел 
.
Записывают это так:
. (1)
Этому определению «на языке ε-δ», как обычно, противопоставляется определение «на языке последовательностей». Представим себе, что промежуток [α,b] последовательно разбивается на части, сначала одним способом, затем – вторым, третьим и т.д. Такую последовательность разбиений промежутка на части мы будем называть основной, если соответствующая последовательность значений 
сходится к нулю.
Равенство (1) можно понимать теперь и в том смысле, что последовательность значений суммы σ, отвечающая любой основной последовательности разбиений промежутка, всегда стремится к пределу I, как бы ни выбирать при этом .
Второе определение позволяет перенести основные понятия и предложения теории пределов и на этот новый предел.
Конечный предел I суммы σ при λ→0 называется определенным интегралом функции f(x) в промежутке от α до b и обозначается символом
;
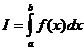в случае существования такого предела функции f(x) называется интегрируемой в промежутке [α,b].
Числа α и b носят название, соответственно, нижнего и верхнего пределов интеграла. При постоянных пределах определенный интеграл представляет собой постоянное число.
3. Несобственные интегралы.
Пусть f непрерывна на луче на луче 
и F(x) – первообразная для f на луче . Если существует
,
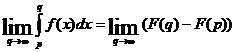то этот предел обозначается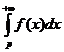 
и называется сходящимся несобственным интегралом.
Несобственные интеграл вида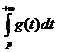 
и аналогичный интеграл
получаются при замене в интеграле Римана с помощью функции t=t(x), непрерывной и дифференцируемой на полуинтервале [a,b) ( или (a,b] ) и являющейся бесконечно большой определенного знака при 
(или 
).
Здесь существенно, что особой точкой функции t является именно конец (левый или правый) отрезка [a,b]. Если особой точкой t(x) (как в разобранном выше примере) является внутренняя точка с интервала (a,b), то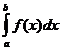 
разбивается на 
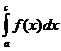и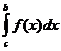 
, и переход к аргументу t делается раздельно в каждом из слагаемых.
Пример.
Вычислим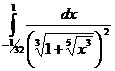 
.
Пусть 
,
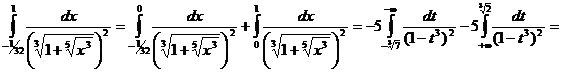
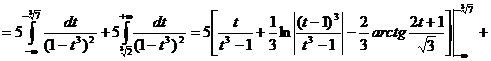
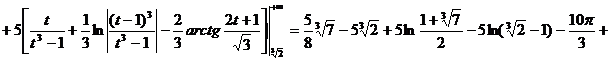
Другим видом несобственного интеграла является интеграл 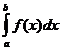, если функция f не ограничена на 
, но непрерывна на 
при любом 
, 
(или на 
), т.е. не ограничена в окрестности точки 
(точки b).
Этот интеграл существует (сходится), если существует:
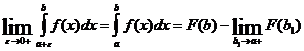
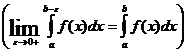
Пример.
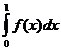, если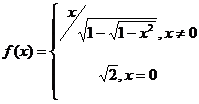 
f(x) непрерывна на [0,1]. После замены 
получаем
.
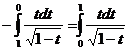не ограничена на [0,1], т.к. первообразная функция на 
при любом , 
равна: 
, то
.
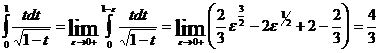Несобственный интеграл может появится и при интегрировании по частям.
,
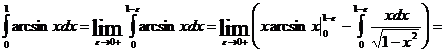
т.е.
,
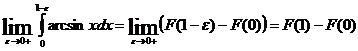где 
- первообразная для arcsinx на [0,1].
4.1.Формула Валлиса.
Для вывода формулы Валлиса необходимо вычислить следующий интеграл:
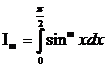(при натуральном m).
Интегрируя по частям, найдём
.
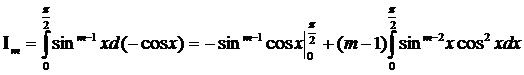Двойная подстановка обращает в нуль. Заменяя 
через 
, получим
откуда рекуррентная формула:
,
по которой интеграл 
последовательно приводится к 
и 
. Именно, при m=2n имеем
,
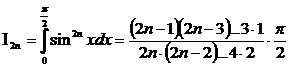если же m=2n+1, то
.
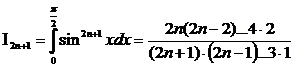Такие же точно результаты получаются и для .
Для более короткой записи найденных выражений воспользуемся символом m!!(произведение натуральных чисел, не превосходящих m и одной с ним чётности). Тогда можно будет написать
 |
|
|
при m не
четном нечётном.
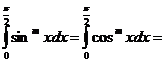(1) Из формулы (1) можно вывести знаменитую формулу Валлиса (J. Wallis).
Предполагая 0<x<
, имеем неравенства
.
Проинтегрируем эти неравенства в промежутке от 0 до :
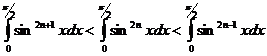
Отсюда, в силу (1), находим
или
.
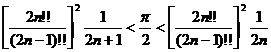Так как разность между двумя крайними выражениями
,
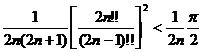очевидно, стремится к 0 при 
, то 
является их общим пределом. Итак,
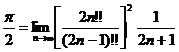
или
.
Отсюда в свою очередь вытекает
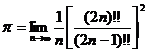
Эта формула носит название формулы Валлиса. Она дает довольно простое выражение числа p через натуральные числа. Теоретически этот результат интересен. Что касается ценности этой формулы как средства фактического вычисления p, то она невелика. Именно, чтобы получить удовлетворительную точность, надо взять n довольно большим, а тогда выражение 
оказывается весьма громоздким.
Похожие работы
... десятичной дробью, такие как π , , и т.д. 5) комплексные числа, вводящие в рассмотрение «мнимое число» . История развития числа от целого числа до иррационального знакома нам по школьному курсу. С эпохи Возрождения математики стали использовать числа вида z = x+iy для решения квадратных уравнений, дискриминант у которых отрицателен, где i =, i² = –1, х и у – вещественные числа Само ...
бнику, решения задач необходимо ответить на вопросы для самопроверки, помещенные в конце темы. В соответствии с действующим учебным планом студенты-заочники изучают курс высшей математики в течение 1 и 2 семестра и выполняют в каждом семестре по две контрольные работы. Первая и вторая контрольные работы выполняются студентами в 1 семестре после изучения тем 1-2 и 3-4 соответственно. Третья и ...
... ( процедура TABL ) и интеграл. 4. Заключение и выводы. Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное. Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же ...
... for i: = n-1 to n do; c[i]: = 1 - c[n+1-i]; end; {заполнение y-ков в массиве у[5]} procedure form(var x:aa; var y:aa); var i:integer; Begin for i:=1 to n do y[i]:=sin(x[i]); {функция} end; {процедура для расчета интеграла по квадратурной формуле Чебышева} procedure cheb(var y:aa;var ich:real); var i:integer; Begin ich: = 0; for i: = 1 to n do ich: = ich+y[i]*h; end; {процедура вывода таблицы} ...
0 комментариев