Навигация
Применение формулы Валлиса для интеграла Эйлера-Пуассона
7939
знаков
0
таблиц
1
изображение
4.2. Применение формулы Валлиса для интеграла Эйлера-Пуассона.
Интеграл Эйлера-Пуассона имеет вид:
;
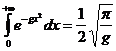Приведём метод его нахождения. Мы знаем что положив:
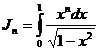(т.к.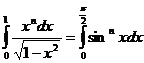 
),
имеем соотношение:
;
отсюда заключаем:
,
что дает:
.
Установив это, замечаем, что предел отношения 
при бесконечно большом n равен единице; действительно, так как 
убывает при возрастании n, то мы имеем неравенство:
или:
.
Мы видим, следовательно, что заключается между единицей и дробью 
, которая также равна единице при бесконечном n.
Установив это, получаем равенство:
,
которое нам дает, если заставим n бесконечно возрастать:
,
и, следовательно:
.
Полагая теперь 
в интеграле 
, мы получим следующее новое выражение:
;
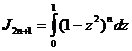заменив затем z на 
, получаем:
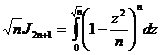
и, следовательно, при бесконечном n
.
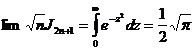Достаточно затем положить 
, чтобы установить результат, к которому мы стремились:
.
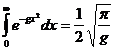4.3. Вывод формулы Тейлора с остаточным членом в интегральной форме.
Формула интегрирования по частям: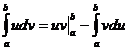 
,
а обобщенная формула примет вид:
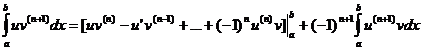. (1)
Положим, что в формуле (1)
. Тогда 
, 
, …, 
, 
; при x=b все функции v, v’, …, 
обращаются в нуль. Пользуясь для u, u’, u’’, … функциональным обозначением f(x), f’(x), f’’(x), …, перепишем (1) в виде
.
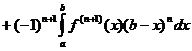Отсюда получается формула Тейлора с дополнительным членом в виде определенного интеграла
.
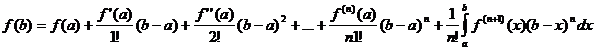Заменим здесь b через x, а 
через 
:
.
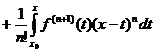Новое выражение для дополнительного члена, не содержит никаких неизвестных чисел.
Если угодно, из этого выражения можно было бы вывести и уже знакомые нам формы дополнительного члена. Например, воспользовавшись тем, что множитель 
подинтегральной функции не меняет знака, можно применить к последнему интегралу обобщенную теорему о среднем
,
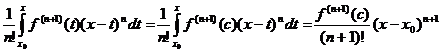где с содержится в промежутке 
. Таким образом, мы вновь получили лангранжеву форму дополнительного члена.
5. Заключение.
В курсовой работе даны определения определенного и несобственного интеграла и его виды, рассмотрены вопросы некоторого приложения определенного интеграла. В частности, формула Валлиса, имеющая историческое значение, как первое представление числа p в виде предела легко вычисляемой рациональной варианты, а также вычисление интеграла Эйлера-Пуассона с помощью этой формулы. Рассмотрен способ получения формулы Тейлора с дополнительным членом в интегральной форме.
Формулой Валлиса в теоретических исследованиях пользуются и сейчас (например, при выведении формулы Стирлинга). Что касается фактического приближенного вычисления p, то существуют методы, гораздо более быстро ведущие к цели.
Интеграл Эйлера-Пуассона применяется при вычислении более сложных несобственных интегралов, встречается в теории вероятности.
Новое выражение для дополнительного члена в формуле Тейлора интересно тем, что оно не содержит никаких неизвестных чисел.
Данную курсовую работу можно использовать в качестве лекционного и справочного материала.
Список литературыФихтенгольц Г. М. «Курс дифференциального и интегрального исчисления»(II том) – Москва, 1970г.
Пискунов Н.С. «Дифференциальное и интегральное исчисления»(I том) - Москва, 1970г.
Эрмит Ш. «Курс анализа» - Москва, 19
Похожие работы
... десятичной дробью, такие как π , , и т.д. 5) комплексные числа, вводящие в рассмотрение «мнимое число» . История развития числа от целого числа до иррационального знакома нам по школьному курсу. С эпохи Возрождения математики стали использовать числа вида z = x+iy для решения квадратных уравнений, дискриминант у которых отрицателен, где i =, i² = –1, х и у – вещественные числа Само ...
бнику, решения задач необходимо ответить на вопросы для самопроверки, помещенные в конце темы. В соответствии с действующим учебным планом студенты-заочники изучают курс высшей математики в течение 1 и 2 семестра и выполняют в каждом семестре по две контрольные работы. Первая и вторая контрольные работы выполняются студентами в 1 семестре после изучения тем 1-2 и 3-4 соответственно. Третья и ...
... ( процедура TABL ) и интеграл. 4. Заключение и выводы. Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное. Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же ...
... for i: = n-1 to n do; c[i]: = 1 - c[n+1-i]; end; {заполнение y-ков в массиве у[5]} procedure form(var x:aa; var y:aa); var i:integer; Begin for i:=1 to n do y[i]:=sin(x[i]); {функция} end; {процедура для расчета интеграла по квадратурной формуле Чебышева} procedure cheb(var y:aa;var ich:real); var i:integer; Begin ich: = 0; for i: = 1 to n do ich: = ich+y[i]*h; end; {процедура вывода таблицы} ...
0 комментариев