Навигация
Педагогические условия интеллектуального развития старшего дошкольника в процессе формирования первичных математических представлений
1.4. Педагогические условия интеллектуального развития старшего дошкольника в процессе формирования первичных математических представлений
Академик А.В.Запорожец писал, что оптимальные педагогические условия для реализации потенциальных возможностей маленького ребенка, для его гармоничного развития создаются не путем форсированного, сверхраннего обучения, направленного на сокращение детства, на преждевременное превращения дошкольника в школьника, а, наоборот, путем широкого развертывания и максимального обогащения специфики детских форм игровой, практической и изобразительной деятельности, а также общение детей друг с другом и со взрослым.
Формирование у детей интеллектуального развития во многом определяет развитие их чувств и поведение. В старший дошкольный период развития учение включено в другие виды деятельности – ребенок общается со взрослым – и учится, он манипулирует предметами – и учится, он играет – и учится.
Наиболее важное значение для развития личности будущего школьника имеет игра. Однако ее ведущая роль определяется не тем, сколько времени отводится ей как деятельности, а тем неоценимым значением, которое она имеет для психического развития, поскольку именно в игре происходят важнейшие изменения в психике ребенка, закладывается основа его отношений с окружающим миром, осуществляется подготовка к переходу малыша на новый этап, к более сложной ведущей деятельности – учению.
Развитие элементарных математических представлений у дошкольников – особая область познания, в которой при условии последовательного обучения можно целенаправленно формировать зрительную память, мыслительный процесс, абстрактное логическое мышление, повышать интеллектуальный уровень.
Необходимыми педагогическими условиями интеллектуального развития старшего дошкольного возраста в процессе формирования первичных математических представлений являются:
наличие четко обоснованных целей и содержания образовательного процесса в дошкольных образовательных учреждениях, направленных на интеллектуальное развитие дошкольников в процессе формирования первичных математических представлений;
учет особенностей детей старшего дошкольного возраста в процессе формирования математических представлений;
использование наглядности, алгоритма;
систематичность работы путем активизации игр и игровых приемов, вызывающих интерес детей к занятиям;
вариативность применения программ дошкольных образовательных учреждений, стимулирующих интеллектуальное развитие дошкольников;
гуманизация образовательного процесса как условие интеллектуального развития дошкольников;
Успешная реализация задач интеллектуального развития дошкольников в процессе формирования математических представлений станет возможной, если обеспечить взаимосвязь психологического, технологического и коммуникативного компонентов в целостном педагогическом процессе.
Психологический компонент - предполагает создание следующих условий:
наполнение жизни ребенка радостью познания, создание эмоционального фона, психологического комфорта и стимулирование детей к творческому поиску;
осуществление мотивации познавательной деятельности ребенка на основе его интересов и стремления познать больше;
создание условия для самореализации, самовыражения и самоутверждения каждой личности ребенка;
учет возрастных особенностей ребенка;
осуществление личностно-деятельностного подхода в образовательном процессе;
внимание к внутреннему миру ребенка, знание индивидуальных особенностей и признание его самоценности, предоставление ему возможности почувствовать себя равным в общении со взрослыми и детьми.
Продуктивной будет работа взрослых с детьми, как показало наше исследование, если она проходит в «общем психологическом пространстве», которое следует рассматривать как непременное условие развития у детей эмоций, уверенности в своих силах, сообразительности.
Формирование математических представлений в дошкольных учреждениях обусловливает необходимость применения новых форм развивающих занятий, обеспечивающих совместное решение с детьми задач, свободный выбор ими занятий, предоставление ребенку свободы действий - работать стоя, сидеть не только за столом, но и на ковре и т.д. Совершенствование педагогической технологии мы связываем с организацией воспитателем такой деятельности, в которую органично вписываются дидактические задачи и развивающее взаимодействие детей, с оставлением на каждом занятии педагогического пространства, чтобы дети подумали о чем-то хорошем, послушали музыку, занялись любимым делом.
Общение - один из источников развития познавательной деятельности. Процесс общения предполагает взаимодействие рационального, эмоционального, волевого и практического компонентов, утверждение объектно-субъектной основы общения на равных. При этом не только педагог может что-то открыть новое ребенку, но и ребенок - педагогу. Задачу общения мы видим в признании и приятии личности ребенка, в развитии речевого общения, в привлечении внимания ребенка к миру, глазам другого, в яркой эмоциональной насыщенности общения детей, в развитии у ребенка умения слушать другого, проявлять доброту и отзывчивость.
Одним из необходимых условий формирования математических представлений также является активизация занятий с детьми. Воспитатели детского сада должны умело варьировать формы и методы обучения. С большим желанием дети будут ждать встреч с воспитателями, которые умеют окружить своих воспитанников добротой, вниманием, создать обстановку взаимного доверия и уважения. Все это должно благоприятно отражаться на развитии математических способностей и эмоциональной сферы дошкольников. Необходимо организовать развивающую среду, где воспитатель должен уделять особое внимание содержанию занятия, так как оно должно удовлетворять потребности актуального, ближайшего и перспективного творческого развития ребенка, становлению его способностей.
Созданная предметная среда должна соответствовать возрастным особенностям детской деятельности, способствовать творческому самовыражению каждого ребенка. Важнейшие условия для поддержания интереса и работоспособности детей – это своевременная смена видов деятельности и разнообразия выполняемых заданий.
Использования наглядности, алгоритма в обучении, когда алгоритм «создается» при активном участии самих детей как условие четкого решения какой-либо игровой или практической задачи.
Дети осваивают умение действовать последовательно в игре. Наиболее успешно этот процесс осуществляется в логико-математических играх, последовательность действий при этом обозначается стрелкой.
Для успешного освоения детьми старшего дошкольного возраста алгоритмов необходимо:
совершенствование умений обозначать предметы, пользуясь заместителями, моделями;
соблюдение последовательности при выполнении игровых и учебных действий (следование за условным знаком-стрелкой);
развитие у детей умения выявлять закономерность в последовательном расположении предметов, действий, выделять и учитывать при этом существенные свойства;
создание условий для самостоятельного составления детьми алгоритмов в разных видах деятельности.
Консультации для воспитателей, методистов, совместные вечера, обсуждение различных проблем на педагогических Советах дают положительные результаты.
Единство содержания обучения и развития будут обеспечивать созданную в группах развивающую предметную среду, продуманная таким образом, что весь материал дает возможность каждому ребенку действовать самому, обеспечивает развитие познавательных интересов и грамотности дошкольников. Необходимо хорошо оборудовать в детском саду мини-лаборатории, дидактический уголок по обучению детей математике.
При соблюдении последовательности при выполнении игровых и учебных (математических заданий) действий дети с удовольствием будут принимать участие в решении. Они будут развивать воображение, наблюдательность. В них будет присутствовать дух соревновательности (кто быстрее, кто правильнее, кто больше знает). Организовать награждение (появиться стимул к игре). В результате дошкольники учатся быстро и логично рассуждать. А главное – в процессе игры дети получают приобретают, формируют знания, испытывая при этом удовольствие. Положительные эмоции способствуют лучшему усвоению изучаемого материала, влияет на развитие личности.
В условиях систематического обучения ребенок может выделять единичное из общего, способен познавать не только общие свойства отдельных предметов и явлений, но и простейшие связи взаимосвязи между ними. Овладение простейшими умственными операциями ведет к более высокому уровню обобщения предметов и явлений по их существенным признакам.
Таким образом, старший дошкольник подходит к осознанию математических отношений.
Содержание программы по развитию элементарных математических представлений предполагает реализацию больших потенциальных возможностей ребенка. Важно, какими методами будет осуществляться обучение.
При определении методов и приемов следует учитывать физические и психические особенности ребенка и вести обучение с помощью дошкольных форм воспитательно-образовательной работы, где широко используются дидактические игры, наглядно-предметные занятия, различные виды практической деятельности. Процесс обучения должен стимулировать активность всех детей, давать возможность спорить, свободно общаться друг с другом в поисках истины.
Наиболее результативным является создание на занятиях психолого-педагогических условий для развития познавательных интересов детей, привлечение их к совместному решению учебных задач, подведение к самостоятельным выводам, включение в занятия проблемных ситуаций.
Главная задача воспитателя на занятиях добиться, чтобы ребенок понимал сущность явлений.
В содержание программы по развитию элементарных математических представлений включен ряд тем, имеющих особое значение для развития у детей мышления, стимулирование их творческих поисков при решении различных учебных задач. Имеется в виду обучение измерению с помощью учебной мерки и деление предметов на несколько равных частей. Данный процесс помогает выявить важные закономерности в вещах и явлениях, скрытые для непосредственного восприятия, способствует формированию логического мышления, умению находить причинные связи, судить по итогу об исходных данных, т.е. дает развивающий эффект.
Важное значение для развития мыслительной активности старших дошкольников имеют ситуации, где они должны самостоятельно найти ответ на поставленный вопрос, опираясь на знания, приобретенные в процессе обучения.
Занятия по математике надо организовывать так, чтобы дети могли свободно общаться, спорить, совместно выполнять задания.
Во время занятий ребенок должен проявлять как можно больше активности, рассуждать, делать «открытия», высказывать свое мнение, не боясь при этом ошибиться. И каждый ошибочный ответ должен рассматриваться не как неудача, а как поиск правильного ответа, решения.
Математика – наука точная. В ней много специальных терминов, которые мы употребляем в работе с детьми. Воспитатель добивается, чтобы ребенок понимал, о чем идет речь, и сам мог грамотно сформулировать свою речь, мысль.
Такого рода исследовательско-лингвистическая работа увлекает ребят, повышает их умственную активность, способствует тому, что сложнейшие математические термины осознаются, а не запоминаются путем зубрежки.
На занятиях по математике следует постоянно обращать внимание на речевую работу. На каждом занятии воспитатель учит ребят четко выражать свою мысль, делать вывод, объяснять, доказывать, использовать полные и краткие ответы. Дети должны понять, что полный ответ необходим, когда надо сделать вывод, умозаключение, объяснить, почему получается тот или иной результат.
Задача речевого развития детей на занятиях по математике успешно решается в дидактических играх с математическим содержанием. Ребенок должен не только быстро, правильно и четко отвечать, но и стремиться быть ведущим, уметь задавать вопросы, когда этого требует игровая ситуация, находить верные слова, чтобы оценить ответ или действия сверстников. Если воспитатель постоянно обращает внимание на речь, корректирует ее, ребята и сами начинают следить за своей речью, она становиться богаче, содержательнее.
В работе с детьми расширен и систематизирован круг геометрических представлений, включены специальные задания, направленные на развитие произвольной памяти и внимания, мелкой моторики кисти руки, зрительно-двигательной координации.
Известный дидакт, одна из ведущих разработчиков проблемы формирования интеллектуального развития в процессе учебы – Щукина Г.И. считает, что интересное занятие можно создать за счет следующих условий:
личности воспитателя (очень часто даже скучный материал, объясняемый любимым воспитателем, хорошо усваивается);
содержания учебного материала (когда ребенку просто нравится содержание данного занятия);
методов и приемов обучения.
Если первые два пункта не всегда в нашей власти, то последний – поле для творческой деятельности любого воспитателя.
Поговорим о некоторых требованиях к современному занятию. С позиций современной педагогической науки следует обратить внимание на следующее:
по возможности стараться на занятии обратиться к каждому дошкольнику не по одному разу, а не менее 3–5 раз, т. е. осуществлять постоянную «обратную связь» – корректировать непонятное или неправильно понятое.
ставить оценку старшему дошкольнику не за отдельный ответ, а за несколько (на разных этапах занятия).
постоянно и целенаправленно заниматься развитием качеств, лежащих в основе интеллектуального развития: быстрота реакции, все виды памяти, внимание, воображение, мышления и т. д. Основная задача каждого воспитателя – не только научить (в нашем случае – математика), а развить мышление ребенка средствами своего предмета.
стараться, когда это, возможно, интегрировать знания, связывая темы своего курса, как с родственными, так и другими учебными занятиями, обогащая знания, расширяя кругозор старшего дошкольника.
Н.А. Менчинская предлагает, что при организации дидактических игр с математическим содержанием необходимо продумывать следующие вопросы методики:
1) Цель игры. Какие умения и навыки в области математики школьники освоят в процессе игры? Какому моменту игры надо уделить особое внимание? Какие другие воспитательные цели преследуются при проведении игры?
2) Количество играющих. Каждая игра требует определенного минимального или максимального количества играющих. Это приходится учитывать при организации игр.
3) Какие дидактические материалы и пособия понадобятся для игры?
4) Как с наименьшей затратой времени познакомить ребят с правилами игры?
5) На какое время должна быть рассчитана игра? Будет ли она занимательной, захватывающей? Пожелают ли ученики вернуться к ней еще раз?
6) Как обеспечить участие всех школьников в игре?
7) Как организовать наблюдение за детьми, чтобы выяснить, все ли включились в работу?
8) Какие изменения можно внести в игру, чтобы повысить интерес и активность детей?
9) Какие выводы следует сообщить учащимся в заключение, после игры (лучшие моменты игры, недочеты в игре, результат усвоения математических знаний, оценки отдельным участникам игры, замечания по нарушению дисциплины и др.)?
Целесообразность использования дидактических игр на различных этапах урока различна. Так, например, при усвоении новых знаний возможности дидактических игр значительно уступают более традиционным формам обучения. Поэтому игровые формы занятий чаще применяют при проверке результатов обучения, выработке навыков, формировании умений. В процессе игры, как уже говорилось, у учащихся вырабатывается целеустремленность, организованность, положительное отношение к учебе.
Определение места дидактической игры в структуре урока и сочетание элементов игры и учения во многом зависят от правильного понимания учителем функций дидактических игр и их классификации. В первую очередь коллективные игры в классе следует разделять по дидактическим задачам урока. Это, прежде всего, игры обучающие, контролирующие, обобщающие.
Обучающей будет игра, если учащиеся, участвуя в ней, приобретают новые знания, умения и навыки или вынуждены приобрести их в процессе подготовки к игре. Причем результат усвоения знаний будет тем лучше, чем четче будет выражен мотив познавательной деятельности не только в игре, но и в самом содержании математического материала.
Контролирующей будет игра, дидактическая цель которой состоит в повторении, закреплении, проверки ранее полученных знаний. Для участия в ней каждому ученику необходима определенная математическая подготовка.
Обобщающие игры требуют интеграции знаний. Они способствуют установлению межпредметных связей, направлены на приобретение умений действовать в различных учебных ситуациях.
Дидактическая игра является средством умственного развития, гак как в процессе игры активизируются разнообразные умственные процессы. Чтобы понять замысел, усвоить игровые действия и правила, нужно активно выслушать и осмыслить объяснение учителя. Решения задач, поставленных играми, требуют сосредоточенного внимания, активной мыслительной деятельности, выполнения сравнения и обобщения.
Таким образом, дидактические игры в зависимости от содержания материала, способа организации, уровня подготовки дошкольников, цели занятия могут приобретать различный характер, например, быть продуктивными, репродуктивными, творческими, конструктивными, практическими, воспитывающими.
Глава II. Опытно-экспериментальная работа по формированию интеллектуального развития старших дошкольников
2.1. Диагностика уровня сформированности интелектуального развития у детей старшего дошкольного возраста
Изучив теоретические вопросы по проблеме интеллектуального развития старших дошкольников, мы приступили к экспериментальной работе.
В эксперименте принимали участие 20 детей в возрасте 5-6 лет МДОУ детский сад №19 г. Белгорода. Эксперимент состоял из 3 этапов: констатирующего, формирующего и контрольного.
Исследование выполнялось в несколько этапов:
1 этап (сентябрь – октябрь 2008 г.) – теоретико-аналитический.
Изучение и анализ психолого-педагогической и методической литературы по теме исследования.
2 этап (октябрь 2008 г. – март 2009 г.) – опытно-экспериментальный.
Проведение констатирующего эксперимента (март 2009 г.).
Проведение формирующего эксперимента (апрель-май 2009 г.).
3 этап (май 2009 г.) – проведение контрольного эксперимента. Анализ и оформление результатов опытно-экспериментальной работы.
Цель констатирующего эксперимента заключается в выявлении уровня сформированности интеллектуального развития старших дошкольников.
Задачи констатирующего эксперимента:
Определить экспериментальную методику обучения, которая бы отвечала особенностям старших дошкольников в системе формирования математических представлений;
.Выявить уровень сформированности интеллектуального развития детей старшего дошкольного возраста в процессе занятий.
Провести диагностического обследования воспитателей с целью выявления насколько компетентно будет осуществляться эффективность процесса обучения дошкольников.
Методические приемы для проведения диагностического обследования ребенка должны быть по возможности краткими - беседы, удобными для быстрого изучения той или иной сферы личности ребенка.
Перед началом диагностического обследования ребенка с целью установления первоначального контакта с ним, рекомендуется проводить беседы, которые могут касаться любой темы. Воспитатель должен хорошо владеть методикой ее проведения.
Беседа с детьми. Обычно она отличается следующей структурой:
а) введение: привлечение ребенка к сотрудничеству «настройка»;
б) свободные, неуправляемые высказывания ребенка;
в) общие вопросы типа: «Ты можешь мне рассказать что-нибудь о себе», «Меня бы интересовало, раз мы уже немного познакомились, с кем ты дружишь?» и т.п.
г) подробное исследование;
е) обращаться к ребенку нужно только по имени.
В педагогическом эксперименте участвовало 20. Из которых 10 человек составили экспериментальную группу и 10 человек - контрольную группу.
| Экспериментальная группа | Контрольная группа |
| Абрамова. А | Белокопытов Д. |
| Белокопытова Т. | Ващенко Д. |
| Бочарникова Э. | Власенко П. |
| Ващекина Э. | Власов Е. |
| Долгова. В. | Гончаренок А. |
| Ивков. С. | Грызя Т. |
| Кононыхин Д. | Концевой М. |
| Малахова. А. | Копенко И. |
| Москалев. А. | Литвинова Е. |
| Павлов. А. | Локтеонова. К. |
На основе анализа психолого-педагогической литературы мы определили критерии уровней формирования навыков интеллектуального развития у старших дошкольников (таблица 1.1.).
Таблица 1.1.
Критерии уровней формирования навыков интеллектуального развития у старших дошкольников (по Беспалько В.П.)
| Уровни | Показатели |
| Высокий уровень | Характерно высокий интеллектуальный уровень: познавательная активность, инициативность, творчество, умение анализировать и делать выводы. Ярко выражено речь ребенка. Имеет познавательный интерес к окружающему миру. Осознают и соотносят свои возможности и навыки с требованиями воспитателя. Развито логическое мышление. |
| Средний уровень | Средний уровень - дети проявляют эрудицию, познавательный интерес, владеют логическим мышлением, но не совсем точно выражает сои мысли, иногда проявляют инициативу в решении упражнений, занятий. Понимают важность занятий, но не всегда ориентируются. В заданиях. |
| Низкий уровень | Для этого уровня характерно низкое интеллектуальное развитие: низкий уровень педагогических знаний и отсутствие логического мышления, речь не связанная, не умеет выразить то, что хочет. |
Для определения уровня формирования интеллектуального развития детей старшего дошкольного возраста к обучению были использованы следующие диагностические методики:
Тест для изучения дифференцированного восприятия «Найди квадрат». (К.Л. Печора, 1978)
Цель: выявить способность к дифференцированному восприятию.
Ребенку показывают рисунок с изображением 10 четырехугольников, среди которых 5 совершенно одинаковых квадратов и 5 четырехугольников, немного отличающихся от квадратов: вертикальные стороны чуть длиннее горизонтальных, или наоборот, какой-либо из углов четырехугольника меньше или больше прямого угла. Ребенку предлагается найти и показать все одинаковые фигуры (квадраты, у которых все стороны и углы равны).
Если ребенок может отыскать все или почти все квадраты, то это свидетельствует о наличии у него способности к дифференцированному восприятию.
Логическое запоминание Тест «Лишний предмет» (Г. Айзенк, 1972)
Цель: оценка образно-логического мышления, умственных операций анализа и синтеза.
Детям предлагается 5 карточек, на которых изображены различные предметы: по 4 на каждой карточке. Мы просили детей определить лишний предмет на карточках, сказать, почему он лишний. После этого предложили каждому ребенку подумать и сказать, как можно назвать оставшиеся 3 предмета одним словом.
Критерии оценки: правильно найти все лишние предметы и назвать обобщенным словом - это высокий уровень образно-логического мышления; если из 5 заданий справились с тремя и назвали обобщенным словом - средний уровень; если неправильных ответов более трех, то ребенок не справился с поставленной задачей - низкий уровень (см. приложение 2).
Познавательный интерес: Тест: «Узнай фигуру». (Р.С. Немов, 2001)
Цель: оценить познавательный интерес и способность к знанию.
Ребенку предлагают посмотреть на картинки, их всего 5. Крайняя слева картинка – образец. Нужно определить и показать, какая из четырех последующих похожа на первую.
Это тренировочная проба, к дальнейшей работе переходите только тогда, когда вы убедитесь, что ребенок понял задание.
Далее показываете ребенку следующие картинки поочередно с первой по десятую.
Эксперимент проводится до тех пор, пока ребенок не решит все десять задач.
Хорошим считается результат, если ребенок справился со всеми задачами за 45 - 60 секунд.
Развитие речи: Тест: «Пиши кружочками» и «Чтение схем – слов» (Г.Г. Григорьева, 1995)
Цель: оценка фонематического слуха.
Предложите ребенку записать несколько слов, но не буквами, а кружочками. Сколько звуков в слове, столько и кружочков.
Например, слово «суп» надо изобразить тремя кружочками:○○○. Проверьте, правильно ли ребенок понял задание. После этого можно приступать к исследованию.
Диктуете ребенку слова, а он записывает их в виде кружочков на листе бумаги.
Набор слов: АУ, РУКА, СОК, ЗВЕЗДА, ВЕСНА.
При правильном выполнении задания, запись должна быть следующей:
Если ребенок выполнил все схемы или четыре из них – это хороший результат. Предложите ребенку картинки, на которых нарисованы животные (лев, белка, корова, слон, кошка) и записаны схемы этих слов в виде кружочков (по количеству звуков в каждом слове).
Задача ребенка заключается в том, чтобы определить, какие кружочки подходят к каждому слову.
Например, слово «волк» соответствует схеме из четырех кружочков, а слово «дом» - из трех. Убедившись в том, что ребенок понял задание, показываете ему рисунок и просите соединить линией картинку с изображением каждого животного с теми кружочками, которые к ней подходят.
Таблица 1.2.
Диагностика интеллектуального развития в процессе формирования первичных математических представлений
| Имя ребенка | Дифференцированное восприятие | Логическое запоминание | Познавательный интерес | Развитие речи |
| Экспериментальная группа | ||||
| Абрамова. А | средний | низкий | средний | средний |
| Белокопытова Т. | низкий | средний | средний | средний |
| Бочарникова Э. | средний | средний | низкий | низкий |
| Ващекина Э. | средний | низкий | средний | средний |
| Долгова. В. | низкий | средний | низкий | низкий |
| Ивков. С. | средний | низкий | средний | средний |
| Кононыхин Д. | низкий | низкий | низкий | средний |
| Малахова. А. | средний | низкий | средний | низкий |
| Москалев. А. | низкий | низкий | средний | низкий |
| Павлов. А. | низкий | средний | низкий | средний |
| Контрольная группа | ||||
| Белокопытов Д. | средний | средний | средний | средний |
| Ващенко Д. | низкий | средний | средний | низкий |
| Власенко П. | низкий | средний | низкий | низкий |
| Власов Е. | низкий | низкий | средний | средний |
| Гончаренок А. | низкий | низкий | низкий | средний |
| Грызя Т. | средний | низкий | средний | средний |
| Концевой М. | низкий | средний | средний | низкий |
| Копенко И. | средний | низкий | низкий | низкий |
| Литвинова Е. | средний | средний | средний | низкий |
| Локтеонова. К. | низкий | средний | средний | средний |
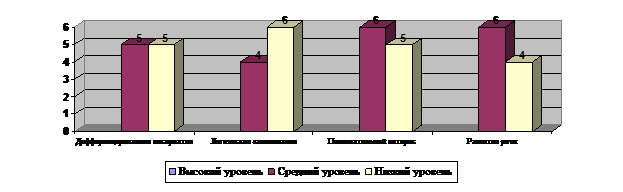
Рис. 1.1. Уровень сформированности интеллектуального развития в процессе математических представлений на констатирующем этапе
в экспериментирующей группе
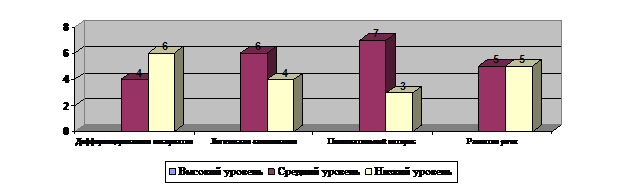
Рис. 1.2. Уровень сформированности интеллектуального развития в процессе математических представлений на констатирующем этапе
в контрольной группе
В начале констатирующего эксперимента провели диагностику. Результаты нашего исследования были следующие. Детей, которые бы задание вообще не принимали, по данным нашего исследования выявлено не было. Поэтому не было и детей с нулевым уровнем развития.
В экспериментальной и контрольной группах в основном имеют как средний, так и низкий уровень.
Таким образом, анализируя результаты констатирующего эксперимента, мы пришли к выводу, что необходимо совершенствовать интеллектуальное развитие старшего дошкольного возраста в процессе формирования первичных математических представлений.
Похожие работы
... футболом, волейболом, подвижными играми. Он может быть применен на базе любых физических упражнений. Таким образом, игровой метод в силу всех присущих ему особенностей используется в процессе физического воспитания не столько для начального обучения движениям или избирательного воздействия на отдельные физические способности, сколько для комплексного совершенствования двигательной деятельности в ...
0 комментариев