Задачі на страхування та їх особливості

2.5. Задачі на страхування та їх особливості

Формування в Україні ринкової економіки та створення різних механізмів ринкових операцій загострює проблеми збереження власних коштів. Зростання ризику у всіх сферах людського життя та господарської діяльності обумовлене необхідністю захисту громадян від можливих витрат та збитків.

Страхування в умовах ринкової економіки ґрунтується на попередньому створенні страхових фондів зі страхових внесків та на відшкодуванні збитків потерпілим. Кожна людина повинна знати, як вона може зменшити свій ризик і скільки їй це коштуватиме. Отже, страхування – це спосіб захисту майнових інтересів громадян в умовах ринкової економіки.

У курсі математики основної школи не можливо висвітлити всі особливості страхової справи, оскільки основні засади страхування пов’язані, в першу чергу, з економічним ризиком, який ґрунтується на поняттях теорії ймовірності. Розділ теорії ймовірності сьогодні не включено до програми основної школи, хоча деякі його засади розкриваються учням лише в старшій школі. Тому ознайомлення з усіма математичними розрахунками страхування в основній школі неможливе, але основні поняття та розрахунки страхування як напрямку фінансової сфери людської діяльності, можуть бути відображені в задачах основної школи.

Страхування як система економічних відносин передбачає наявність двох суб’єктів – страховика та страхувальника. Страховик – це юридична особа (наприклад, акціонерне товариство), яка має право на здійснення страхової діяльності. Страхувальник – це особа, яка страхує власне майно або власні інтереси, сплачує страхові внески та має право на отримання компенсації при настанні страхового випадку.

Законом України “Про страхування” [41] визначено, що об'єктами страхування можуть бути майнові інтереси, що не суперечать законодавству України. Вони пов'язані з:

·           життям, здоров'ям, працездатністю та додатковою пенсією страхувальника або застрахованої особи (особисте страхування);

·           володінням, користуванням і розпорядженням майна (майнове страхування);

·           відшкодуванням страхувальником заподіяної ним шкоди особі або її майну, а також шкоди, заподіяної юридичній особі (страхування відповідальності).

Відповідно розрізняють страхування добровільне та обов’язкове. Добровільне страхування - це страхування, яке здійснюється на основі договору між страхувальником і страховиком. Загальні умови і порядок здійснення добровільного страхування визначаються правилами страхування, що встановлюються страховиком самостійно. Видами добровільного страхування можуть бути: страхування життя; страхування від нещасних випадків; медичне страхування; страхування транспорту; страхування вантажів та багажу; страхування на випадок пожежі та стихійних явищ; страхування майна; страхування кредитів тощо. В Україні здійснюються такі види обов'язкового страхування: медичне страхування; особисте страхування медичних працівників на випадок інфікування вірусом імунодефіциту людини при виконанні ними службових обов'язків; особисте страхування працівників пожежної охорони; страхування спортсменів вищих категорій; страхування життя і здоров'я спеціалістів ветеринарної медицини; особисте страхування від нещасних випадків на транспорті; страхування засобів водного транспорту; страхування врожаю; страхування цивільної відповідальності оператора ядерної установки за ядерну шкоду, яка може бути заподіяна внаслідок ядерного інциденту; страхування працівників, які беруть участь у наданні психіатричної допомоги; страхування тварин; страхування відповідальності суб'єктів туристичної діяльності; страхування відповідальності морського судновласника тощо.

Ознайомлення учнів із різними видами страхування та деякими їх особливостями може бути здійснене за допомогою навчальних математичних задач. Розглянемо, наприклад, такі задачі.

Задача 1. Визначити, яке страхове відшкодування отримає сільськогосподарський виробник, якщо він застрахує урожай за таких умов, що страхова компанія відшкодує збитки у розмірі 70% від недоотримання урожаю. Середня врожайність з 1га - 23 ц, а фактично отримали 20 ц з га. Площа посіву 200га. Закупівельна ціна пшениці за 1 ц дорівнює 50 грн.

Для розв’язання цієї задачі потрібно відповісти на запитання:

1.         Якою повинна бути ціна врожаю?

23 × 200 × 50 = 230 000 (грн.)

2.         Яка фактична ціна отриманого урожаю?

20 × 200 × 50 = 200 000 (грн.)

3.         Яка величина збитків?

230 000 – 200 000 = 30 000 (грн.)

4.         Яке страхове відшкодування?

30 000 × 0,7 = 21 000 (грн.)

Відповідь: 21 000 гривень.

Для слабких учнів можуть бути роздані картки де складений план розв’язування задачі. Сильніші учні самостійно складають план та розв’язують задачу.

Робота з такою задачею не лише вчить учнів обчислювати відсотки від певної фінансової суми, а й показує важливість страхування в реальних умовах життя.

В системі страхування застосовують кілька видів фінансових розрахунків та франшизи.

Для визначення величини страхового внеску в страховій практиці часто використовується страховий тариф, який визначається як ставка страхового внеску з одиниці страхової суми за визначений період страхування.

Задача 6. Страховий внесок за майно становив 300 грн. при страховому тарифі 0,2 %. Яка страхова сума застрахованого майна?

Для розв’язання цієї задачі важливо усвідомити, що страховий тариф показує відсоткове відношення між страховим внеском і страховою сумою, тобто 300 грн. є 0,2 % від страхової суми. Тому знаходження страхової суми полягає у знаходження числа за його частиною:

300 : 0,002 = 150 000 (грн.)

Відповідь: 150 000 грн.

У страхуванні майна найпоширенішим є страхування за дійсною вартістю майна, що визначається на день укладання договору. В цьому випадку страхове забезпечення дорівнює величині збитків, тобто повне покриття збитків страхувальника. Для відображення цього виду страхування під час вивчення теми “ Функція” учням може бути запропоновано задати функціональну залежність між збитками та страховим відшкодуванням і побудувати відповідний графік функції, якщо збитки дорівнюють а грн.

Це завдання не викликає труднощів, але показує механізм фінансових розрахунків у цій ситуації.

Наступний вид розрахунків – страхування за системою пропорційної відповідності. Воно передбачає виплату страхового відшкодування, яке розраховується за формулою 2.10:

, (2.10)

де Q – страхове відшкодування ,

S - страхова сума за угодою (страховий внесок),

T – вартісна оцінка об’єкта страхування,

W – фактична сума збитків.

Це дуже поширений вид страхування. Учням пропонується з формули 2.10 знайти вирази, за яким обчислюється страхова сума за угодою, фактична сума збитків та вартісна оцінка об’єкта страхування. Це знайомить учнів із головними величинами страхової справи та показує математичні залежності між ними.

У 9 класі учням під час вивчення теми “Нерівності” можна запропонувати завдання, яке демонструє використання наведеної вище формули. Наведемо приклад.

Задача 2. Визначити, на яку суму варто застрахувати майно, якщо вартісна оцінка квартири становить 12 000 умовних одиниць, можлива сума збитків 10 000 у. о., а страхове відшкодування повинно бути більше за 8 000 у. о.

Розв’язування цієї задачі можна оформити таким чином.

Складаємо на основі формули 2.10 нерівність:

12 000 × (S/10 000) > 8 000.

Звідси маємо:

S/10 000 > 2/3;

S > 6 666,(6).

Відповідь: бажано застрахувати більше, ніж на 6667 у. о.

В ході аналізу отриманого результату учні спостерігають залежність: покриття збитків тим вище, чим менше різниця між вартісною оцінкою об’єкта страхування та страховою сумою.

Наступний вид – страхування за системою першого ризику. В цьому випадку відбувається виплата відшкодування у розмірі збитків, але в межах страхової суми.

На етапі ознайомлення учнів із задачею, важливо пояснити, що під “першим ризиком” у страховій справі розуміють ризик, вартісна оцінка якого не перевищує страхової суми. При дії даної системи страхування, всі збитки у межах страхової суми відшкодовуються повністю. Збитки, які перевищують страхову суму (другий ризик), страховиком не відшкодовуються. Тому розв’язання цієї задачі полягає у виконанні наступної дії: 321 500 – 234 000 = 87 500 (грн.)

У страховій справі особиста участь страхувальника у покритті збитків виражається через франшизу. Франшиза - частина збитків, що не відшкодовується страховиком згідно з договором страхування, тобто це звільнення страховика від покриття збитків на певну суму. Вона може бути встановлена у відсотках або в абсолютних розмірах щодо страхової суми, вартісної оцінки об’єкту або розміру збитків.

Розрізняють умовну та безумовну франшизи. Умовна франшиза звільняє страховика від відповідальності за збитки, які не перевищують встановленої франшизи і зобов’язує його покривати збитки повністю, якщо розмір їх перевищує франшизу.

Безумовна франшиза звільняє страховика від компенсації перших х % страхової суми, незалежно від величини збитків. За будь-яких умов вона вилучається з зобов’язань страховика, тому вона безумовна. В цьому випадку страхове відшкодування завжди дорівнює різниці між збитками та безумовною франшизою.

Під час вивчення теми “Функції та їх властивості” учням пропонується задати функцію та побудувати їх графік за такими даними задачі:

Задача 4. Задати функціональну залежність між збитками та страховим відшкодуванням, зробити порівняльний аналіз отриманих результатів, якщо:

1.         Страхова сума становить 200 тис. грн., а умовна франшиза становить 20% від страхової суми.

2.         Страхова сума становить 200 тис. грн., а безумовна франшиза становить 20% від страхової суми.

Міркування над даними задачі проводить до наступних результатів.

Нехай х – сума збитків, а у(х) – страхове відшкодування. В умові задачі франшиза становить 200 000 × 0,2 = 40 000 (грн.)

1.         У випадку умовної франшизи повинні виконуватись умови:

·           якщо величина збитків менше за 40000 грн., то страхове відшкодування дорівнює 0, тобто у = 0;

·           якщо величина збитків більше за 40000 грн., то страхове відшкодування дорівнює сумі збитків, тобто у = х.

Врахування цих даних, приводить до такої функції:

В отриманої функції область визначення та область значення лише додатні числа, тому графік функції розташований лише в першій чверті координатної площини. Враховуючи все вище зазначене, отримаємо графік, який зображений на малюнку 2.14.

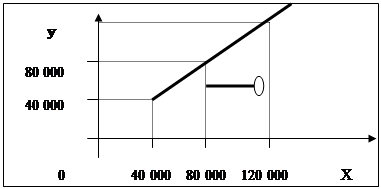
Мал.2.14. Графік страхових відшкодувань у випадку умовної франшизи

2.         У випадку безумовної франшизи страхове відшкодування завжди дорівнює різниці між збитками та безумовною франшизою, тобто .(мал.2.15)

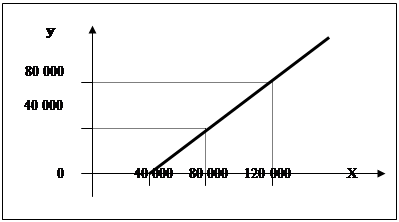
Мал.2.15. Графік страхових відшкодувань у випадку безумовної франшизи

У отриманої функції область визначення та область значення лише додатні числа, тому графік функції розташований лише в перший чверті координатної площини (мал.2.15.)

Проводячи порівняльний аналіз отриманих графіків, треба звернути увагу учнів на відмінності, які виникли з особливостей кожного виду франшизи.

Надалі, учням пропонується самостійно задати числові характеристики для різних видів страхування та побудувати графіки функціональної залежності між збитками і страховим відшкодуванням за цими умовами.

Для узагальнення дій різних видів страхування учням можуть бути запропоновані задачі, де відбувається страхування за декількома видами.

Задача 5. Обчислити страхові відшкодування за викрадений автомобіль вартістю 8200 грн., якщо він був застрахований у трьох різних компаніях на умовах: в першій - на суму 6 500 грн. за безумовною франшизою у розмірі 5 %, в другій - на суму 8 000 грн. за безумовною франшизою у розмірі 3 %, а в третій - на суму 8 100 грн. за умовною франшизою у розмірі 8 %.

В цьому прикладі важливо звернути увагу учнів на те, що у випадку страхування в декількох місцях франшиза обчислюється від відсоткової вартості застрахованого об’єкта, яка попадає на даний договір страхування. Тому обчислення будуть відбуватись за такою схемою:

1.         Загальна страхова сума становить: 6 500+8 000+8 100 = 22 600 (грн.)

2.         Відповідно частки страховиків від загальної суми становлять:

(6 500 : 22 600) × 100 » 28,76 % – для першого,

(8 000 : 22 600) × 100 » 35,40 % – для другого,

(8 100 : 22 600) × 100 » 85,84 % – для третього.

3.         Страхові виплати з врахуванням франшизи становлять:

8 200 × (0,2876 - 0,05) = 1 948,32 (грн.) – для першого,

8 200 × (0,3540 - 0,03) = 2 656,8 (грн.) - для другого,

8 200 × (0,8584 - 0,08) = 6 382,88 (грн.) - для третього.

Відповідь: 1 948,32 грн., 2 656,8 грн., 6 382,88 грн.

Робота з такими даними показує учням особливості, які відбуваються при розрахунках у випадку одночасного страхування одного об’єкта в декількох місцях на різних умовах.

Таким чином, розв’язуючи математичні задачі на страхування учні усвідомлюють такі фінансові поняття, як:

·           страхове відшкодування - страхова виплата, яка здійснюється страховиком у межах страхової суми за договорами майнового страхування і страхування відповідальності при настанні страхового випадку;

·           страхова сума - грошова сума, в межах якої страховик відповідно до умов страхування, зобов'язаний провести виплату при настанні страхового випадку;

·           страховий внесок – сума, яка сплачується страхувальником за страхування;

·           страховий тариф - ставка страхового внеску з одиниці страхової суми за визначений період страхування або відношення страхового внеску до страхової суми об’єкту страхування;

·           вартісна оцінка об’єкта страхування;

·           фактична сума збитків;

·           умовна та безумовна франшиза;

·           інші.

Особливості роботи з задачами на страхування в курсі математики основної школи полягають у трактуванні різних страхових термінів в ході розв’язування задач. Тоді показується математична залежність в страховій системі. Учні вчаться застосовувати математичні знання у звичайних страхових ситуаціях, які відбуваються в повсякденному житті. Важливість страхової справи в умовах ринкової економіки підкреслюється та розкривається змістом математичних задач на страхування, які ми пропонуємо ввести в курс основної школи (додаток Д). Через систему задач на страхування в курсі математики основної школи відбувається ознайомлення учнів з різними страховими поняттями (додаток Є). Задачі на страхування в курсі математики основної школи відображають можливий соціально-фінансовий напрямок захисту власних інтересів кожного громадянина українського суспільства.

Похожие работы

Діагностика і формування пізнавальних здібностей молодших школярів у процесі навчання

Скачать

75833

9

13

... і зусилля для подолання утруднень у процесі виконання завдань, виховання емоційно-позитивного ставлення до навчання); контрольно-оцінний (формування вмінь здійснювати контроль та оцінку своєї навчально-пізнавальної діяльності). [10, 245] Розділ 2. Діагностики та методики формування пізнавальних здібностей молодших школярів   2.1 Особливості пізнавальних здібностей та стану рівня їх розвитку ...

Активізація пізнавальної діяльності на уроках української літератури

Скачать

74270

3

9

... можливість розкрити творчі здібності, удосконалити уміння і навички роботи над теоретичним матеріалом, систематизувати набуті знання тощо. На уроках мови та літератури доцільно використовувати різноманітні ігри, конкурси, змагання, що теж сприяє активізації пізнавальної і розумової діяльності, поглиблює інтерес і увагу школярів, розвиває творчий пошук. Діти дуже люблять ігрові моменти на уроках, ...

Педагогічні основи розвитку процесів запам’ятовування у молодших школярів

Скачать

139453

8

2

... від одного. Без їх розрізнення неможливий і самий процес формування довільної логічної пам'яті у школярів. У сучасний період проблема розвитку процесів запам’ятовування у молодших школярів одержав своє обґрунтування у працях видатних українських вчених та педагогів, проте його переважно розглядають як наскрізний, що пронизує інші дидактичні принципи. Відповідно до логіки навчального процесу (мета ...

Вплив стилю педагогічного спілкування вчителя на процес формування пізнавальної активності старшокласників на уроках загальної біології

Скачать

78069

8

5

... пізнавальну активність учнів у процесі засвоєння знань. Розділ ІІ. Проведення психолого-педагогічного експерименту щодо впливу стилю педагогічного спілкування на пізнавальну активність старшокласників (контингент учнів – 10 клас) та деякі його висновки   2.1 Загально-методичні аспекти проведення психолого-педагогічного дослідження педагогічне спілкування вчитель учень біологія Найдоцільнішим ...