Використання задач на банківські розрахунки в основній школі

2.1. Використання задач на банківські розрахунки в основній школі

Розвиток ринкових відносин розширює сферу діяльності банків. Необхідними чинниками досягнення позитивних результатів у напрямку економічного пожвавлення є свідоме ставлення громадян України до необхідності правового забезпечення стабільного розвитку і діяльності банків в Україні, бо через банківську систему здійснюється основна кількість всіх фінансових розрахункових операцій.

Розуміння актуальності роботи банківської системи сьогодні є необхідною умовою для адаптації громадянина в суспільному житті. Клієнти банків передають йому в управління свої кошти в разі розміщення грошей на депозитних вкладах. Через банки здійснюються розрахунки за надані комунальні послуги, поширеним стає отримання заробітної плати, пенсій та стипендій через розрахунки за допомогою платіжних банківських карт. Послуги банків набувають все більшого поширення та мають велику кількість переваг. Користування такими послугами має бути зрозумілим для пересічних громадян. Виникає необхідність належним чином роз’яснити переваги банківської системи в сфері грошового обігу, захисту власних заощаджень та зручності під час здійснення розрахунків. Основи розуміння особливостей діяльності банків з громадянами (банківського всеобучу) сьогодні можна і необхідно закладати в школі на уроках математики шляхом включення в зміст освіти задач на банківські розрахунки та концентрувати увагу учнів на їх важливості у житті.

Розглянемо звичайну фінансово-математичну проблему, яка сьогодні постає перед багатьма членами нашого суспільства - особливості грошового вкладу в банк. Сьогодні можна знайти деякі задачі з даної тематики у шкільних підручниках, але нажаль їх кількість дуже обмежена і вони не розкривають всіх необхідних аспектів банківської діяльності, з якими зустрічається кожний громадянин та які можуть бути розкриті у курсі математики основної школи.

Одним із видів діяльності банків є виконання валютних фінансових операцій. У нашій країні національною валютою є гривня. Проте часто громадяни України мають справу з такими іноземними валютами, як долар США, російський рубль, євро, японська ієна тощо. Учбові задачі можуть це проілюструвати. Наприклад, в ході ознайомлення учнів дев’ятого класу з темою “Елементи прикладної математики” можливо запропонувати таку задачу:

Задача 1. В таблиці наведені дані про курси гривні встановлені Національним банком України по рокам:

	Кількість гривень за 100 одиниць іноземної валюти
	На 1.11.1997	На 2.11.1998			На 1.11.1999	На 31.10.2000
Німецька марка	103		342	245		233
Японська єна	15		207	245		233
Долар США	187		342	453		543

1) розрахуйте ціну гривні в іноземній валюті кожного року

Методика розв’язання цієї задачі може бути такою. Спочатку учням пропонується самостійно виконати це завдання. Після одержання даних в одній валюті – гривнях, клас колективно виконує вимогу задачі.

Робота з такими величинами привчає учнів до виконання правила порівняння одноімених величин, а також ознайомлює з різними найпоширеними національними валютами світу.

Введення поняття “іноземна валюта” через задачі на уроках математики активізує увагу учнів до запропонованої тематики, розширює їх світогляд та формує знання про іноземну валюту як засіб законного платежу на території відповідної іноземної держави з можливістю вільної конверсії у банківсько-кредитних установах на території України.

У дев‘ятому класі, під час вивчення теми “Відсоткові розрахунки” вчитель може створити проблемну ситуацію, яка збуджує емоції учнів та зацікавлює в пошуку відповіді на таку життєво важливу задачу: “Яка загальна формула нарахування відсоткових грошей в банку, якщо в банк покласти S₀ гривень під р % на n років, а відсотки нараховуються один раз на рік?” Пошук відповіді на це завдання проводить до виведення формул простого та складного відсотку за допомогою послідовних відповідей на такі запитання:

1.         Яка сума нараховується на вклад через 1 рік?

2.         Яка сума з‘являється на вкладі через 1 рік?

3.         Які відсоткові гроші нараховуються на 2-ий рік?

4.         Яким стане вклад через два роки з врахуванням початкової суми вкладу?

Далі, проводячи аналогічні міркування про третій та четвертий роки, учні помічають закономірність між зміною суми вкладу, кількістю років та відсотковою ставкою банку. В результаті, виводяться формули:

 - формула складного відсотку, (2.1)

 - формула простого відсотку, (2.2)

де S_n – сума вкладу після n нарахувань,

S₀ – початкова сума вкладу,

p – відсоткова ставка банку,

n – кількість нарахувань

Для сильних учнів, які знайомі з методом математичної індукції, можна запропонувати довести одержані формули відповідним методом.

Обов‘язково потрібно провести порівняльний аналіз цих формул та звернути увагу учнів на те, що відсотки називають простими, якщо нарахування відбуваються постійно на початковий капітал, а складні відсотки нараховуються на капітал, який утворюється протягом певного періоду.

Особливість нарахувань відсотків щомісячно можна проілюструвати на прикладі:

Задача 3. Обчислити відсоткові гроші у випадку вкладу 1000 грн. під 12 % річних, якщо відсотки нараховуються кожного місяця.

Перед розв’язанням задачі учні колективно шукають відповідь на запитання: Як знайти відсоткову ставку щомісячних нарахувань, якщо відома річна відсоткова ставка?

Для закріплення цього факту учням пропонується за даними задачі відповісти на запитання, якщо відсотки нараховуються кожного півріччя, кожного кварталу, кожного місяця. Після цього можна запропонувати самостійну роботу на виведення формули нарахувань відсоткових грошей, якщо відсотки нараховуються кожного півріччя, кожного кварталу, кожного місяця. Робиться висновок, що під n у формулі розуміється кількість періодів нарахування відсотків.

Для порівняння дії цих формул корисно запропонувати учням самостійно знайти складний відсоток, щоб через три роки на вкладі була така ж сама сума грошей, як і при простому відсотку нарахувань. Таке завдання активізує учнів та вчить порівнювати результати нарахування відсоткових грошей, аналізувати математичні данні.

Сформованість вмінь учнів дев’ятого класу розв‘язувати квадратні рівняння дає змогу розв’язувати задачі, які показують можливе використання послуг банку для власного планування грошових витрат. Це можуть бути, наприклад, задачі такого змісту.

Задача 4. На початку року є можливість внести в банк на рахунок 1640 гривень, але в кінці року треба зняти з рахунку 882 гривні, а через рік знову - 882 гривні. Під який відсоток потрібно внести гроші в банк, щоб вказані операції відбулися?

Початкова робота з даними цієї задачі потребує повторення фінансових понять – початковий вклад, відсоткові гроші, відсоток та прибуток.

Математичні залежності між цими величинами дають можливість пояснити данні задачі у вигляді тверджень: 1640 грн. – початковий вклад для першого року. Нехай х % - щорічні відсоткові нарахування банку. Тоді на кінець року банк нарахував (0,01х×1640) грн., і на рахунку стало

(1 640 + 0,01х × 1 640) грн. або (1 640 × (1 + 0,01х)) грн.

На початку другого року вклад становив

(1 640 × (1 + 0,01х) - 882) грн.

На цю суму було нараховані (0,01х × (1 640 × (1 + 0,01х) - 882)) грн. - відсоткові гроші, а сума, яка була на рахунку на кінець другого року, становила ((1 640 × (1 + 0,01х) - 882) + 0,01х × (1 640 × (1 + 0,01х) - 882)) грн., або ((1640(1+0,01х)-882)(1+0,01х)) грн., що за умовою задачі дорівнює 882 грн.

Отримаємо рівняння:

(1640 × (1 + 0,01х) - 882)(1 + 0,01х) = 882.

Введемо нову змінну у = 1 + 0,01х. Тоді рівняння має вигляд:

(1640у - 882) × у = 882;

1640у² - 882у - 882 = 0;

820у² - 441у - 441 = 0.

Розв‘язуючи отримане квадратне рівняння, знаходимо:

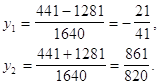
Повертаючись до змінної х, зазначаємо, що значення у₁ не задовольняє умову задачі. Тому 1 + 0,01х =, а х = 5 (%).

Відповідь: 5%.

Методика розв’язування таких задач, як бачимо, традиційна. Це забезпечує успіх у їх використанні. Одночасно з удосконаленням вмінь розв’язувати квадратні рівняння учні здобувають первинні фінансові знання та з’ясовують для себе питання “вдалого” вкладу. Вони шукають найкращий варіант для збереження грошей – можливість отримати потрібний прибуток із певної кількості грошей.

Крім цього учні отримують інформацію і про те, що депозитний вклад - це кошти в готівковій або у безготівковій формі, у валюті України або в іноземній валюті, які розміщені клієнтами на їх іменних рахунках у банку на договірних засадах на визначений строк зберігання або без зазначення такого строку і підлягають виплаті вкладнику відповідно до законодавства України та умов договору [20].

Дуже часто банки пропонують різні види депозитного вкладу. Ознайомлення учнів із особливостями вкладів на депозитний рахунок, як показав експеримент, можна здійснити на уроці математики в 9класі під час вивчення теми “Відсоткові розрахунки”. Для цього учням у ході експерименту було запропоноване попереднє домашнє завдання, яке полягало в знаходженні різних умов вкладів до банків. На уроці було визначено як краще вкласти 1000 гривень на один рік. Кожен учень рахував прибуток, який буде отриманий за один рік, якщо всі гроші відразу покласти до банку та отримувати відсоткові гроші а)щомісяця, б) в кінці дії договору, та якщо вклад поповнювати через певні проміжки часу, наприклад щомісяця або щоквартально. Цікавим прикладом була пропозиція одного з банків про вклад “дитячий”, де банком, крім запропонованих відсоткових грошей, пропонувалась премія при закритті рахунку в термін, обумовлений договором, яка обчислювалась як сума відсоткового доходу, помножена на відсоток, що дорівнює середньому балу успішності.

Таким чином, учні мають можливість познайомитись із особливостями депозитних вкладів у банках та спробувати самостійно здійснити розрахунки кількості власних грошей, які можуть бути покладені на депозитний рахунок.

Різні умови вкладів дають можливість застосовувати фінансові операції, навіть на етапі мотивації вивчення нового матеріалу на уроці. Так, у дев’ятому класі ознайомлення учнів із використанням геометричної прогресії ми провели на прикладі вкладу з обов’язковим поповненням.

Задача 5. Обчислити суму вкладу та прибуток, якщо банк пропонує умови вкладу, відображені в таблиці 2.1, а вкладник планує покласти 1000 гривень на два роки з поповненням по 1000 гривень щоквартально.

 

Таблиця 2.1

Основні умови вкладу (до задачі)

Мінімальна сума вкладу	500 гривень
Мінімальна сума поповнення	100 гривень
Дохідність ( %, річні)		6 місяців	9 місяців	Більше 13 місяців
	До 10000 грн.	10 %	11 %	12 %
	Більше 10000 грн.	12 %	13 %	15,5 %
Нарахування відсотків	Щоквартально
Обов’язкове поповнення	Кожні три місяця

Це задача із зайвими даними. Учні, в першу чергу, повинні прийняти правильне рішення щодо виконання умов банку. Таким чином, для роботи маємо такі данні:

·  Термін дії договору – два роки,

·  Сума вкладу – 1000 гривень із щоквартальним поповненням у 1000 гривень,

·  Відсоток банку – 12 % щорічно, або 12 : 4 = 3 % щоквартально.

Ці данні можуть бути зображені за допомогою мал.2.2 та продемонстровані учням за допомогою кодоскопа.

Мал. 2.2. Виконання умов договору (до задачі)

Аналіз мал.2.2 повинен включати визначення етапів нарахування відсотків. Маємо таку схему нарахування грошей:

·  на останній внесок відсотки нараховується лише один раз, тому з цього внеску вкладник буде мати на кінець дії договору:

1000 + 1000 × 0,03 = 1000 × (1 + 0,03) = 1000 × 1,03;

на шостий внесок (передостанній) відсотки нараховуються два рази, тому з цих грошей на кінець дії договору:

1000 + 1000 × 0,03 + (1000 + 1000 × 0,03) × 0,03 =

1000×(1 + 0,03) + 1000×(1 + 0,03)×0,03 = 1000×(1 + 0,03)(1 + 0,03) = 1000×1,03²;

·  з п’ятого внеску – 1000 × 1,03³, бо відсотки нараховувались три рази;

·  ...

·  з першого внеску – 1000 × 1,03⁸.

Отримали геометричну прогресію, у якої знаменник дорівнює q = 1,03, перший член (останній внесок) b₁= 1000, а кількість членів n =8.

Таким чином, вкладник у кінці дії договору має таку суму грошей:

S =1000×1,03 + 1000×1,03² + 1000×1,03³ +...+ 1000 × 1,03⁸.

Для обчислення значення цього виразу скористаємось формулою суми геометричної прогресії:

 = 8 892,34 (грн.).

Після обчислення значення отриманого виразу, учнів потрібно ознайомити з фінансовими термінами, які використовувались для отримання результату, а саме:

·  ануїтет - послідовність однакових внесків, зроблених через рівні проміжки часу,

·  інтервал сплати – проміжок часу між двома послідовними платежами,

·  строк ануїтету – час, від першого до останнього платежу.

Робота з такими даними показує учням застосування властивостей геометричної прогресії в банківських розрахунках.

При подальшому вивченні властивостей геометричної прогресії може бути розглянута проблемна задача, яка показує діяльність системи банків у нашій державі.

Задача 6. Вклади населення України в комерційних банках з 1995 року в національній валюті кожного року збільшуються приблизно в 2 рази, а у іноземній валюті – в 1,5 рази. В 1995 році вклади населення в комерційних банках в національній валюті становили 505 млн. грн., а в іноземній – 111 млн. грн. Чи буде загальна кількість вкладів утворювати геометричну прогресію, і якщо так, то який у неї буде знаменник?

Розглянемо один з можливих варіантів її розв’язання. Пропонуємо учням заповнити таблицю 2.2 наближених даних по вкладам населення України в комерційних банках з 1995 до 2000 року.

 

Таблица 2.2

Вклади населення України в комерційні банки, млн. грн.

	1995	1996	1997	1998	1999	2000
В національній валюті	505
В комерційній валюті	111
Всього

Для інтенсифікації роботи учнів доцільно заготувати шаблон таблиці та роздати до початку роботи. При цьому початкові данні таблиці можуть мати певні розбіжності, оскільки данні задачі є наближеними до реальних даних, однак не остаточними.

Для активізації пізнавальної діяльності учнів варто заповнення таблиці організувати у вигляді змагання на кращого фінансиста. Далі учням пропонується проаналізувати отримані числа та зробити потрібні висновки.

Заповнення таблиці проводиться кожним учнем самостійно, але аналіз отриманих даних потрібно зробити колективно та звернути увагу учнів на важливість математичних закономірностей у реальному житті. Обов’язково треба звернути увагу учнів на те, що данні про вклади в іноземній валюті наведені в гривнях. Чому?

Якщо роботу проводити на вищому рівні складності, то аналіз задачі приводить до формули загальної кількості всіх вкладів у комерційних банках, тобто:

формула n - ного члена прогресії вкладів у національній валюті - 505×2ⁿ;

формула n - ного члена прогресії вкладів у комерційній валюті - 111×1,5ⁿ.

Тоді формула n - ного члена прогресії всіх вкладів – 505×2ⁿ+111×1,5ⁿ.

Ця задача показує учням, що довіра у людей до роботи з комерційними банками нашої держави поступово зростає. Наведена робота відповідає такому типу проблемних задач, як задача з декількома можливими способами розв’язання.

Отже, при розгляді задач про діяльність банків, яка пов‘язана з депозитними вкладами, потрібно виділити такі величини:

1.         Початковий капітал.

2.         Відсоткова ставка.

3.         Прибуток ( відсоткові гроші).

4.         Термін вкладу (час).

5.         Результативний капітал.

Робота банків не обмежується лише депозитними вкладами, тобто залученням коштів клієнтів із виплатою їм відсоткової ставки. Банки також кредитують клієнтів, тобто надають кошти у користування юридичним або фізичним особам на визначений строк із отриманням прибутку у вигляді процентів, які сплачує клієнт за користування кредитом.

Дуже часто в діяльності банків зустрічається надання коштів у кредит з умовою послідовної виплати суми кредиту за певний проміжок часу.

В нашій державі все більших обертів набирає споживчий кредит, який в свою чергу стає ланкою витрат сімейного бюджету. Споживчий кредит - це кошти та матеріальні цінності, які надаються громадянам для придбання, замовлення та використання товарів (робіт, послуг) для власних побутових потреб на визначений строк та під встановлені проценти. Прикладом отримання споживчого кредиту є кредит на певний проміжок часу з щорічними (щомісячними, щоквартальними) виплатами кредиту та нарахуванням відсотків на суму, яка залишилась не виплаченою. При розгляді властивостей арифметичної прогресії учням запропоновано порівняти величини відсоткових грошей такого кредитування та кредитування, коли відсотки нараховуються завжди на суму кредиту.

Задача 9. Кредит отриманий на 12000 грн. під 10 % річних на залишок кредиту на 12 років з щорічною виплатою 1/12 частини кредиту. На скільки зміняться відсоткові гроші виплати кредиту, якщо взяти цю ж суму на той самий строк під 10 % від суми кредиту?

Для знаходження відповіді на запитання задачі клас доцільно розподілити на дві групи: сильніші учні та слабкі. Для групи з сильніших учнів запропонувати обчислити відсоткові гроші за умови взяття кредиту в задачі, а для групи слабких учнів – за умови запитання задачі.

Міркування сильної групи доцільно спрямувати на складання послідовності щорічних виплат отриманого кредиту:

Кожного року залишок кредиту зменшується на

12 000 × 1/12 = 1 000 (грн.).

Тоді відсоткові виплати за 1 рік становлять

(12 000 – 1 000)×0,1 = 1 100(грн.)

за другий рік – (12 000 – 2 × 1 000)×0,1 = 1 000 (грн.),

за третій рік – (12 000 – 3 × 1 000)×0,1 = 900 (грн.),

...

за одинадцятий рік – (12 000 - 11×1 000)×0,1 = 100 (грн.)

за дванадцятий – 0 грн.

Отже, отримали арифметичну прогресію, різниця якої 100 грн. Тому для обчислення всіх відсоткових грошей скористаємось формулою суми арифметичної прогресії:

 = 6 600 (грн.)

Міркування слабкіших учнів доцільно спрямувати наступним чином: якщо взяти 12000 грн. на 12 років під 10 % річних на суму кредиту, то відсоткові виплати будуть дорівнювати

12 000 × 0,1 = 1 200 (грн.) щорічно,

а років - 12, тому всі відсоткові виплати дорівнюють:

1 200 × 12 = 14 400 (грн.).

Аналіз та порівняння отриманих даних проводиться колективно. Після чого робиться висновок, що виплати більші на

14 400 – 6 600 = 7 800 (грн.).

Також доцільно учням самостійно запропонувати визначити таку відсоткову ставку кредиту без щорічних виплат, щоб відсоткові виплати були однаковими у двох випадках.

Для учнів, які цікавляться математикою, доцільно запропонувати вивести формулу обчислення відсоткових грошей кредиту, який отриманий на S грн. під р % річних на залишок кредиту на n років з щорічною виплатою рівних частин кредиту.

Учні вчаться рахувати власні витрати при використанні різних видів кредитів, які поширені в нашій державі.

У нашій державі існує розгалужена банківська система. Тому найчастіше люди проводять грошові операції зі своїми коштами через декілька різних банків. Так, наприклад, під час вивчення теми "Розв‘язування задач за допомогою рівнянь" учням може бути запропонована така задача.

Задача 10. Яку загальну суму кредитор повинен покласти в три різні банки, щоб виконувались умови: в банк "А" потрібно покласти 45% від вкладу в банк "В", а сума вкладу в банк "В" становить 80% від вкладу в банк "С", а в банк "С" він вклав суму, яка перевищує вклад в банк "А" на 6 400 гривень?

Розв‘язування цієї задачі може бути проведено за такою схемою. Спочатку потрібно звернути увагу учнів на вклади, зроблені в різні банки. За умовою задачі вклади мають між собою математичну відсоткову залежність, хоча в житті бувають різні ситуації і не завжди між банківськими вкладами спостерігається математична залежність або закономірність.

Для перекладу даних задачі на математичну мову, учням самостійно пропонується записати залежність між вкладами в різні банки за допомогою математичних виразів. Виконуючи це завдання, учні приходять до висновку, що для виконання цього завдання доцільно ввести змінну х гривень - сума вкладу в банк "С". Тоді в банк "В" потрібно покласти 0,8х гривень, а в банк "А" - 0,36х гривень. Вклад у банк "С" перевищує вклад у банк "А" на (х - 0,36х) гривень, що за умовою задачі дорівнює 6 400 гривень. Отже, в результаті наведених міркувань отримаємо рівняння з однією змінною:

х - 0,36 × х = 6 400;

0,64 × х = 6 400;

х = 10 000 (грн.).

Тоді вклад у банк "В" дорівнює:

0,8 × 10 000 = 8 000 (грн.),

а вклад у банк "А":

0,36 × 10 000 = 3 600 (грн.).

Загальна сума, вкладена кредитором в банки:

3 600 + 8 000 + 10 000 = 21 600 (грн.).

Підбиваючи підсумковий аналіз цієї задачі, потрібно звернути увагу учнів на велику мережу банків, що працюють в Україні. Вони утворюють дворівневу банківську систему держави (мал.2.4):

Національний банк України

комерційні та спеціалізовані банки

Мал.2.4. Банківська система держави

Національний банк України є головним банком країни. Він проводить єдину кредитно-грошову політику, організовує міжбанківські розрахунки, забезпечує стабілізацію національної валюти та координує роботу всіх комерційних банків. До компетенції комерційних банків віднесено такі функції:

1.         кредитно-розрахункове обслуговування підприємств, організацій, населення;

2.         касове обслуговування підприємств, організацій, населення;

3.         операції з іноземною валютою;

4.         інші, визначені законодавством.

За законом про банки і банківську діяльність [20]кожний комерційний банк зобов’язаний частину коштів відраховувати до Національного банку України для створення стабілізаційного фонду. Це обов‘язкові резерви банків. Вони встановлюються як певний відсоток від суми коштів, якими володіє комерційний банк. Решта коштів – вільний резерв, якими банк розпоряджається самостійно.

Для ілюстрації цього учням може бути запропонована така задача.

Задача 12. Комерційний банк отримав кошти у сумі 650 000 грн., а відсоткова ставка обов‘язкових резервів становить 12%. Знайти вільні та обов‘язкові резерви банку від цієї суми.

Після колективного розв’язання цієї задачі доцільно запропонувати аналогічні данні і провести їх обчислення у формі групової роботи: клас розбивається на групи – банки, назви яким вони придумають самостійно. Ставиться вимога обчислити вільні та обов‘язкові резерви їх банку за умов поданих в табл. 2.4.

 

Таблиця 2.4

Завдання для обчислення резервів банку

№	Банк	Сума надходжень	Відсоткова ставка обов‘язкових резервів
1.		20000	20%
2.		45000	12%
3.		120000	15%
4.		22000	18%
5.		S	p %

Порівнюючи отримані данні, учні роблять висновок, що існує пряма залежність між сумою коштів, які надійшли до банку, та величиною вільних резервів. Як наслідок, кожний банк може видати кредитів не більше за суму його вільних резервів.

Ознайомлення з поняттям обов’язкових резервів банку дає змогу провести дискусію з учнями з питання: "Як Національний банк України впливає на величину кредитів комерційних банків?" В результаті отримаємо відповідь: "Встановленням долі обов‘язкових резервів: чим більше відсоток обов‘язкових резервів, тим менше кредитів може видати банк, і навпаки." Заключним етапом роботи стає виведення загальної формули обчислення обов’язкових та вільних резервів банку, якщо сума вкладу S та відсоткова ставка p % обов‘язкових резервів:

 - обов‘язкові резерви банку, (2.3)

 - вільні резерви банку. (2.4)

Після ознайомлення учнів з основними сторонами діяльності банків у державі, доцільно провести дидактичну гру. Для цього клас слід розподілити на п‘ять команд.

Перша – робітники Національного банку; друга, третя, четверта – різні банки; п‘ята – особи, які співпрацюють із банками. Банки варто назвати та описати отриману банківську систему. Отриманий результат слушно відобразити у вигляді схеми (мал. 2.5.).

 

 

 

 

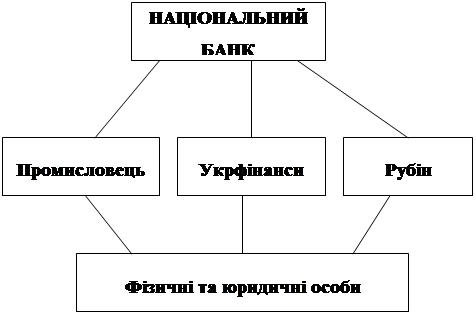
Мал. 2.5. Банківська система на уроці математики

Надалі схему (мал. 2.5) слід доповнити таблицею 2.5.

Завдання на гру.

1. Національний банк встановлює відсоток на обов‘язкові резерви банку, за умови, що кількість обов‘язкових резервів повинна “покривати” половину грошей, які банк бере у фізичних та юридичних осіб на депозитні вклади.

2. Кожна фізична та юридична особа має 3000 гривень. Вони домовляються з одним із банків про депозитний вклад на три роки, а з іншим про кредит на два роки.

3. Кожний банк встановлює власну ставку відсотку на кредит та оформлює договори з фізичними та юридичними особами.

 

Таблиця 2.5

Початкові данні для виконання завдань

Банк	Сума в банку	Сума, яка надійшла на депозитні вклади	Відсоткова ставка депозитних вкладів
Промисливець	15000	7000	16 %
Укрфінанси	17000	10000	20 %
Рубін	14000	5000	14 %

Після оформлення всіх договорів, кожний банк та кожний клієнт банків рахують власний бюджет через три роки.

Національний банк перевіряє обчислення та виносить результати на дошку. Фізичні та юридичні особи, які отримали збитки, шукають варіанти покращення власного стану. Для цього розриваються укладені договори та укладаються нові. Банки, в яких результативна сума буде меншою за початкову, повертають депозитні кошти і надані кредити, а з кожної суми, яка обумовлена договором з клієнтами, виплачує 1 % та починає розрахунки з нової початкової суми.

Діти дуже захоплюються такою діяльністю. Вони набувають нового досвіду у використанні власних коштів при співпраці з банками.

Отже, для розв‘язування математичних задач такого типу цілком досить знань з курсу математики середньої школи. Однак різні поняття та терміни, які зустрічаються в задачах, не є звичними для шкільної програми, тому вимагають додаткового пояснення та обґрунтування. Інколи вони стають зрозумілими вже з тексту задач. Завдяки введенню нових понять розширюються знання учнів та демонструються можливості використання математичних знань у банківській діяльності протягом курсу математики основної школи, що відображено в додатку Є. Це активізує діяльність учнів та збуджує інтерес до практичного застосування шкільних математичних знань.

Ведення задач на діяльність банків до курсу математики основної школи, які пов‘язані з депозитними вкладами та наданням кредитів, ознайомлює учнів із такими фінансовими величинами, як початковий капітал, відсоткова ставка банку, прибуток або відсоткові гроші, термін вкладу або час та результативний капітал. Це показує математичну залежність між ними.

У процесі розв’язування математичних задач на діяльність банків, відбувається усвідомлення учнями таких функцій комерційних банків:

·  кредитно-розрахункове обслуговування підприємств, організацій та населення;

·  касове обслуговування підприємств, організацій та населення;

·  операції з іноземною валютою;

·  інші, визначені законодавством.

Задачі на банківські розрахунки, які були використані в ході експерименту, розширили знання учнів про банківську систему України та розкрили деякі її особливості. Ці задачі рівномірно розподіляються за темами шкільного курсу математики, що відображено в додатку А.