Навигация
Геометрия пространства двойной планетной системы: Земля - Луна
15156
знаков
2
таблицы
4
изображения
И.В. Злобин
Член Финляндской Астрономической Ассоциации,Хельсинки, Финляндия
В данной работе рассмотрен процесс устойчивости Луны на орбите вокруг Земли, с точки зрения геометродинамики. Представлено предложение, в котором формулируется гипотеза о существовании гравитационного "барьера" между Землей и Луной. Методом диаграмм погружения количественно определена высота предполагаемого "барьера" в точке пересечения искривленных метрик; так, высота "барьера" со стороны Луны оценивается величиной 
см , а со стороны Земли 
см. Проведена оценка времени соскальзования Луны со своей орбиты, в результате торможения вызванного излучением слабых гравитационных волн. Оказалось, что 
сек
1. Введение
Задача об устойчивом движении естественного спутника Земли является одной из самых сложных в небесной механике. Это вызвано следующими обстоятельствами: 1) Луна - самое близкое к Земле небесное тело малейшие неправильности в движении Луны могут быть замечены с Земли; 2) изменение положения Луны относительно Земли происходит: во-первых - за счет притяжения ее Землей (основная сила) и во-вторых - за счет того, что Солнце притягивает Луну слабее или сильнее, чем Землю, т.к. Луна оказывается (в процессе движения по орбите вокруг Земли) то ближе, то дальше от Солнца по сравнению с Землей, т.е. вследствие разности сил притяжения Солнцем Земли и Луны; 3) Земля не является точным шаром, она имеет форму - сфероида. Однако, возмущающая сила за счет сжатия не превышает 10 - 6 силы притяжения между Луной и Землей [ 1 ]; 4) Луна перемещается в пространстве по орбите глубоко внутри сферы действия Земли.
Сегодня, теория движения Луны основывается на представлениях ньютоновской механики и оперирует законами классической физики. Использование этих законов позволяет достаточно точно описывать поведение естественного спутника Земли в любой точке на орбите. Ниже будет показано, что пользуясь некоторыми существующими следствиями, вытекающими из геометродинамики, можно по-новому взглянуть на задачу устойчивого движения Луны вокруг Земли.
2. Теоретическая часть.
Прежде, чем перейти к анализу примем ряд допущений: 1) планета Земля и ее естественный спутник Луна - есть по необходимости сферические симметричные системы.. Это обусловленно тем, что можно пренебречь малостью возмущающей силы, которая возникает за счет степени сжатия Земли и Луны. Следовательно, создаваемые этими объектами гравитационные поля должны обладать сферически симметричной топологией; 2) расчет будем проводить для определенного статического положения, т.е. для фиксированной в пространстве и во времени координатной точки расположенной на орбите Луны; 3) квантовыми флуктуациями метрики возникающими вблизи выше указанных объектов пренебрегаем.
Итак, приняв за основу, что Земля и Луна в нашем случае являются сферическими симметричными системами, то к системам такого рода можно применить теорему Биргоффа [2], которая формулируется следующим образом: любая сферически симметричная геометрия некоторой области пространства-времени (являющаяся решением уравнения Эйнштейна в вакууме) с необходимостью является частью геометрии Шварцшильда. Таким образом, сферически симметричное гравитационное поле в пустом пространстве должно быть статическим и описываться метрикой Шварцшильда [3]
, (1)
где
угловой элемент. Причем, здесь принята метрика с сигнатурой (+ ; -;-;-). Так же, понятно, что в данном случае поля тяготения создаются непосредственно Землей и Луной.
Известно, что любая неоднородность в пространстве, вызванная наличием исходных масс, ведет к возмущению пространственно-временной метрики. Вопрос состоит в том, на сколько то или иное тело "деформирует" геометрию пространства? Здесь, следует отметить, что глубина гравитационной ямы прямо пропорциональна массе М стоящей под знаком радикала. Это означает, что для любого текущего значения М можно расчитать параметры гравитационной потенциальной ямы.
Для того, чтобы получить численные значения глубин гравитационных ям, необходимо воспользоваться выводами, вытекающими из геометродинамики [3]. В ее основе лежат законы, которые применяются для анализа сильных гравитационных полей, т.е. для объектов с достаточно большими массами. Задача данного исследования сводится к том, чтобы применить методику применяющуюся в геометродинамики непосредственно к поля тяготения создаваемые Луной и Землей. Законы геометродинамики не ограничивают применения ее правил для анализа слабых гравитационных полей.
Известно, что исходная двойная планетная система Земля-Луна обладает медленным движением и слабым гравитационным полем, это подтверждается неравенствами [4]
(2)
где М - масса системы, R - радиус системы, v - скорость внутри системы, 2GM /с2 - радиус Шварцшильда, с - скорость света. К тому же, как отмечается в [5], из предложения о малой скорости вытекает условие, что само гравитационное поле должно быть слабым. В связи с этим, планета Земля и ее естественный спутник создают вокруг себя искривление пространства-времени, но кривизна метрики будет небольшой.
Сформулируем такое предложение
Для того, чтобы величины 
и 
имели достоверный характер, необходимо и достаточно, получить полное согласование расчетных данных с выводами как с ньютоновской концепцией тяготения, так и с эйнштейновской теорией гравитации.
Для раскрытия сущности Предложения воспользуемся одним из правил геометродинамики, а именно, методом диаграмм погружения. Идея этого метода состоит в том, чтобы для погруженной поверхности [3] с постоянными t и г необходимо найти функцию Z (г) такую, для которой
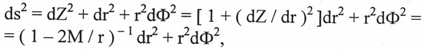(3)
Решение имеет вид
(4)
Соотношение (4) представляет собой параболоид, полученный путем вращения параболы вокруг оси г . В выражение (4) входят: масса объекта М , имеющая размерность - см ; радиус-вектор г - единицы измерения, которого тоже см . Оба этих параметра имеют размерность выраженную через геометризованные единицы [6] .
С физической точки зрения необходимо отметить и такой факт: диаграммы погружения для планет (звезд) строятся, как для внутренних областей, так и для внешних. Но для движущихся частиц (тел) не имеет значения какова геометрия внутри планеты (звезды), поскольку частица (тело) никогда не попадет внутрь планеты (звезды); прежде чем, это произойдет будет наблюдаться процесс столкновения с поверхностью планеты (звезды), разумеется в том случае, если центром притяжения является планета (звезда).
Похожие работы
... собой, их взаимное дополнение друг другом. Недооценивая роль гипотез, как видно из приведенной цитаты Лапласа и из всего его практического творчества, он только отдавал дань духу времени. В области небесной механики Лаплас мог еще обходиться без гипотез, хотя в скрытой форме он должен был нередко ими пользоваться. Араго говорил, что ни один геометр не остерегался так решительно духа гипотез, как ...
... по звездной карте склонение Солнца на данный день и вычисление его высоты в полдень. H = 900 - + = 560 h – высота светила БИЛЕТ № 8 Важнейшие направления и задачи исследования и освоения космического пространства. Основные проблемы современной астрономии: Нет решения многих частных проблем космогонии: · Как сформировалась Луна, как образовались кольца вокруг планет ...
... инерциальных системах отсчета. Пространственно-временной континуум – неразрывная связь пространства и времени и их зависимость от системы отсчета. Тема 11. Основные концепции химии 1. Химия как наука, ее предмет и проблемы Важнейшим разделом современного естествознания является химия. Она играет большую роль в решении наиболее актуальных и перспективных проблем современного общества. К ...
... был «развить плодотворные выводы» на чисто механической основе, отрицая равно и начальный божественный толчок, допускавшийся Ньютоном. Существенный вклад в формирование современной нам астрономической картины мира внес в средние XVIII века первый русский ученый-энциклопедист Михаил Васильевич Ломоносов(1711-1765).Значение вклада Ломоносова в развитии естествознания состояло прежде всего в ...
0 комментариев