Навигация
3. Результаты
Прежде чем, перейти к вопросам расчетного характера, необходимо сказать следующее: т.к. в геометродинамике все величины переводятся в геометризованные единицы, следовательно и здесь необходимо предварительно скорректировать физические параметры Луны и Земли. Для того, чтобы привести физическую массу выше указанных объектов к геометризованной воспользуемся выражением вида [4]
![]() (5)
(5)
где Mgeom - приведенная масса тела, Mphys - физическая масса тела, G - гравитационная постоянная, с - скорость света. Физическая масса Земли и Луны определяются, как ![]() г и
г и ![]() г соответственно. Теперь воспользовавшись (5) оценим приведенные геометризованные массы Луны и Земли:
г соответственно. Теперь воспользовавшись (5) оценим приведенные геометризованные массы Луны и Земли: ![]() см ,
см , ![]() см.
см.
При построении диаграмм погружения, следует учитывать, что текущее значение радиус-вектора r в формуле (4) выбирается в зависимости от величины 2М , т.к. при ![]() имеет место действительная область шварцишльдовской геометрии, а при г < 2М - геометрия становится сингулярной.
имеет место действительная область шварцишльдовской геометрии, а при г < 2М - геометрия становится сингулярной.
Для определения координат диаграмм погружения подставляем ![]() и
и![]() , а так же варьированные значения г в (4) причем дляпростоты расчетов будем выражать текущие значения радиус-вектора через текущие значения приведенных масс Земли и Луны соответственно, см. формулу (4). Полученные результаты занесены в Таблицы 1 и 2.
, а так же варьированные значения г в (4) причем дляпростоты расчетов будем выражать текущие значения радиус-вектора через текущие значения приведенных масс Земли и Луны соответственно, см. формулу (4). Полученные результаты занесены в Таблицы 1 и 2.
Таблица 1
|
|
| |
| см | n | см |
| 0,01090 | 2 | 0 |
| 0,01635 | 3 | 0,0154142 |
| 0,02180 | 4 | 0,0217990 |
| 0,02725 | 5 | 0,0266983 |
| 0,03270 | 6 | 0,0308285 |
| 0,03815 | 7 | 0,0344688 |
| 0,04360 | 8 | 0,0377584 |
| 0,04905 | 9 | 0,0407835 |
| 0,05450 | 10 | 0,0435993 |
Таблица 2
|
|
| |
| см | n | см |
| 0,874 | 2 | 0 |
| 1,311 | 3 | 1,2360226 |
| 1,748 | 4 | 1,6748000 |
| 2,185 | 5 | 2,1408540 |
| 2,622 | 6 | 2,4720453 |
| 3,059 | 7 | 2,7638306 |
| 3,496 | 8 | 3,0276248 |
| 3,933 | 9 | 3,2702085 |
| 4,37 | 10 | 3,4960000 |
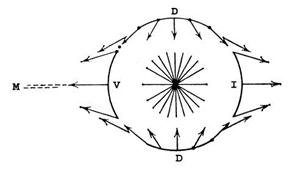
В данном анализе этого достаточно для того, чтобы выявить конфигурацию диаграмм.. На Рисунках 1 и 2 показаны гравитационные "профили" погруженных поверхностей.
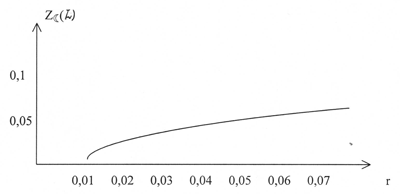
Рис. 1.
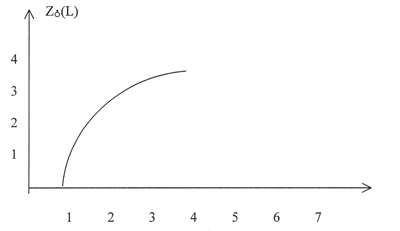
Рис. 2.
Следующим шагом является выявление инвариантности между радиус-вектором г и средним расстоянием L между Землей и Луной. Действительно, радиус-вектор г - это, по суте дела, текущее расстояние от тела до произвольной координатой точки в пространстве. Таким образом, легко заметить, что L тождественно некоторому текущему значению г . Известно, что среднее расстояние от Зумли до Луны оценивается в 384400 км [7]. Запишем L в системе СГС, получаем: ![]() см . Подставляя L в (4) и учитывая соотношение значений
см . Подставляя L в (4) и учитывая соотношение значений ![]() и
и ![]() находим, что глубина гравитационной ямы равна:со стороны Земли
находим, что глубина гравитационной ямы равна:со стороны Земли ![]() см,со стороны Луны
см,со стороны Луны ![]() см.
см.
Следующим этапом является определение координат точки, являющейся местом пересечения двух диаграмм погружения. Обозначим эту точку через А ; примем так же, что А обладает единичной массой mA. Каким свойствам должна подчиняться эта точка:
1) т. А будет располагаться между орбитами Луны и Земли на таком расстоянии, на котором сила тяготения ![]() от Земли до А и сила тяготения
от Земли до А и сила тяготения ![]() от Луны до А - адекватны, т.е.
от Луны до А - адекватны, т.е.![]() ; при этом
; при этом ![]() и
и ![]()
2) т. А располагается на вершине гребня двух пересеченных метрик, т.е. она будет являться наивысшей точкой "барьера", высоту которого обозначим через h.
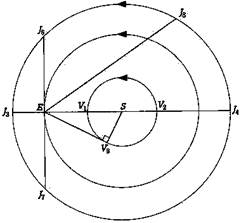
Проведем проработку пунктов 1 и 2 , для этого используем (Рис.3).
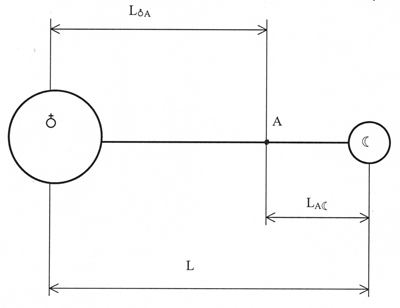
Рис 3.
По пункту 1 запишем закон всемирного тяготения для т. А , Земли и Луны. Имеем:
со стороны Земли![]() (6)
(6)
со стороны Луны![]()
С учетом равентсва этих сил, получим
![]() (7)
(7)
где ![]() - гравитационная постоянная;
- гравитационная постоянная; ![]() г - физическая масса Земли,
г - физическая масса Земли, ![]() г - физическая масса Луны; mA - единичная масса т. А ;
г - физическая масса Луны; mA - единичная масса т. А ; ![]() - расстояние от Земли до т. А ;
- расстояние от Земли до т. А ; ![]() - расстояние от т. А до Луны. Так как
- расстояние от т. А до Луны. Так как![]() , следовательно выражение (7) перепишется в виде
, следовательно выражение (7) перепишется в виде
![]() (8)
(8)
Это соотношение разрешимо относительно![]() , если
, если![]() ;
;![]() .После преобразований находим, что
.После преобразований находим, что
![]() (9)
(9)
Отсюда ![]() см . И тогда
см . И тогда ![]() см . Проверка: в выражение (6) подставляем
см . Проверка: в выражение (6) подставляем ![]() и
и ![]() и выясняем, что
и выясняем, что![]() ;
;![]() . Видно, что значения гравитационных сил согласуется до четвертого знака после запятой.
. Видно, что значения гравитационных сил согласуется до четвертого знака после запятой.
Теперь, остается подставить ![]() и
и![]() , которые тождественны г , в (4) , чтобы определить величину параметра h , указанного в пункте 2) . Таким образом, со стороны Луны т. А располагается на высоте
, которые тождественны г , в (4) , чтобы определить величину параметра h , указанного в пункте 2) . Таким образом, со стороны Луны т. А располагается на высоте![]() , а со стороны Земли
, а со стороны Земли ![]() смПерейдем теперь к вопросу, который касается проблемы связанной с процессом гравитационного излучения исходной двойной системы. Естественно ожидать, что при тех параметрах, которыми обладает двойная планетная система Земля-Луна полная энергия излучения Е и мощность Р будут определяться весьма малыми значениями. В данной работе не проводятся численные оценки этих параметров, ибо это не входит в задачу данного исследования. Здесь, просто, констатируется выше указанный факт.
смПерейдем теперь к вопросу, который касается проблемы связанной с процессом гравитационного излучения исходной двойной системы. Естественно ожидать, что при тех параметрах, которыми обладает двойная планетная система Земля-Луна полная энергия излучения Е и мощность Р будут определяться весьма малыми значениями. В данной работе не проводятся численные оценки этих параметров, ибо это не входит в задачу данного исследования. Здесь, просто, констатируется выше указанный факт.
Из всего комплекса характеристик описывающих процесс гравитационного излучения двойной системы, заслуживает внимание только время t, через которое расстояние между Землей и Луной уменьшится до нуля [3]
![]() (11)
(11)
где L - расстояние между Землей и Луной; ![]() - масса, равная
- масса, равная
![]() - масса, равная
- масса, равная
![]() . Учитывая их численные значения, которые указаны в (5), находим
. Учитывая их численные значения, которые указаны в (5), находим![]() см . Используя калибровку вида [4]
см . Используя калибровку вида [4]
![]() (12)
(12)
определяем, что время, выраженное в физических единицах, при котором расстояние между Луной и Землей уменьшится до нуля, равно ![]() сек . Таким образом, двойная планетная система Земля-Луна будет устойчива на большом временном промежутке, даже в случае излучения слабых гравитационных волн.
сек . Таким образом, двойная планетная система Земля-Луна будет устойчива на большом временном промежутке, даже в случае излучения слабых гравитационных волн.
Согласно предложенному сценарию строения межпланетной геометрии пространства двойной системы Земля-Луна, наблюдаем следующую картину (Рис. 4).
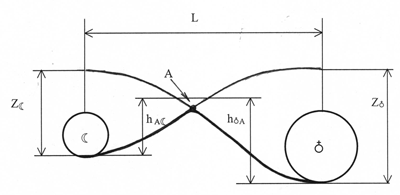
Рис.4
Пусть, некоторое пробное тело движется от Земли к Луне. Тогда, оно будет подниматься по геодезической из потенциальной гравитационной ямы ![]() Земли по направлению к вершине "барьера" метрики (т. А). По мере движения вверх по "барьеру" пробное тело испытывает уменьшение воздействия поля тяготения Земли. На вершине "барьера" действие гравитационных сил со стороны Луны и Земли одинаково. Соскальзывая с "барьера" (процесс погружения ), пробное тело все больше захватывается потенциальным гравитационным полем Луны. Спустившись с "барьера" метрики оно оказывается в гравитационной яме
Земли по направлению к вершине "барьера" метрики (т. А). По мере движения вверх по "барьеру" пробное тело испытывает уменьшение воздействия поля тяготения Земли. На вершине "барьера" действие гравитационных сил со стороны Луны и Земли одинаково. Соскальзывая с "барьера" (процесс погружения ), пробное тело все больше захватывается потенциальным гравитационным полем Луны. Спустившись с "барьера" метрики оно оказывается в гравитационной яме![]() , созданной Луной.
, созданной Луной.
4. Заключение.
В данной работе, используя методику диаграмм погружения, были определены: 1) глубины потенциальных гравитационных ям создаваемые Землей и Луной соответственно; 2) найдены конкретные значения высоты пространственного "барьера", как со стороны Луны -![]() , так и со стороны Земли -
, так и со стороны Земли -![]() . Как и предполагалось, эти числовые характеристики малы в соизмерении, как с расстоянием L между Землей и Луной, так и с самими размерами этих тел [4] (радиус Земли равен
. Как и предполагалось, эти числовые характеристики малы в соизмерении, как с расстоянием L между Землей и Луной, так и с самими размерами этих тел [4] (радиус Земли равен ![]() см, а радиус Луны -
см, а радиус Луны - ![]() см). Этот факт находится в хорошем согласии с механикой Ньютона, которая применяется для анализа слабых источников гравитационных полей.
см). Этот факт находится в хорошем согласии с механикой Ньютона, которая применяется для анализа слабых источников гравитационных полей.
Возможно, наличие "барьера" метрики между Землей и Луной в дополнительной степени способствует устойчивости в пространстве исходной двойной планетной системы. Хотя высота этого "барьера" и незначительна, но Луна, просто не может преодолеть этот "барьер" без внешнего притока дополнительной энергии, такой, при которой Луна смогла бы подняться на вершину "барьера" и скатиться по искривленному профилю метрики в центр потенциальной гравитационной ямы создаваемой Землей.
Отсутствие же "пространственного барьера", по всей видимости, может привести к неустойчивому состоянию двойной планетной системы Земля - Луна . Отмечается так же, что найденные параметры ![]() и
и ![]() будут необходимы для более тонких оценок физико-геометрического состояния искривленного пространства в выше указанной системе.
будут необходимы для более тонких оценок физико-геометрического состояния искривленного пространства в выше указанной системе.
Отметим так же, что предложенное в данном работе исследование не подменяет собой строгие классические выводы объясняющие устойчивое положение на орбите естественного спутника Земли. Оно позволяет глубже взглянуть на механизм гравитационной связанности Луны и Земли.
И в окончании, хотелось бы отметить два чрезвычайно важных следствия, которые вытекают из анализа представленного в данной статье:
1) так как, Луна движется вокруг Земли по эллиптической орбите, т.е. имеется апогей (406700 км) и перигей (356400км), то легко заметить, что высота гравитационного "барьера" h будет варьироваться от min до max величины. Причем min высота достигается при апогее, a max - при перигее. Численные значения планируется получить в новом исследовании;
2) аппроксимируя методику диаграмм погружения в целом на всю Солнечную систему можно точно построить гравитационный профиль нашей планетной системы, что, так же, в перспективе найдет отражение в будущих работах.
Список литературы
Ю.А. Рябов, Движение небесных тел, Наука, Москва (1977).
G. D. Birkhoff, Relativity and modern physics, Mass., Harvard University Press, Cambridge, (1923).
А. Лайтман, В. Пресс, Р. Прайс, С. Тюкольский, Сборник задач по теории относительнотси и гравитации, пер. с англ. А. П. Бондарев и Ю. А.Данилов, под ред. И. М. Халатникова, Мир, Москва, (1979).
К. R. Lang, Astrophysical formulae, Part 2, Springer-Verlad , Berlin, Heidelberg, New York, (1974)
Л. Д. Ландау, Е. М. Лифшиц, Теория Поля, Наука, Москва, (1973).
С. W. Misner, К. S. Thorn, J. A. Wheeler, Gravitation, W. H. Freeman, New York, (1973).
М. У. Сагитов, Лунная гравиметрия, Наука, Москва, (1979).
Похожие работы
... собой, их взаимное дополнение друг другом. Недооценивая роль гипотез, как видно из приведенной цитаты Лапласа и из всего его практического творчества, он только отдавал дань духу времени. В области небесной механики Лаплас мог еще обходиться без гипотез, хотя в скрытой форме он должен был нередко ими пользоваться. Араго говорил, что ни один геометр не остерегался так решительно духа гипотез, как ...
... по звездной карте склонение Солнца на данный день и вычисление его высоты в полдень. H = 900 - + = 560 h – высота светила БИЛЕТ № 8 Важнейшие направления и задачи исследования и освоения космического пространства. Основные проблемы современной астрономии: Нет решения многих частных проблем космогонии: · Как сформировалась Луна, как образовались кольца вокруг планет ...
... инерциальных системах отсчета. Пространственно-временной континуум – неразрывная связь пространства и времени и их зависимость от системы отсчета. Тема 11. Основные концепции химии 1. Химия как наука, ее предмет и проблемы Важнейшим разделом современного естествознания является химия. Она играет большую роль в решении наиболее актуальных и перспективных проблем современного общества. К ...
... был «развить плодотворные выводы» на чисто механической основе, отрицая равно и начальный божественный толчок, допускавшийся Ньютоном. Существенный вклад в формирование современной нам астрономической картины мира внес в средние XVIII века первый русский ученый-энциклопедист Михаил Васильевич Ломоносов(1711-1765).Значение вклада Ломоносова в развитии естествознания состояло прежде всего в ...


0 комментариев