Навигация
Определение ускорений точек и звеньев механизма
1.2.2 Определение ускорений точек и звеньев механизма
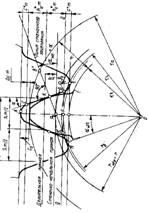
Для определения ускорений точек и звеньев механизма воспользуемся методом планов ускорений. Построение планов ускорений начинаем с ведущего звена механизма AB. Поскольку wAB = const , то ускорение точки А :
aA=w AB 2×lAB = 892 ×0,034 = 269,3 м/с2 (1.2.20).
Ускорение точки A направлено вдоль звена АB к центру его вращения. С любой произвольной точки, в дальнейшем называемой полюсом плана ускорений Па, отложим вектор длиной 134,65 мм параллельно звену АВ. Конец вектора обозначим точкой а’. Масштабный коэффициент ускорений ![]() mа найдём таким образом:
mа найдём таким образом:
![]()
mа=aА / Паа’ = 269,3 /134,65 = 2 м/мм×с2 (1.2.21),
где ПАВ – длина вектора AB на плане ускорений.
Ускорение точки C можно найти из условия принадлежности этой точки двум звеньям: АС и СD. Оба звена выполняют плоско-параллельное движение. Запишем уравнение плоско-параллельного движения звена АС :
аС=aА+anАС+atАС (1.2.22).
В этой векторной сумме первое составляющее известно, а ускорение anАС - направлено из точки А в точку С вдоль звена и численно равно:
anАС=V2АС/lAC=(mV ×ac)2/ lAC=(0,02 × 12)2/0,09 = 0,64 м/с2 (1.2.23).
Длина соответствующего отрезка на плане ускорений:
nАС=anАС/mа= 0,64/2 = 0,32 мм (1.2.24).
На плане ускорений проводим вектор из точки а’ вдоль звена АС длиной nАС = 0,32 мм. Про третье составляющее векторного уравнения, так называемое ускорение звена АС тангенциальное, известно лишь его направление - перпендикулярно звену. Потому на плане ускорений перпендикулярно звену nАС из его конца проводим перпендикуляр.
Принадлежность точки С звену СD дает возможность записать уравнение:
аС=aD+anСD+atСD (1.2.25).
Точка D является неподвижной, ее ускорение равно 0, на плане ускорений точка d’ находится в полюсе Па.
Скалярное значение вектора anСD определяется из соотношения:
anСD=V2CD/lCD=(mV ×cd)2/ lCD=(0,02 × 152)2/0,06 = 154,02 м/с2 (1.2.26).
Длина соответствующего отрезка на плане ускорений:
nСD=anDС/mа= 154,02/2 = 77 мм (1.2.27).
К точке d’, которая находится в полюсе, достраивается вектор длиной nСD= 77мм, по направлению параллельный звену СD, а из его конца проводится вектор, который перпендикулярен ему, и соответствует третьей составляющей векторного уравнения - atСD. На пересечении линий atАС и atСD находится точка с’. Чтобы найти ускорение точки с’ соединим ее с полюсом Па. Численно значение ускорения точки С равно:
аС = mа · Па c’ = 2 · 86 = 172 м/с2 (1.2.28).
где Па c’ - длина вектора, который соединяет полюс с точкой с’.
Точку е’ можно найти на отрезке a’c’ из соотношения:
lАС / lЕС = а’с’ / е’с’. (1.2.29),
е’с’ = 30 · 54 / 90 = 18 мм .
где lЕС - длина звена ЕС;
е’с’ - длина вектора на плане ускорений.
Соединим найденную точку е’ с полюсом, чтобы получить ее численное значение:
аЕ = mа · Па е’ = 2 · 100 = 200 м/с2 (1.2.30),
где Па е’ - длина вектора, который соединяет полюс с точкой е’.
Найдем местоположение на плане ускорения точки F. Для этого составим уравнение плоско-паралельного движения звена EF относительно точки Е:
аF=aE+anEF+atEF (1.2.31).
Нормальное ускорение anEF звена ED найдем следующим образом:
anEF=V2EF/lEF=(mV×ef)2/ lEF=(0,02 × 136)2/0,11 = 67,25 м/с2 (1.2.32),
длина соответствующего вектора на плане ускорений составляет:
nEF=anEF/mа= 67,25/2 = 33,62 мм (1.2.33).
На плане ускорений из точки е’ проводим вектор nEF, параллельный звену EF и направленный от E к F, а с конца этого вектора перпендикуляр, который соответствует направлению atEF . Для исследования движения ползуна необходимо использовать точку F0 на неподвижной направляющей. Тогда уравнение движения точки F:
аF=aF0+aFF0 (1.2.34).
Так как точка F0 неподвижна, то на плане ускорений точка f0’ находится в полюсе. Про ускорение aFF0 известно лишь то, что оно параллельно направляющей. Потому на плане через точку f0’ строится горизонтальная линия. На пересечении этой линии и линии atEF находится точка f’. Численное значение ускорения точки F:
аF = mа · Па f’ = 2 · 63 = 126 м/с2, (1.2.35),
где Па f’ - длина вектора, который соединяет полюс с точкой f’.
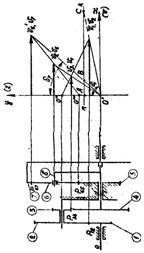
Расставим на плане ускорений центры масс каждого звена данного механизма. Для звена BA вектор центра масс S1’ на плане скоростей будет направлен из полюса вдоль вектора b’a’ величиной равной его половине.
Численное значение ускорения аS1 равно:
аS1 = mа · Па S1’ = 2 · 67 = 134 м/с2 (1.2.36).
Для звена АС вектор его центра масс S2 на плане ускорений будет направлен из полюса в точку соответствующую середине отрезка а’с’.
Численное значение ускорения аS2 равно:
аS2 = mа · Па S2’ = 2 · 109 = 218 м/с2 (1.2.37).
Вектор центра масс S3 звена ЕF на плане ускорений будет направлен из полюса в точку соответствующую середине отрезка е’f’ на плане ускорений.
Численное значение ускорения аS3 равно:
аS3= mа · Па S3’ = 2 · 82 = 164 м/с2 (1.2.38).
Для звена DC вектор центра масс S4 на плане ускорений будет направлен из полюса вдоль вектора d’c’ величиной равной его половине.
Численное значение ускорения аS4 равно:
аS4= mа · Па S4’ = 2 · 43 = 86 м/с2 (1.2.39).
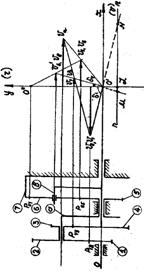
С помощью плана ускорений можно определить угловые ускорения звеньев механизма. Угловое ускорение звена АС равно:
εАС = аtAC/ lAC = mа · tAC/ lAC = 2 · 53/ 0,09 = 1177,77 рад/с2(1.2.40)
где lAC - длина звена; аAC- ускорение движения точки А относительно точки С. Аналогично для звена EF вычислим его угловое ускорение εEF:
εEF = аtEF/ lEF = mа · tEF/ lEF = 2 · 35/ 0,11 = 636,36 рад/с2(1.2.41)
Таким же образом для звена СD вычислим его угловое ускорение εCD:
εCD = аtCD/ lCD = mа · tCD/ lCD = 2 · 37/ 0,06 = 1233,33 рад/с2(1.2.42).
Угловое ускорение звена АВ εАВ = 0.
Полученные при построении плана ускорений данные сведем в таблицу 1.2.
Таблица 1.2
| аA = 269,314 м/с2 | aS1 = 134 м/с2 | εАВ = 0 рад/с2 |
| аС = 172 м/с2 | aS2 = 218 м/с2 | εАС = 1177,77 рад/с2 |
| аЕ = 200 м/с2 | aS3 = 164 м/с2 | εСD = 1233,33 рад/с2 |
| aF = 66 м/с2 | aS4 = 84 м/с2 | εEF = 636,36 рад/с2 |
Похожие работы
... длину вектора и переведем ее обратно: = 79 мм = 2370 Н 2. ПРОЕКТНЫЙ РАСЧЕТ ЗВЕНЬЕВ МЕХАНИЗМА НА ПРОЧНОСТЬ 2.1 Выбор расчетной схемы В результате динамического анализа плоского рычажного механизма были определены внешние силы, которые действуют на каждое звено и кинематическую пару. Такими внешними силами являются силы инерции , моменты инерции и реакции в кинематических парах R. Под ...
... Отсюда: H (1.48) Н.м (1.49) Полученные данные занесем в таблицу 1.4. Таблица 1.4 Fур, Н Мур, Н×м 28 0.7 2. ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими внешними усилиями ...
... 74 R05 24.4 0,005 G4 14,7 Fi4 7.02 R04 7.6 G5 24,5 Fi5 8.125 Fур 0,197 2 ПРОЕКТНЫЙ РАСЧЕТ МЕХАНИЗМА НА ПРОЧНОСТЬ В результате динамического анализа плоского рычажного механизма были определены внешние силы, действующие на каждое звено и кинематическую пару. Этими ...
... говорит о том, что механизм не вращается. Но на самом деле он вращается, но есть пассивная связь EF, не добавляющая степеней свободы механизму. Аналитический метод кинематического исследования механизмов. Аналоги скоростей и ускорений Кинематическое исследование механизма, т.е. изучение движения звеньев механизма без учета сил, обусловливающих это движение, состоит в основном в решении трех ...
0 комментариев