СИЛОВОЙ АНАЛИЗ МЕХАНИЗМА

1.3 СИЛОВОЙ АНАЛИЗ МЕХАНИЗМА

Кинетостатический расчет, положенный в основу силового расчета механизма, базируется на принципе Д’ Аламбера, который в общем случае движения звеньев механизмов, совершающих сложное плоское движение, позволяет решить задачу путем сведения сил инерции звеньев к главному вектору инерции Fi и к главному моменту сил Мi.

Fi = - a_si· m_i (1.3.1).

 

Знак "-" означает, что вектор силы инерции направлен в сторону противоположную ускорению центра масс.

Массы звеньев рассчитываются с помощью формулы:

m = q · l (1.3.2),

 

где q = 0,1 кг/м, l - длина звена.

m = P/g (1.3.3),

 

где g- ускорение свободного падения, g = 9,8 м/с²

Также существует главный момент инерции звена, который приложен к центру масс звена и направлен в противоположную сторону угловому ускорению звена.

М_i= -J_si · ε (1.3.4),

 

где J_s- момент инерции звена,

ε - угловое ускорение звена.

1.3.1 РАСЧЕТ СИЛ И ГЛАВНЫХ МОМЕНТОВ ИНЕРЦИИ ЗВЕНЬЕВ МЕХАНИЗМА

m_EF = q · l_EF = 0,1 · 0,11 = 0,011 кг;

а_S3 = 164 м/c²;

F_i1 = - a_s1 · m_AB = - 164 · 0, 011 = - 1,8 Н;

J_S3 = m_EF · l_EF² / 12 = 0,011 · (0,11)² /12 = 11 · 10^-6 кг · м²

ε = 636,36 рад/с²

M_u3 = - J_S3 · ε = 11 · 10^-6 · 636,36 = -0,7 · 10^-2

m_АС = q · l_AC = 0,1 · 0,09 = 0,009 кг;

а_S2 = 218 м/c²;

F_i2 = - a_s2 · m_AC = - 218 · 0, 009 = -1,9 Н;

J_S2 = m_AC · l_AC² / 12 = 0,009 · (0,09)² /12 = 6 · 10^-6 кг · м²

ε = 1177,77 рад/с²

M_u2 = - J_S2 · ε = - 6 · 10^-6 · 1177,77 = - 0,7 · 10^-2

m_CD = q · l_CD = 0,1 · 0,06 = 0,006 кг;

а_S4 = 86 м/c²;

F_i4 = - a_s4 · m_CD = - 86 · 0, 006 = - 0,5 Н;

J_S4 = m_CD · l_CD² / 12 = 0,006 · (0,06)² /12 = 1,8 · 10^-6 кг · м²

ε = 1233,33 рад/с²

M_u4 = - J_S4 · ε = 1,8 · 10^-6 · 1233,33 = -0,2 · 10^-2

m_AB = q · l_AB = 0,1 · 0,034 = 0,0034 кг;

а_S1 = 134 м/c²;

F_i1 = - a_s1 · m_AB = - 134 · 0, 0034 = - 0,45 Н;

Силы и главные моменты звеньев сведем в таблицу 1.3.

Таблица 1.3

Fi1 = - 0,45 H	Mi1 = 0 H · м2
Fi2 = - 1,9 H	Mi2 =- 0,7· 10-2 H · м2
Fi3 = - 1,8 H	Mi3 =- 0,7· 10-2 H · м2
Fi4 = - 0,5 H	Mi4 =- 0,2· 10-2 H · м2

1.3.2 ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В КИНЕМАТИЧЕСКИХ ПАРАХ

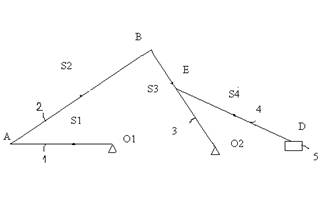
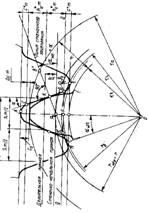
Силовой анализ механизма начинаем с группы Ассура 3-5, наиболее удаленной от ведущего звена. Связи в шарнирах заменяются реакциями R_E1 и R_E2.

В шарнире F реакция неизвестна по модулю и направлена по горизонтали. Обозначим в точке S₃ силу инерции. Обозначим также вес G₃ звена FE и вес ползуна P.

Сумма моментов относительно точки F равна 0:

∑ M_F = 0 (1.3.4)

∑ M_F = -R’_E · l_ef + F_i3 · h _i3 - M + G₃h₁ = 0 (1.3.5)

R’_E =(G₃h₁ + F_i3 · h _i3 - M) / l_ef = (0,1 ·0,008 +1,8·0,006 +0,7·10^-2) / 0,11 = 0,1 H

 

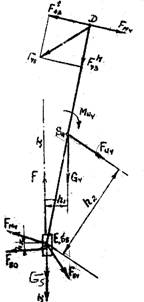
Составляем векторное уравнение:

G₃ + R’_E+ R"_E+ F_i3 + F_i5 + P + G₅+R₅₆ = 0 (1.3.6).

 

С учетом этого уравнения строим замкнутый силовой многоугольник. На чертеже выбираем полюс P_F. От него проводим вектор произвольной длины по направлению силы G_3. Вычисляем масштабный коэффициент:

 

μ_F = G₃ / P_F G₃ (1.3.7),

 μ_F = 0,1/ 5 = 0,02 Н/мм

 

Далее к вектору G₃ достраиваем другие составляющие уравнения (1.3.6), рассчитывая длину векторов при помощи масштабного коэффициента. Находим неизвестные силы R’’_Eи R₅₆, зная их направление. Определив их численное значения в мм, переводим это значение в Н с помощью масштабного коэффициента.

R’’_E = m_F· П_F R’’_E = 0,02 · 84= 1,68 H (1.3.8),

 

где, П_F R’’_E - положение R’’_Eна плане сил.

 

R₅₆= m_F· П_F R₅₆ = 0,02 · 37,5 = 0,75 H (1.3.9),

 

где, П_F R₅₆- положение R₅₆ на плане сил.

Найдем R_E- результирующую силу в паре Е, соединив начало R’_Eи конец R"_E. Определив его численное значения в мм, переводим это значение в Н с помощью масштабного коэффициента.

R_E = m_F· П_F R_E = 0,02 · 85= 1,7 H (1.3.10),

 

где, П_F R_E - положение R_E на плане сил.

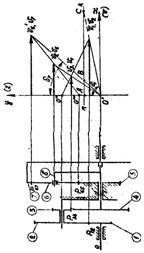
Для определения реакции в кинематической паре 2-4 к шарниру АС необходимо приложить силу R_Eтого же значения, но противоположного направления. Реакции в шарнирах А и D нужно разложить на составляющие по направлению осей R’_А и R’_D, и перпендикулярные к ним: R’’_А и R’’_D. Известна точка приложения сил - центр шарнира, запишем уравнения сумм моментов каждого звена относительно точки С.

∑ M_С = R’_А · l_АС - F _i2 · h _i5 + M_i2 - G₂h₆ + R_E = 0 (1.3.11),

R’_A =(- G₂h₆ - F_i2 · h _i5 + M _i2) / l_AC= (-0,09·0,036 +1,9·0,023 - 0,7·10^-2) / 0,09 = 1,9 H

 

Для звена СD сумма моментов относительно точки С равна нулю.

∑ M_С = R’_D · l_DС + F _i4 · h _i3 + M_i4 + G₄h₄ = 0 (1.3.12),

R’_D = (- F _i4 · h _i3 - M_i4 - G₄h₄) / l_DС = (0,5 · 0,012 + 0,2·10^-2 - 0,06 · 0,02) / 0,06 = 0,1 H

 

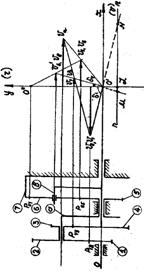
Рассмотрим уравнение равновесия группы в целом. Запишем векторное уравнение равновесия этой группы:

R’_D+ R’’_D + G₄ + F_i4 + R’_A + R’’_A + G₂ + F_i2 + R_E= 0 (1.3.13).

 

В этом уравнении известны все составляющие по модулю и по направлению кроме R’’_Dи R’’_A (они известны только по направлению). Для их нахождения необходимо построить силовой многоугольник, откладывая последовательно векторы сил.

Вычисляем масштабный коэффициент:

μ_F = R’_D/ P_F R’_D (1.3.14),

μ_F = 0,1/ 2,5 = 0,04 Н/мм

Далее к вектору R’_D достраиваем другие составляющие уравнения (1.3.13), рассчитывая длину векторов при помощи масштабного коэффициента. Находим неизвестные силы R’’_Dи R"_A, зная их направление. Определив их численное значения в мм, переводим это значение в Н с помощью масштабного коэффициента.

R’’_D = m_F· П_F R’’_D = 0,04 · 140 = 5,6 H (1.3.15),

 

где, П_F R’’_D - положение R’’_Dна плане сил.

 

R"_A = m_F· П_F R"_A = 0,04 · 35 = 1,4 H (1.3.16),

 

где, П_F R"_A - положение R"_A на плане сил.

Найдем R_D- результирующую силу в паре D, соединив начало R’_Dи конец R"_D.

Определив его численное значения в мм, переводим это значение в Н с помощью масштабного коэффициента.

R_D = m_F· П_F R_D = 0,04 · 141= 5,64 H (1.3.17),

 

где, П_F R_D - положение R_D на плане сил.

Аналогично найдем R_А - результирующую силу в паре АС, соединив начало R’_А и конец R"_А.

Определив его численное значения в мм, переводим это значение в Н с помощью масштабного коэффициента.

R_A = m_F· П_F R_A = 0,04 · 60 = 2, 4 H (1.3.18),

 

где, П_F R_A - положение R_A на плане сил.

Теперь определим уравновешивающую силу и уравновешивающий момент, действующий на кривошип АВ.

На кривошип АВ действует шатун силой R_A. Считается, что сила F_ур приложена перпендикулярно звену АВ. В этом случае уравнение моментов всех сил, приложенных к кривошипу относительно точки В, имеет вид:

∑М_В = 0

∑М_В = R_A· h₈ + F_ур · l_AB+ G₁ · h₉ = 0 (1.3.19)

F_ур= G₁ · h₉ + R_A · h₈ / l_AB = 0,03 · 0,007 + 2,4 · 0,008 / 0,034 = 0,57 H

M_ур = F_ур· l_AB (1.3.20)

M_ур = 0,57 · 0,034 = 0,02 H · м

Найденные при силовом анализе механизма величины представлены в таблице 1.4.

Таблица 1.4

RE = 1,7 H	RA = 2,4 H	RD = 5,64 H	Fур= 0,57 H
R’E = 0,1 H	R’A = 1,9 H	R’D = 0,1 H	Mур = 0,02 Н · м
R’’E = 1,68 H	R’’A = 1,4 H	R’’D = 5,6 H