Навигация
Наближення Ейнштейна і Дебая
38116
знаков
2
таблицы
12
изображений
1.2 Наближення Ейнштейна і Дебая
В основу першої квантової теорії твердих тіл покладено модель Ейнштейна (1907 p.). Згідно з нею атом кристала являє собою тривимірний гармонічний осцилятор, що виконує коливання з частотою ωЕ поблизу положення рівноваги незалежно від інших атомів. Згідно з цією моделлю, тверде тіло слід розглядати як сукупність 3N квантових осциляторів, що мають однакову частоту. Середня енергія кожного осцилятора визначається за формулою (1.5).
З рис. 1.1 видно, що частоти оптичних коливань кристалічної решітки мало залежать від хвильового вектора 
. Це означає, що до них можна застосувати модель Ейнштейна. За частоту коливань ωЕ осциляторів беруть ω3, яка дорівнює граничному значенню частоти оптичної вітки коливань (рис. 1.1). В моделі твердого тіла Ейнштейна енергію кристала, який містить N атомів, записують так:
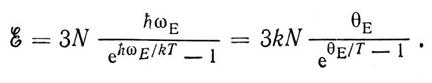(1.6)
У виразі (1.6) введено температуру Ейнштейна
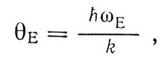
(1.7)
що відповідає збудженню фононів частоти ωf, кількість яких експоненціально зменшується із зниженням температури.
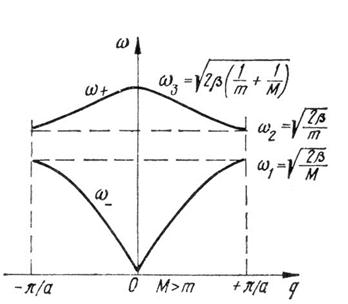
Рис. 1.1
В моделі твердого тіла Ейнштейна вважається, що кожен атом коливається незалежно від інших. Щоб врахувати зв'язок між сусідніми атомами, П. Дебай (1912 р.) розглянув тверде тіло як суцільне пружне середовище. В такій моделі внутрішня енергія твердого тіла пов'язується не з коливаннями окремих атомів, а з стоячими пружними хвилями (модами). Квант коливальної енергії твердого тіла (фонон) переміщується з швидкістю звуку, оскільки власне звукові хвилі пружні. З рис. 1.1 видно, що для всіх значень хвильового числа q ωак < ωоп, Де ωак — частоти акустичних коливань, що відповідають нижній вітці (раніше позначали ω_), а ωоп — частоти оптичних коливань раніше позначали (ω+). Енергетично це означає, що при досить низьких температурах у кристалі збуджені одні тільки акустичні коливання. Через велике число атомів спектр цих коливань можна вважати практично неперервним і таким, що змінюється від ω = 0 до ω1 (рис. 1.1).
Якщо ввести характеристичну температуру (температура Дебая)
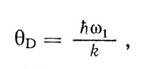
(1.8)
то при Т ≤ θd вкладом оптичних коливань в енергію кристала можна знехтувати.
Для деяких твердих тіл значення θd наведено в табл. 1.1.
Рівноважне число акустичних фононів з енергією ħω в комірці фазового простору об'ємом (2πħ)3 визначають зa формулою (1.4); число комірок фазового простору, що припадає на інтервал,
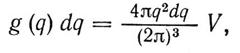
(1.9)
де V — об'єм кристала. Під фазовим простором системи розуміють 6N-вимірний простір узагальнених координат і узагальнених імпульсів системи.
Якщо вважати дисперсію акустичних частот, згідно з (1.8), лінійною функцією q і замінити три акустичні вітки коливань однією (що еквівалентно припущенню, за яким швидкість поширення трьох акустичних хвиль однакова), то (1.9) можна звести до вигляду
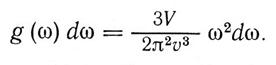(1.10)
Тут множник 3 відповідає трьом акустичним модам (одній поздовжній і двом поперечним), а v — середня швидкість поширення звуку.
Таблиця 1.1
Температури плавлення, Дебая, Фермі і теплоємність
деяких твердих тіл
| Кристал | Густина 1), 103кг/м3 | Тпл | θD, К | θF, К | Ср, Дж/ (моль•К) |
| Ne | 1,503 (10 К) | 25,4 | 63 | — | 20,79 |
| Ar | 1,656 (40 К) | 83,9 | 85 | — | 20,79 |
| C (алмаз) | 3,516 | сублімується | 1860 | — | 6,12 |
| Ge | 5,324 | 1231 | 366 | — | 23,4 |
| Na | 0,966 | 370,9 | 150 | — | 28,12 |
| K | 0,862 | 336,3 | 10 | — | 29,51 |
| Cu | 8,933 | 1356 | 344,4 | 8,12•104 | 24,47 |
| Au | 19,281 | 1336 | 161,6 | 6,39•104 | 25,38 |
| NaCl | 2,167 | 1074 | 321,9 | — | 50,79 |
| KBr | 2,75 | 1003 | 152,8 | — | 51,51 |
1) Дані для 293 К
Вираз (1.10) можна спростити, якщо врахувати умову, що загальне число коливань в трьох акустичних вітках дорівнює 3N, тобто числу ступенів вільності кристала, що містить N атомів: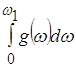 
= 3N. Звідси максимальна частота, що обмежує спектр нормальних акустичних коливань,
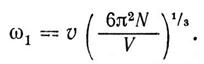
(1.11)
З урахуванням (1.4), (1.10) і (1.11) загальне число фононів в об'ємі V кристала і в інтервалі [ω, ω + dω] (що містить N атомів)
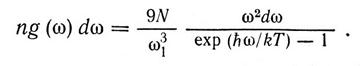
Відповідно повна енергія акустичних фононів в об'ємі
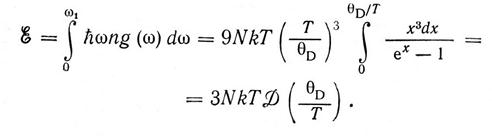
(1.12)
При одержанні (1.12) використано вираз (1.8) для температури Дебая, покладено х = ħω/kТ і введено функцію Дебая
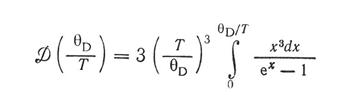
(1.13)
При високих температурах суттєвим стає вплив оптичних коливань на значення фононної енергії кристала.
Похожие работы
... ів на установці ЭМР-100 у режимі дифракції на відображення з поверхні тертя при напрузі, яка з ковзає , 100 кв. 2.3 Математична модель процесів тертя й зношування покрити по пружно - пластичній основі На підставі [12-21] простір існування властивостей детонаційно-газових покриттів можна описати, як: Ω (Rфм Rмф Rфт Rі) З обліком першого обмеження: Ω Ψ де Ψ - простір ...
... класах проходить по-різному. Необхідна її адаптація до конкретних умов проведення [20]. РОЗДІЛ 3. МЕТОДИЧНІ ЗАБЕЗПЕЧЕННЯ ПРОВЕДЕННЯ УРОКІВ З ТЕМИ „МЕТАЛИ” 3.1 Тематичне планування теми „Метали” Тема „Метали” вивчається в 9 класі в середині другого семестру навчального року, на вивчення теми передбачено програмою 22 години. Тематичне планування представлено в табл. 3.1. Таблиця ...
... сполуки”, а також зорієнтовані на їх загальний розвиток. Об’єкт дослідження: процес вивчення теми “Залізо та його сполуки” у класах з поглибленим вивченням хімії,мтворчо та інтелектуально обдарованими учнями. Предмет дослідження: навчання особливості організації та змісту урочної навчальної діяльності учнів. Дане педагогічне дослідження має переваги над існуючою традиційною технологією, яка ...
... ", з’ясовано, що у процесі вивчення молодшими школярами рослин необхідно проводити досліди, спостереження, практичні роботи. 2.2 Методика вивчення молодшими школярами рослин на уроках природознавства у 3 класі Розробляючи методику вивчення молодшими школярами рослин на уроках природознавства, особливу увагу ми приділяли визначенню цілей уроку, добору змісту, доцільних методів і засобів ...
0 комментариев