Навигация
Метод Гюйе і Крумхансла
38116
знаков
2
таблицы
12
изображений
3.3 Метод Гюйе і Крумхансла
Серед методів, заснованих на використанні рівняння Больцмана для фононів, заслуговує уваги робота Гюйе і Крумхансла по гідродинаміці фононів. Вона є порівняно раннім дослідженням загальних властивостей фононних систем. Передбачається, що розподіл фононів залежить від часу і координат. Зміна розподілу по ширині кристала, а також і уздовж його довжини при постійному температурному градієнті приводить до пуазейльовського протікання, тоді як зміна розподілу з часом дозволяє отримати другий звук, який є хвилевим процесом розповсюдження зміни N.
Розгляд ведеться з використанням операторної форми для рівняння Больцмана, і загальні результати виражаються через оператори зіткнень, причому розрізняються оператори для нормального розсіяння N* і для резистивного розсіяння R*. Вирішення рівняння Больцмана і, отже, виразу для потоку тепла і теплопровідності записуються через цих операторів, тому необхідно тільки виразити останні через швидкості релаксації 
і 
, щоб довести відповіді до числових результатів.
За умови N* > R*, відповідному >> , теплопровідність виходить та ж, що і визначувана другим членом виразу Каллуея; отже, вона співпадає з величиною, знайденою варіаційним методом при переважанні N-процесів. За умови R* > N*, відповідному >> , виходить той же вираз для теплопровідності, що і при простому релаксаційному методі; тут вона також співпадає з першим членом у виразі Каллуея.
Гюйе і Крумхансл приводять вираз, справедливий для всього інтервалу відносних значень і :
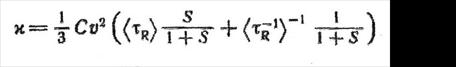
(4.3.1)
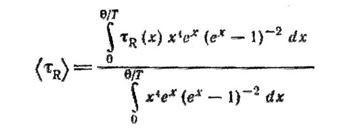
де
а 
– таке ж середнє для [τR(х)]-1. Величина S рівна 
/ 
і називається чинником перемикання. Якщо << , тo величина S велика і в дужках виразу (3.3.1) найбільш важливий член . Peзистивні процеси тоді переважають, і теплопровідність виходить така ж, як при використанні простого релаксаційного методу. У разі τR >> τN величина S мала і головну роль грає член -1. Нормальні процеси визначають розподіли фононів, і вираз для теплопровідності співпадає з формулою Займана і Каллуея для цього граничного випадку, а тепловий опір аддитивний.
У проміжній області відносних значень τR і τN швидкості розсіяння, що отримуються при аналізі експериментів за допомогою виразів Каллуея і Гюйе – Крумхансла, дуже близькі, але погодження дещо гірше, якщо ≈ -1.
висновки
Одним з ефектів, що обумовлений ангармонічним характером коливань атомів, є тепловий опір твердих тіл. Він не міг б виникнути, якби атоми здійснювали строго гармонійні коливання, що розповсюджуються в решітках у вигляді системи пружних хвиль, що не взаємодіють між собою. Відсутність взаємодії між хвилями дозволяла б їм розповсюджуватися в кристалі не розсіваючись, тобто не зустрічаючи ніякого опору, подібно до розповсюдження світла в порожнечі.
Якби в такому кристалі можна було створити різницю температур, то атоми гарячого кінця, що коливаються з великими амплітудами, передавали б свою енергію сусіднім атомам і фронт теплової хвилі розповсюджувався б уздовж кристала із швидкістю звуку. Оскільки ця хвиля не зустрічала б ніякого опору, то навіть при нескінченно малій різниці температур тепловий потік міг би досягати якої завгодно великої величини; теплопровідність такого кристала була б нескінченно великою.
У реальних кристалах при не дуже низьких температурах коливання атомів носять ангармонічний характер. Поява ангармонічності призводить до того, що нормальні коливання решіток втрачають незалежний характер і при зустрічах взаємодіють один з одним, обмінюючись енергією і змінюючи напрям свого розповсюдження (розсіваючись один на одному). Саме внаслідок протікання таких процесів взаємодії пружних хвиль стає можливою передача енергії від коливань однієї частоти до коливань іншої частоти і встановлення в кристалі теплової рівноваги.
Опис процесу розсіяння нормальних коливань один на одному зручно вести на мові фононів, розглядаючи термічно збуджений кристал як ящик, заповнений фононами. У гармонійному наближенні, в якому нормальні коливання решіток є незалежними, фонони утворюють ідеальний газ (газ невзаємодіючих фононів). Перехід до ангармонічних коливань еквівалентний введенню взаємодії між фононами, в результаті якої можуть відбуватися процеси розщеплювання фонона на два і більш і утворення одного фонона з двох. Такі процеси прийнято називати фонон-фононним розсіянням.
Всі процеси розсіяння, внаслідок якого розподіл фононів прагне до рівноважного, прямо впливають на теплопровідність. Для більшості процесів інтенсивність розсіяння залежить від частоти фононів, і N-процеси грають важливу роль, перерозподіляючи енергію між різними модами і тим самим перешкоджаючи сильному відхиленню від рівноважної населеності в кожній моді. Взагалі кажучи, важко виділити внесок від N-процесів, і необхідний досить докладний аналіз експериментальних результатів, щоб зрозуміти, як позначаються N-процеси на теплопровідності. Проте у ряді випадків їх вплив дуже істотний.
список використаної літератури
1. Берман Р. Теплопроводность твердых тел. – М.: Высшая школа, 1979.
2. Бушманов Б.Н., Хромов Ю.А. Физика твердого тела. – Учебн. пособие для втузов. – М.: Высшая школа, 1975. – 224 с.
3. Епифанов Г.И. Физика твердого тела. Учеб. пособие для втузов. – Изд. 2-е, перераб. и доп. – М.: Высшая школа, 1979. – 288 с.
4. Жданов Г.С. Физика твердого тела. – М.: МГУ, 1971.
5. Займан Дж. Принципы теории тевердого тела. – М.: «Мир», 1976.
6. Киттель Ч. Введение в физику твердого тела. – М.: Физматгиз, 1973.
7. Китель Ч. Элементарная физика твердого тела. – М.: «Наука», 1985.
8. Курик М.В., Цмоць В.М. Фізика твердого тіла. – К.: Вища школа. Головне видавництво, 1985. – 246 с.
9. Мартон К., Смит. Основы физики металлов. – М.: Металлургиздат, 1972.
10. Най Дж. Физические свойства кристаллов. – М., ИЛ, 1986.
11. Полежаев Ю.В. Теплопроводность. Физич. словарь. Т. 5. – 1987.
12. Спроул Р. Современная физика. – М.: Физматгиз, 1981.
13. Твердое тело. Структура и свойства. – М.: «Знание», «Физики и физике», 1972.
14. Уэрт Ч., Томсон Р. Физика твердого тела. – М.: «Мир», 1986.
Похожие работы
... ів на установці ЭМР-100 у режимі дифракції на відображення з поверхні тертя при напрузі, яка з ковзає , 100 кв. 2.3 Математична модель процесів тертя й зношування покрити по пружно - пластичній основі На підставі [12-21] простір існування властивостей детонаційно-газових покриттів можна описати, як: Ω (Rфм Rмф Rфт Rі) З обліком першого обмеження: Ω Ψ де Ψ - простір ...
... класах проходить по-різному. Необхідна її адаптація до конкретних умов проведення [20]. РОЗДІЛ 3. МЕТОДИЧНІ ЗАБЕЗПЕЧЕННЯ ПРОВЕДЕННЯ УРОКІВ З ТЕМИ „МЕТАЛИ” 3.1 Тематичне планування теми „Метали” Тема „Метали” вивчається в 9 класі в середині другого семестру навчального року, на вивчення теми передбачено програмою 22 години. Тематичне планування представлено в табл. 3.1. Таблиця ...
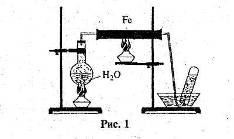
... сполуки”, а також зорієнтовані на їх загальний розвиток. Об’єкт дослідження: процес вивчення теми “Залізо та його сполуки” у класах з поглибленим вивченням хімії,мтворчо та інтелектуально обдарованими учнями. Предмет дослідження: навчання особливості організації та змісту урочної навчальної діяльності учнів. Дане педагогічне дослідження має переваги над існуючою традиційною технологією, яка ...
... ", з’ясовано, що у процесі вивчення молодшими школярами рослин необхідно проводити досліди, спостереження, практичні роботи. 2.2 Методика вивчення молодшими школярами рослин на уроках природознавства у 3 класі Розробляючи методику вивчення молодшими школярами рослин на уроках природознавства, особливу увагу ми приділяли визначенню цілей уроку, добору змісту, доцільних методів і засобів ...
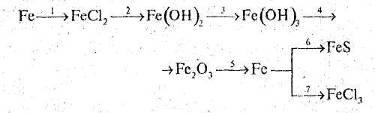
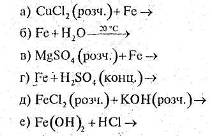
0 комментариев