Навигация
СТАЦИОНАРНАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ
1. СТАЦИОНАРНАЯ ЗАДАЧА ТЕПЛОПРОВОДНОСТИ
Применим уравнение теплопроводности для решения задач, в которых температура зависит только от одной линейной координаты. Примем, что в прямоугольной системе координат температура будет зависеть только от x, а в цилиндрической и сферической системах координат—только от радиуса. Предполагается, что коэффициент теплопроводности является постоянной величиной, а тепловыделение отсутствует.
Применим общую методику решения, состоящую из двух этапов. На первом этапе из решения соответствующего упрощенного уравнения теплопроводности находится распределение температуры. С этой целью отыскивается аналитическое решение дифференциального уравнения второго порядка. После того как решение дифференциального уравнения записано в общем виде, с помощью двух граничных условий определяются две постоянные интегрирования. На втором этапе с помощью закона Фурье вычисляется кондуктивный тепловой поток через твердое тело.
1.1 Общее понятие термического сопротивления
Математическое выражение закона Гука имеет вид:
![]()
или после разделения переменных
![]() ,
,
интегрируя в пределах изменения пространственной координаты и в соответствующем температурном интервале, получаем
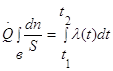 или
или
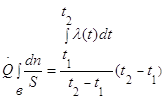
Выражение 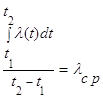
называется среднеинтегральным коэффициентом теплопроводности в интервале ![]() . При линейной зависимости
. При линейной зависимости
![]()
![]()
При постоянном: ![]()
Таким образом, имеем
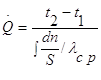
Сравнивая полученное уравнение с выражением закона Ома
![]() ,
,
получаем уравнение, определяющее термическое сопротивление теплопроводности в общем случае
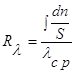 (1.0)
(1.0)
Для получения выражения, определяющего термическое сопротивление конвективного теплообмена, рассмотрим закон Ньютона-Рихмана
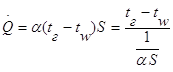
То есть термическое сопротивление конвективного теплообмена определится выражением
![]() (1.01)
(1.01)
1.2 Прямоугольные координаты
Стационарное одномерное распределение температуры в плоской прямоугольной стенке при отсутствии внутреннего тепловыделения описывается упрощенным уравнением теплопроводности
d2T/dx2 = 0.
Решение этого дифференциального уравнения с использованием двух постоянных интегрирования C1 и С2 имеет вид:
Т (х) = С1x + С2.
Значения этих постоянных можно найти, если заданы два граничных условия. Предположим, что в качестве этих условий заданы температуры на двух поверхностях стенки (рисунке 1.1): Т(0)=T1 и T(b)=T2. Применяя эти граничные условия, получаем следующее распределение безразмерной температуры в стенке:
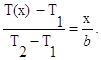 (1.1)
(1.1)
Следовательно, температура изменяется линейно по x. Тепловой поток через стенку определяется законом Фурье:
![]() (1.2)
(1.2)
Тепловой поток на единицу площади называется плотностью теплового потока и обозначается q. Для плоской стенки
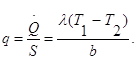
Если записать соотношение (1.2) в форме закона Ома:
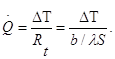 (1.3)
(1.3)
то термическое сопротивление плоской стенки выражается формулой
![]() . (1.4)
. (1.4)
Используя общее понятие термического сопротивления теплопроводности, (1.0), получаем аналогичное выражение
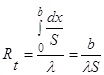
Кондуктивный тепловой поток через плоскую стенку обусловлен перепадом температур поперек стенки, и его распространению противодействует термическое сопротивление, пропорциональное толщине стенки и обратно пропорциональное коэффициенту теплопроводности стенки и площади ее поперечного сечения.
Если кондуктивный перенос тепла осуществляется через составную (многослойную) плоскую стенку, распределение температуры и тепловой поток можно найти, предполагая, что тепло течет по эквивалентной тепловой цепи, представляющей сумму термических сопротивлений, соответствующих отдельным слоям из различных материалов.
В качестве примера тепловой цепи рассмотрим плоскую стенку (индекс 1), покрытую двумя слоями различных изоляционных материалов (индексы 2 и 3). Геометрия задачи показана на рисунке 1.2. Один и тот же тепловой поток проходит последовательно через каждое термическое сопротивление, и, следовательно, тепловая цепь состоит из последовательно соединенных термических сопротивлений. Если известны свойства всех трех материалов, заданы геометрические характеристики и температуры на двух внешних поверхностях, тепловой поток можно найти с помощью соотношения, аналогичного закону Ома:
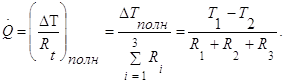 (1.5)
(1.5)
Поскольку тепловой поток через многослойную стенку известен, можно найти температуры на поверхностях раздела материалов, применяя закон Ома для каждого слоя. Например, температуру Тx на поверхности раздела материалов 1 и 2 можно рассчитать по формуле
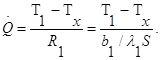 (1.6)
(1.6)
Часто в многослойных стенках слои материалов расположены так, что тепловой поток через них течет скорее параллельно, чем последовательно. В таком случае в тепловую цепь включаются участки из параллельно соединенных термических сопротивлений.
Тепловой поток определяется по формуле
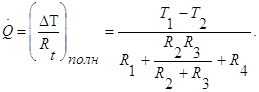 (1.7)
(1.7)
Отдельные термические сопротивления выражаются соотношением
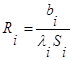 .
. ![]()
Промежуточные температуры типа ТX можно найти из уравнения (1.6).
Предполагается, что при параллельном соединении термических сопротивлений R2 и R3 тепловой поток остается одномерным; если же сопротивления R2 и R3 заметно отличаются друг от друга, могут стать существенными двумерные эффекты.
Похожие работы
... івник стає одним з основних теплосприймальних елементів котельного агрегату. Для виготовлення труб-пакетів пароперегрівника, що працюють у дуже важких температурних умовах, застосовуються дорогі леговані сталі. За видом теплообміну пароперегрівники поділяються на конвективні, напіврадіаційні і радіаційні; за розміщенням змійовиків – на вертикальні і горизонтальні. У старих конструкціях котлів ...
... на велику витрату металу на зовнішні труби, що не беруть участь в теплообміні; - трудність очищення міжтрубного простору. 2. Місце і призначення проектованого апарата в технологічній схемі Теплообмінник типу «труба в трубі» використовується в процесі згущення продуктів, що є підготовчим етапом перед висушуванням бульйону. Процес згущення протікає наступним чином: Бульйон всмоктується у вирі ...
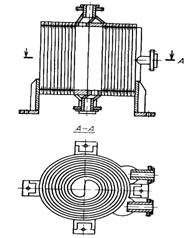
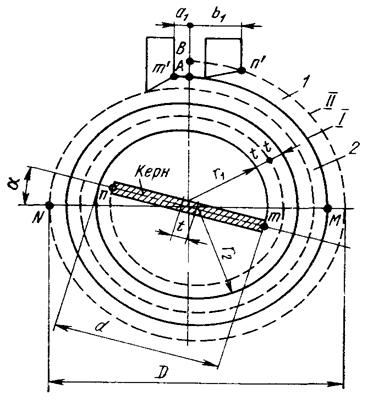
... , Х17Н12М2Т. Для виготовлення кришок застосовується двошарові сталі Ст3+10Х18Н10Т та 20К+Х17Н13М2Т та ін. Для виготовлення прокладок застосовують гуму, пароніт, фторопласт, азбестовий картон та ін. Спіральні теплообмінні апарати для рідини складаються із корпуса з тупиковими каналами, двох плоских кришок по торцям із прокладками, чотирьох штуцерів для введення та виведення теплообмінювальних ...
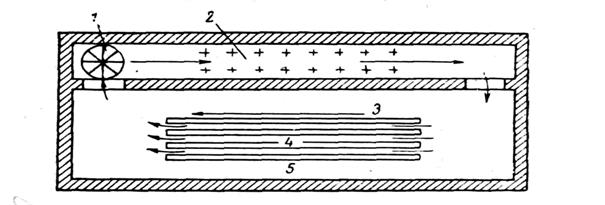
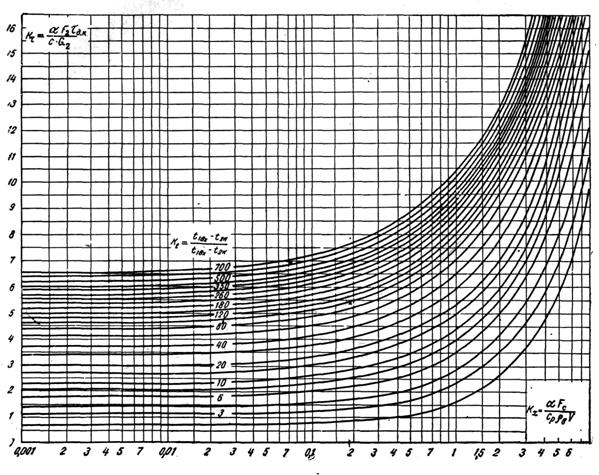
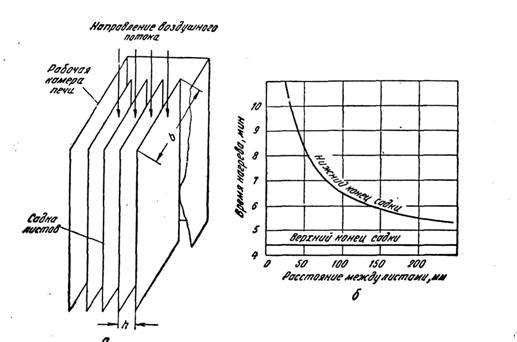
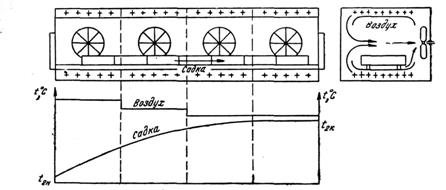
... ее установленную мощность: (37) Рассчитав по формуле (37) количество изделий, необходимо сравнить получающуюся при этом продолжительность нагрева изделий [по формуле (35)] с допустимой по технологии. 3. Особенности нагрева длинномерных изделий в электрических конвекционных печах периодического действия Большое количество различных длинномерных полуфабрикатов (профили, трубы, листы и т. ...

0 комментариев