Навигация
Цилиндрические координаты
1.3 Цилиндрические координаты
Из задач теплопроводности для тел цилиндрической формы чаще всего встречается задача о кондуктивном тепловом потоке через длинный полый цилиндр (рисунок 1.3). Известно, что температура внутренней поверхности цилиндра равна Ti, а температура наружной поверхности То. Стационарное распределение температуры в твердом теле с постоянными теплофизическими свойствами при отсутствии внутреннего тепловыделения определяется решением уравнения теплопроводности при двух граничных условиях: Т(ri)=Ti; Т(r0)=Т0. Решение для местной температуры Т(r) имеет вид
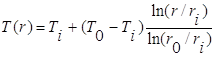 (1.8)
(1.8)
Выражение (1.8) записывается в безразмерной форме следующим образом:
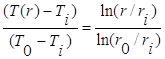 . (1.9)
. (1.9)
Следовательно, температура изменяется в радиальном направлении по логарифмическому закону.
Поскольку распределение температуры известно, тепловой поток вдоль радиуса цилиндра можно найти с помощью закона Фурье для цилиндрической системы координат,
![]() (1.10)
(1.10)
где ![]() — длина цилиндра.
— длина цилиндра.
Дифференцируя распределение температуры (1.8) и подставляя полученный результат в соотношение (1.10), получаем
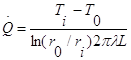 (1.11)
(1.11)
Выражение (1.11) записано в форме закона Ома, и знаменатель представляет собой термическое сопротивление полого цилиндра:
![]() (1.12)
(1.12)
Используем интегральную форму представленного термического сопротивления. Получаем
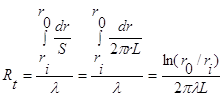
Принципы последовательного и параллельного соединения термических сопротивлений в цепь, справедливые для плоской стенки в прямоугольной системе координат, можно применить и для задачи о теплопроводности в полом цилиндре. Предположим, например, что жидкость течет в трубе, покрытой теплоизоляционным материалом (рисунок 1.4). Известно, что средняя температура жидкости равна T1, а температура внешней поверхности изоляции Т2. Характеристики материала трубы обозначены индексом 1, а изоляции—индексом 2. Конвективное термическое сопротивление жидкости определяется формулой (1.01). Конвективное термическое сопротивление жидкости нужно соединить последовательно с двумя кондуктивными термическими сопротивлениями для двух твердых материалов, поскольку тепловой поток распространяется последовательно через каждый из этих материалов.
Тепловой поток в этой задаче выражается соотношением:
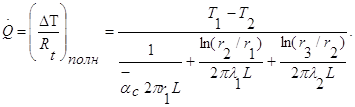 (1.13)
(1.13)
Термическое сопротивление, входящее в соотношение (1.13), является суммой всех термических сопротивлений между двумя известными температурами. Если известны температуры Т1и Т2, то полное сопротивление должно равняться сумме только кондуктивных сопротивлений трубы и изоляции. Температура Тx при известном тепловом потоке находится из соотношения
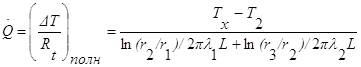 (1.14)
(1.14)
1.4 Сферические координаты
Распределение температуры и тепловой поток для полого шара определяются таким же образом, как для полого цилиндра и плоской стенки. Стационарное одномерное распределение температуры при отсутствии внутреннего тепловыделения определяется из решения упрощенного уравнения теплопроводности, записанного в сферических координатах. Это уравнение имеет вид
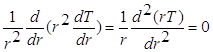
Предполагаем, что граничными условиями являются заданные температуры внутренней и наружной поверхности шара (рисунок 1.5.): Т(ri)=Ti; Т(r0)=Т0. В таком случае распределение температуры в полом шаре определяется соотношением
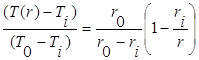 (1.15)
(1.15)
Следовательно, температура полого шара изменяется в радиальном направлении по гиперболическому закону.
Тепловой поток через стенку шара можно найти, применяя закон Фурье к соотношению (1.15). В итоге получаем
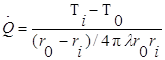 (1.16)
(1.16)
Таким образом, термическое сопротивление стенки шара выражается формулой
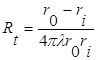 (1.17)
(1.17)
Для интегрального представления ![]() имеем
имеем
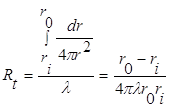
Использование интегрального представления ![]() более универсально, не требует математического описания, интегрирования дифференциального уравнения, определения констант и т. д.
более универсально, не требует математического описания, интегрирования дифференциального уравнения, определения констант и т. д.
Похожие работы
... івник стає одним з основних теплосприймальних елементів котельного агрегату. Для виготовлення труб-пакетів пароперегрівника, що працюють у дуже важких температурних умовах, застосовуються дорогі леговані сталі. За видом теплообміну пароперегрівники поділяються на конвективні, напіврадіаційні і радіаційні; за розміщенням змійовиків – на вертикальні і горизонтальні. У старих конструкціях котлів ...
... на велику витрату металу на зовнішні труби, що не беруть участь в теплообміні; - трудність очищення міжтрубного простору. 2. Місце і призначення проектованого апарата в технологічній схемі Теплообмінник типу «труба в трубі» використовується в процесі згущення продуктів, що є підготовчим етапом перед висушуванням бульйону. Процес згущення протікає наступним чином: Бульйон всмоктується у вирі ...
... , Х17Н12М2Т. Для виготовлення кришок застосовується двошарові сталі Ст3+10Х18Н10Т та 20К+Х17Н13М2Т та ін. Для виготовлення прокладок застосовують гуму, пароніт, фторопласт, азбестовий картон та ін. Спіральні теплообмінні апарати для рідини складаються із корпуса з тупиковими каналами, двох плоских кришок по торцям із прокладками, чотирьох штуцерів для введення та виведення теплообмінювальних ...
... ее установленную мощность: (37) Рассчитав по формуле (37) количество изделий, необходимо сравнить получающуюся при этом продолжительность нагрева изделий [по формуле (35)] с допустимой по технологии. 3. Особенности нагрева длинномерных изделий в электрических конвекционных печах периодического действия Большое количество различных длинномерных полуфабрикатов (профили, трубы, листы и т. ...
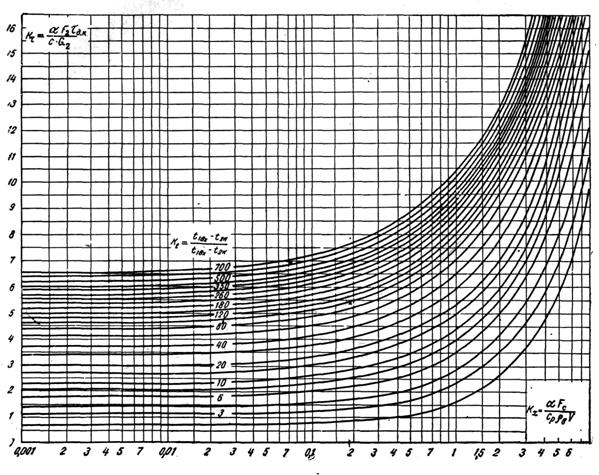
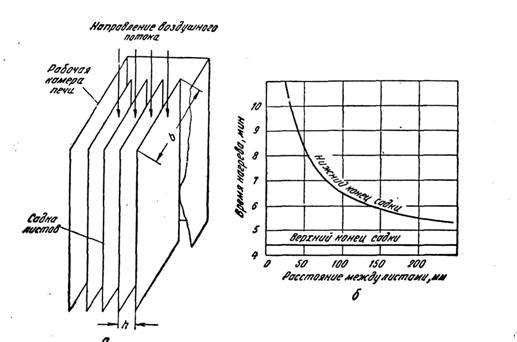

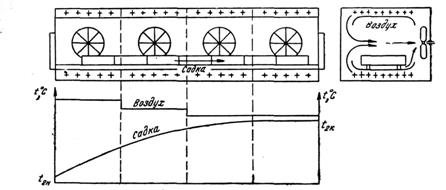
0 комментариев