Навигация
Вероятности, энтропия и энергия. Канонический ансамбль Гиббса
Микросостояния в ансамбле для удобства пронумеруем множеством {…, a, a+1,…i,…}. Построить необходимые математические соотношения, описывающие свойства канонического ансамбля Гиббса, можно проще всего, исходя из хорошо известных формул классической феноменологической термодинамики.
КАНОНИЧЕСКИЙ АНСАМБЛЬ образован из состояний равновесной изохорно-изотермической системы (V,T=const).
Каждое микросостояние совместимо с наблюдаемым макросостоянием коллектива, и это означает, что все они характеризуются одним и тем же значением наблюдаемых макроскопических параметров и свободной энергии A, т.е.:
![]() ; (1)
; (1)
В разных микросостояниях энтропия и внутренняя энергия (Ui; Si) системы могут различаться, но неизменна их свободная энергия. Справедлива цепочка равенств:
![]() ; (2)
; (2)
Энтропия S статистического коллектива и термодинамическая вероятность W связаны законом Больцмана-Планка: ![]() ; (3)
; (3)
Отсюда возникает цепочка равенств:
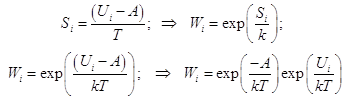 (4)
(4)
Термодинамическая вероятность W макросостояния коллектива это число всех приводящих к нему комбинаций всех элементов между их возможными микросостояниями.
Каждая из комбинаций и порождает отдельное микросостояние колектива.
Поэтому всегда W>1. Очевидно минимум W =1 имеет место лишь в предельном случае идеально упорядоченного состояния коллектива (на атомно-молекулярном уровне – это состояния идеального кристалла), а во всех прочих случаях она больше единицы W>1.
Важны некоторые простые и почти очевидные соображения.
1. Вероятности и статистические суммы.
Математическая вероятность w каждого из микросостояний, входящих в макросостояние, это его доля во всём ансамбле, т.е. доля в макросостоянии. Она обратна термодинамической вероятности w =1/W и меньше единицы w <1.
Математические вероятности можно нормировать:
![]() (1.1)
(1.1)
Всем микросостояниям отвечает одинаковая свободная энергия A, и поэтому множитель с нею можно вынести за знак суммы:
![]() (1.2)
(1.2)
Второй сомножитель содержит сумму всех факторов Гиббса. Его называют суммой состояний, или суммой по состояниям, или статистической суммой исследуемого статистического коллектива (термодинамической системы) и обозначают как
![]() (1.3)
(1.3)
Получаются очевидные соотношения,
![]() ; (1.4)
; (1.4)
Вероятность микросостояния это одно из слагаемых суммы, и его можно выделить ![]() ; (1.5)
; (1.5)
Часто применяется форма канонического распределения:
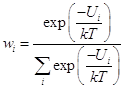 ; (1.6)
; (1.6)
2. Каноническое распределение по состояниям.
Запишем основную формулу:
![]() (2.1)
(2.1)
Если у нескольких микросостояний энергии равны, то они относятся к общему вырожденному энергетическому уровню, а их вероятности одинаковы.
В этом случае удобно ввести кратности вырождения уровней gi. Объединяя равные слагаемые в формуле, статистическую сумму выражают через уровни:
![]() ; (2.2)
; (2.2)
Получают распределение по уровням.
Оно очень удобно для анализа квантовых стационарных движений.
3. Невзаимодействующие подсистемы.
Если части системы (A,B,… K,…) не взаимодействуют между собою, то энергия системы аддитивна и является просто суммой энергий подсистем
![]() ; (3.1)
; (3.1)
Энергию можно суммировать двояко. Можно найти суммарные энергии всех движений одной частицы, затем уже суммируя энергии частиц. Можно также суммировать энергию одного вида у всех частиц в коллективе, а уже затем суммировать коллективные энергии отдельных движений. Так в качестве подсистем могут оказаться как частицы, так и виды движений.
Статистическая сумма системы это мультипликативная функция. Она является произведением статистических сумм подсистем, составляющих систему. Чтобы убедиться в этом, обозначим подсистемы [A,B, …].
Энергетический уровень всей системы это сумма уровней невзаимодействующих подсистем. Если энергии суть EA, EB, то у системы уже EAB=EA+EB.
Если вырожденности (статистические веса) двух подсистем A, B равны gA, gB, то у системы AB это уже gAB=gAgB.
Образуем распределение Гиббса для системы из двух подсистем. Соответственно
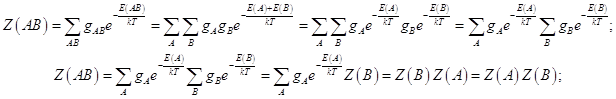 (13.2)
(13.2)
Cтатистическая сумма системы обладает свойством мультипликативности: её сомножители это статистические суммы её подсистем.
Статистический подход оперирует исключительно энергетическими уровнями и состояниями в разных комбинациях.
Поэтому в качестве подсистем могут рассматриваться и материальные части коллектива, и отдельные виды движения, у которых можно выделить самостоятельные наборы квантовых состояний.
Похожие работы
... необходимые термодинамические характеристики, а именно: (3.1) Построить явный вид функции свободной энергии для некоторых относительно простых систем можно методом статистической термодинамики. 4. О равновесии. В любом естественно протекающем (самопроизвольном или свободном) процессе свободная энергия системы понижается. При достижении системой состояния термодинамического равновесия её ...
... и выдвигает новое определение: все системы, допускающие несводимое вероятностное описание, по определению считаются хаотическими [1, с.9]. 3. БРЮССЕЛЬСКАЯ ИНТЕРПРЕТАЦИЯ КВАНТОВОЙ МЕХАНИКИ Э.Шрёдингер 3.1 Альтернативные интерпретации квантовой механики Вероятно, квантовая механика – одна из немногих, если не единственная работающая физическая теория, по поводу интерпретации которой ...
... 1292/(2.016´256)] 3/2´ [43.12/(4.597´7430)] ´(2´2/12) =0.031´18.136´4=183.1´0.0544´4=39.84. Колебательные статистические суммы [q0(HI)] –2 @ 1. [q0(H2)] @1. [q0(I2)] =2.80. Электронный сомножитель: exp(-DU0o/RT) = exp(1.676) = 5.348 Константа равновесия равна: K=5.348´39.84/2.80=76.1. Резюме: Простота приближений и пренебрежение ...
... , что именно такая форма и должна возникать, нет. Давайте теперь сделаем передышку и поймем, что же мы получили. Мы (а точнее, Тсаллис) придумали некоторое обобщение термодинамического подхода. Действительно, обычная термодинамика получается из нашего общего подхода при вполне конкретном значении параметра q = 1. Если же q отлично от 1, то мы имеем уже иную теорию, со своими законами, которые нам ...

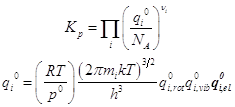
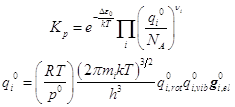
0 комментариев