Навигация
Статистические суммы и свободные энергии у невзаимодействующих подсистем
9814
знаков
0
таблиц
2
изображения
3.1. Статистические суммы и свободные энергии у невзаимодействующих подсистем.
Так, если статистическая сумма одной частицы равна Q, то для коллектива из N частиц сумма состояний в силу мультипликативности примет вид
;
Более просто это выражение запишется как
. (3.3)
Так же обстоит дело и для различных видов движения. Если каждому отдельному виду движения в системе отвечает своя сумма состояний, то результирующая сумма для совокупности движений есть их произведение.
Например, обозначая статистические суммы одиночной молекулы отдельно для поступательного(t-translation), вращательного(r-rotation), колебательного(V-vibration), электронного(e-electronic), ядерного (n-nuclear) движений (стационарных состояний) в виде qt, qr, qV, qe, qn, следует записать молекулярную сумму Q в виде их произведения
Q trVen =qt× qr× qV × qe× qn; (3.4)
Из-за мультипликативности суммы состояния свободная энергия оказывается аддитивной величиной. Её можно суммировать как по отдельным частицам коллектива, так и по видам движения. Соответственно, свободные энергии частицы и коллектива имеют вид
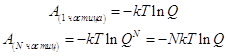; (3.5)
Так же и виды движения в коллективе проявляются в свойствах коллектива.
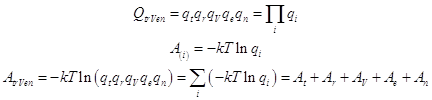; (3.6)
Суммы состояний и свободные энергии с такими простыми свойствами дают очень хорошее начальное приближение для исследования реального коллектива, в котором важна роль взаимодействий между его элементами – статистическими подсистемами.
4. Каноническое распределение по уровням.
Набором квантовых состояний – уровней определяется любого коллектива целиком определяется его полная статистическая сумма состояний и его свободная энергия
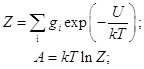(4.1)
Канонический ансамбль состояний описывает реальную изотермическую систему при постоянной температуре. Коллектив - система может быть макроскопическим, и должен состоять из огромного числа однотипных подсистем.
Если коллектив состоит из микроскопических элементов –атомов и молекул, то в отсутствие взаимодействий между ними получаем модель статистического идеального газа.
Каноническое распределение Гиббса становится распределением Больцмана, а факторы Гиббса превращаются в факторы Больцмана. Статистические свойства идеального газа блестяще описываются даже на основе простейших квантовых моделей молекулярных движений с поправками, посредством которых учитываются свойства симметрии коллектива.
5. Идеальный газ. Распределение Больцмана.
Распределение Больцмана описывает изотермическую систему множества однотипных невзаимодействующих между собою частиц. Поэтому его называют распределением для идеального газа. Это предел распределения Гиббса для коллектива и ансамбля состояний частиц идеального газа.
Для такого случая символ Z полной статистической суммы коллектива заменяется символом Q полной статистической суммы идеального газа.
6. Уровни простейших стационарных движений.
Уровни квантовых систем получают из уравнения Шрёдингера.
6.1) Простейшее поступательное движение. Уровни одномерного ящика.
Поступательные уровни замкнутой системы – «ящика».
; (6.1)
6.2) Простейшее вращательное движение. Ротатор.
Вращательные уровни линейной частицы
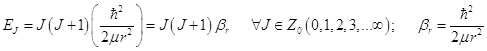; (16.2)
; (16.3)
16.3) Простейшее колебательное движение. Осциллятор (Вибратор).
Колебательные уровни.
; (6.4)
7. Статистические суммы для простейших стационарных движений.
7.1) Поступательная статистическая сумма одномерного движения.
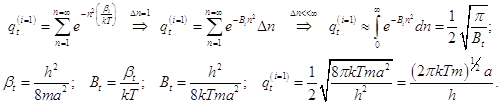(7.1)
Здесь использован стандартный интеграл – интеграл Пуассона 
; (17.2)
ВНИМАНИЕ! Результат предварительный: 
; (7.3)
Полученное выражение необходимо скорректировать и учесть неразличимость частиц вследствие перемешивания газа за счёт броуновского движения.
7.2) Вращательная статистическая сумма линейной молекулы.
Расчёт приближённый – для молекул с достаточно большой массой обоих атомов.
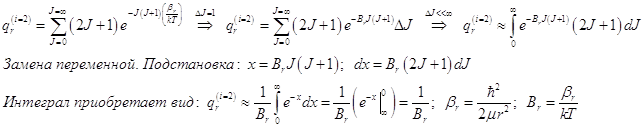(17.4)
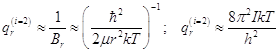
Формула применима для частиц с очень близко расположенными вращательными уровнями. Это имеет место у молекул тяжёлых. Для молекул, содержащих водород и его изотопы эта формула не вполне точна, и статистическая сумма вращения вычисляется численно прямым суммированием.
ВНИМАНИЕ! Результат предварительный: 
; (7.5)
Полученное выражение необходимо скорректировать и учесть неразличимость ориентаций молекулы, возникающих при её самосовмещении при повороте.
7.3) Статистическая сумма для гармонического колебания.
Расчёт проводится от нуля энергии колебания. Квантовое число основного уровня v=1/2 отвечает низшему колебательному уровню
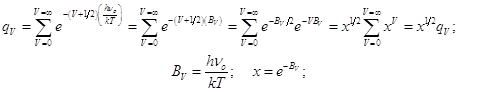; (7.6)
Если 
то сумма представляет собой убывающую геометрическую прогрессию. Это даёт возможность выполнить простые преобразования:
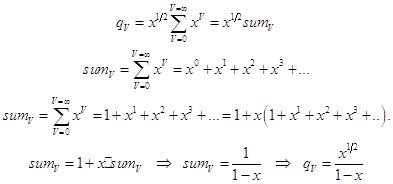; (7.7)
Получено выражение колебательной суммы состояний при отсчёте энергии от запрещённого для осиллятора нулевого значения.
Результат: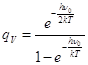 
; (7.8)
18.2) Вибрационная сумма состояний (от E=0) (1 степень свободы).
Формулу (18.1) можно представить равносильным способом.
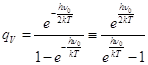; (8.1)
8.3) Вибрационная сумма состояний (от основного уровня V=1/2, E=hn0/2).
При отсчёте энергии уровней от минимально допустимого значения (от уровня с колебательным квантовым числом V=1/2) статистическая сумма (7.8 или 8.1) упрощается, принимая вид (8.2). Это удобнее для практических вычислений, поскольку энергия колебаний отсчитывается уже непосредственно от уровня основного электронно-колебательного состояния - D, от которого определяется энергия диссоциации молекулы или соответствующей химической связи на нейтральные атомы. Такая диссоциация требует меньших затрат, но возможен распад связи и на заряженные ионы. Для этого необходимы дополнительные затраты энергии на преодолению сил кулоновского притяжения ионов, а энергия диссоциации на ионы возрастает.
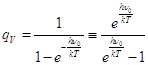; (8.2)
Похожие работы
... необходимые термодинамические характеристики, а именно: (3.1) Построить явный вид функции свободной энергии для некоторых относительно простых систем можно методом статистической термодинамики. 4. О равновесии. В любом естественно протекающем (самопроизвольном или свободном) процессе свободная энергия системы понижается. При достижении системой состояния термодинамического равновесия её ...
... и выдвигает новое определение: все системы, допускающие несводимое вероятностное описание, по определению считаются хаотическими [1, с.9]. 3. БРЮССЕЛЬСКАЯ ИНТЕРПРЕТАЦИЯ КВАНТОВОЙ МЕХАНИКИ Э.Шрёдингер 3.1 Альтернативные интерпретации квантовой механики Вероятно, квантовая механика – одна из немногих, если не единственная работающая физическая теория, по поводу интерпретации которой ...
... 1292/(2.016´256)] 3/2´ [43.12/(4.597´7430)] ´(2´2/12) =0.031´18.136´4=183.1´0.0544´4=39.84. Колебательные статистические суммы [q0(HI)] –2 @ 1. [q0(H2)] @1. [q0(I2)] =2.80. Электронный сомножитель: exp(-DU0o/RT) = exp(1.676) = 5.348 Константа равновесия равна: K=5.348´39.84/2.80=76.1. Резюме: Простота приближений и пренебрежение ...
... , что именно такая форма и должна возникать, нет. Давайте теперь сделаем передышку и поймем, что же мы получили. Мы (а точнее, Тсаллис) придумали некоторое обобщение термодинамического подхода. Действительно, обычная термодинамика получается из нашего общего подхода при вполне конкретном значении параметра q = 1. Если же q отлично от 1, то мы имеем уже иную теорию, со своими законами, которые нам ...
0 комментариев