Навигация
Алгоритми і методи обчислення
Херсонський національний технічний університет
Контрольна робота
з дисципліни:
«Алгоритми і методи обчислення»Виконала
студентка групи 2зКСМ2
Петрова К.В
Перевірив
Костін В.О
Херсон – 20061. Етапи розв'язування інженерних задач на ЕОМ 1.1 Математика й реальність
Розповсюджений погляд, що математика - це специфічна мова. Ця думка має певне підґрунтя. Математика має усі ознаки мови. У зв‘язку з цим постають деякі практичні питання, пов‘язані із застосуванням математики у житті.
Завдяки певним рисам сучасного викладання математики у школі, іноді частина випускників сприймає математику як зібрання (зведення) деякої кількості правил, які мають до дійсності досить мале відношення, а у головному вигадані людьми - математиками. Це уявлення може бути досить стійким і підтримується в учнях завдяки тому, що головне наполягання у викладанні математиці здійснюється часто-густо не на задачі з життя, а на виконання математичних вправ, в яких головне - не відкрити для себе щось нове у оточуючому житті, а міцно закріпити математичні правила оперування з математичними об'єктами. Це те саме, що при вивченні мови замість опанування змістом нових слів, вивчати лише правила граматичного поєднання слів у речення. Таке уявлення про математику глибоко хибне й шкідливе. Варто нагадати, що саме завдяки досягненням математики, людство спромоглося піднятися на сучасний рівень цивілізації.
Зазначимо, що будь-яка мова складається не лише із правил побудови слів та речень. Найважливішою складовою кожної мови є її змістовна частина, тобто ділянка реальної дійсності, що описується за допомогою цієї мови. Без такої ділянки немає і самої мови. Без установлення змістовного зв'язку між словами мови й об'єктами дійсності, які вони позначають, немає сенсу і вести мову про мову. Власне мову і призначено задля відображення частини реальної дійсності, зберігання й передавання інформації про неї.
У математиці як мові є також ділянка дійсності, про яку математика говорить. Наприклад, арифметика розмовляє з нами про деякі однорідні речі (предмети), надаючи можливість висновувати про їхні кількісні відношення і про їхнє змінювання при реальному оперуванні цими речами.
Коли ми пишемо ![]() , то розуміємо, що маємо купу з
, то розуміємо, що маємо купу з ![]() однакових предметів і іншу купу з
однакових предметів і іншу купу з ![]() таких предметів і додаємо предмети з другої купи до першої. При цьому неявно припускається, що кожна річ із кожної купи існує окремо, незалежно від інших, має деяку стабільність (не змінюється з часом), займає деяку ділянку простору, може переміщуватися у просторі, не змінюючись, може приєднуватися до інших предметів, не змішуючись із ними. І всі ці особливості не вигадані, вони взяті зі спостережень за реальними речами, наприклад, за стадами тварин тощо. Саме із реальної дійсності узята й сама операція додавання, яка математично узагальнює реальні дії по переміщенню окремих речей з одного місця у друге, де вже розміщено інші аналогічні речі. Саме із практики, завдяки простому перераховуванню, було встановлено, що 2+2=4. Подібна операція зворотного напрямку (коли з купи речей відбираються окремі речі і переносяться у інше місце) була названа у математиці відніманням. А через те, що практично усі математичні дії походять з операції додавання як головної, то можна висновувати, що уся математика спирається саме на описані властивості речей і дій з ними.
таких предметів і додаємо предмети з другої купи до першої. При цьому неявно припускається, що кожна річ із кожної купи існує окремо, незалежно від інших, має деяку стабільність (не змінюється з часом), займає деяку ділянку простору, може переміщуватися у просторі, не змінюючись, може приєднуватися до інших предметів, не змішуючись із ними. І всі ці особливості не вигадані, вони взяті зі спостережень за реальними речами, наприклад, за стадами тварин тощо. Саме із реальної дійсності узята й сама операція додавання, яка математично узагальнює реальні дії по переміщенню окремих речей з одного місця у друге, де вже розміщено інші аналогічні речі. Саме із практики, завдяки простому перераховуванню, було встановлено, що 2+2=4. Подібна операція зворотного напрямку (коли з купи речей відбираються окремі речі і переносяться у інше місце) була названа у математиці відніманням. А через те, що практично усі математичні дії походять з операції додавання як головної, то можна висновувати, що уся математика спирається саме на описані властивості речей і дій з ними.
Таким чином, практично усі властивості математичних об'єктів узяті з реальної дійсності і лише дещо узагальнені. При цьому варто дати собі раду у тому, що математичні дії й оператори мають відношення зовсім не до будь-якої сфери дійсності, а лише до таких її частин, які мають вищезазначені властивості.
Перш за все до таких властивостей відноситься існування реальної операції додавання, яка має таки властивості:
n асоціативності: ![]() ; ця властивість (результат рахунку не залежить від того, у якому порядку здійснюється додавання) має належати реальній операції додавання речей, які переліковуються;
; ця властивість (результат рахунку не залежить від того, у якому порядку здійснюється додавання) має належати реальній операції додавання речей, які переліковуються;
n комутативності: ![]() ; результат додавання не залежить від того, до якої купи додаються речі з інших куп; ця властивість теж не є вигаданою, вона має належати реальній операції додавання речей;
; результат додавання не залежить від того, до якої купи додаються речі з інших куп; ця властивість теж не є вигаданою, вона має належати реальній операції додавання речей;
n наявність нуля - є місце, а в ньому немає речей; і ця властивість повинна мати місце у дійсних операціях із речами, що перераховуються;
n операція додавання має приводити до результату, який кількісно перевищує кожний з доданків.
Якщо хоча б одна із зазначених властивостей на практиці не властива фізичній операції додавання, до цих речей не можна прикладати математичні дії. А таких речей безліч у нашому оточенні.
Перш за все до них відносяться так звані якісні величини. Наприклад, важко уявити собі реальні операції з речами, внаслідок якої можна було б додавати одна до одній гладкість, гіркоту, або твердість. Деякі з величин можна деяким чином вимірювати, наприклад, твердість матеріалів, або гладкість поверхонь. Але якщо для них неможливо вказати операції їхнього фізичного додавання, яка б мала усі зазначені властивості, такі кількісні величини називають екстенсивними. До них, наприклад, можна віднести таку фізичну величину, як температура, а також вищевказані твердість і гладкість.
Кількісні (тобто такі, які можуть бути тим чи іншим способом виміряні) величини, для яких установлено реальну (фізичну) операцію додавання, називають інтенсивними. До інтенсивних відносяться більшість фізичних величин. Переміщення, маса тіл, електричний струм, напруга, механічна напруга, сила, моменти сил, час - усе це приклади інтенсивних величин. Деякі з цих величин мають власну фізичну операцію додавання, інші - ні, але можуть бути подані як деякі прості функції від тих величин, що мають таку операцію.
Наприклад, операцією додавання для довжини (або переміщення) є така, коли початок однієї із двох довжин сполучається з кінцем другої. Результатом при цьому вважається довжина від початку другої довжини до кінця першої. Неважко впевнитися, що за умови розташування довжин вдовж однієї прямої в одному напрямку, така операція матиме усі ознаки операції додавання. У випадку просторового переміщення (або довільного розташування довжин у просторі) аналогічна операція є слушною по відношенню до будь-яких трьох ортогональних напрямків. У цілому в результаті одержуємо правило векторного додавання переміщень у просторі.
Для часу операція додавання може виглядати наступним чином: початок другого процесу сполучається з кінцем першого. Результатом є тривалість від початку першого процесу до кінця другого.
Додавання мас збігається з операцією жорсткого з'єднання мас в одну масу.
Додавання електричних зарядів полягає у об'єднанні зарядів при дотиканні заряджених тіл.
Величини, що є похідними від тих, що мають операцію додавання, також є інтенсивними. Наприклад, інтенсивною величиною є швидкість, яка визначається як результат ділення переміщення на проміжок часу, протягом якого це переміщення здійснюється, а також прискорення матеріальної точки. Аналогічно, електричний струм, що визначається як відношення приросту електричного заряду до проміжку часу, за який цей приріст відбувся, також є інтенсивною величиною.
Виходячи з того, що усі математичні операції (віднімання, множення, ділення, піднесення до степеня, взяття похідної та інтегрування) є похідними від операції додавання, можна зробити висновок, що у повній мірі математичні висновки торкаються лише інтенсивних величин. Лише по відношенню до цих величин можна застосовувати усі здобутки математики як мови.
Математика (принаймні, це стосується диференціального й інтегрального зчислень, теорії диференціальних і інтегральних рівнянь) - це мова про інтенсивні величини, тобто, повторимо, про величини, які, з одного боку, є вимірюваними (кількісними), а, з іншого боку, мають реальну фізичну операцію додавання.
1.2 МоделюванняМоделювання є основою пізнання людиною навколишнього світу. Проводячи експерименти, теоретичні досліджування, навіть обговорювання власних дій, намірів, висновків, ми практично займаємось моделюванням. Цілі, задачі, засоби й методи моделювання у цих випадках значно відрізняються один від одного, але загальна спрямованість залишається єдиною - одержання нового знання шляхом випробування (досліджування) деякого замінника реального об'єкта дослідження - моделі. У випадку експериментальних досліджень моделлю є реальний об'єкт, який має ту саму фізичну природу, що й досліджуваний об'єкт. При теоретичних досліджуваннях модель має знакову форму - математичних формул, співвідношень, рівнянь, а задачею моделювання є встановлення нових знань про об'єкти, що описуються цими співвідношеннями. Обговорення встановлює слушність тих припущень і висновків, які були зроблені, шляхом моделювання відношення до них досвідчених співрозмовників.
Узагалі, спрощено, моделювання можна розглядати як певний експеримент, об'єктом якого у першому випадку є матеріальний аналог досліджуваного об'єкта, у другому випадку об'єктом іспитів є знакова (математична) модель, у третьому - відношення до моделі, яка обмірковується, з боку громади.
Результатом розв'язування інженерних (прикладних) задач будь-якого рівня є, як правило, чисельні оцінки (параметрів пристроїв, процесів, технічних і економічних характеристик, тощо), які є наслідком розрахунків, що здійснюються з наближеними первісними даними. Більшість прикладних задач зводяться до математичних задач, які розв'язуються різноманітними обчислювальними методами.
Послідовність розв'язуванні таких задач можна подати у виді наступних етапів:
1) постановка задачі;
2) створення математичної моделі (формулювання задачі); перевірка моделі на адекватність;
3) побудова розрахункової (обчислювальної) моделі, яка відповідає прийнятій математичній моделі;
4) проведення розрахунків за обраною обчислювальною моделлю при заданих (відомих) значеннях первісних даних;
5) аналіз одержаних результатів.
У цілому процес розв'язування інженерної задачі може бути поданий у вигляді схеми, наведеної на рис. 1.1.
Розглянемо докладніше кожний з цих етапів.
| ||||
| ||||
![]()
Похибка ММ
Математична
модель
|
(алгоритм, програма)
|
![]()
початкових даних
![]() Результат
Результат
моделювання
|
Рис. 1.1 Схема розв'язування інженерної задачі
1.3 Постановка задачіПостановка задачі має передумовою словесне, змістовне формулювання задачі, умов, за яких вона ставиться, та вимог до її розв'язування. Слова "змістовне формулювання" слід розуміти так, що задача має бути сформульована у термінах опису реального об'єкта (технічного пристрою або процесу), поводження якого підлягає вивченню.
Як приклади розглядатимемо такі найпростіші інженерні задачі.
Задача 1. Визначити характеристики власного руху фізичного маятника за умови малих його коливань.
Задача 2. Визначити змінення швидкості тіла при його падінні, враховуючи опір оточуючого середовища.
Задача 3. Відшукати моменти інерції ротора гіроскопа.
Задача 4. Визначити характеристики власного руху гіроскопа у кардановому підвісі, а також характеристики його вимушеного руху під дією моментів зовнішніх сил, що діють по осях карданового підвісу і змінюються з часом за гармонічним законом.
1.4 Створення математичної моделіМатематична модель - це математичний опис співвідношень постановки задачі. Такий опис можливий лише на ґрунті попередньо одержаних знань про поводження об'єкта, що вивчається, і про способи правильного й ефективного опису цього поводження у математичних термінах. В одних випадках утворення математичної моделі не складає труднощів (наприклад, модель є відомою заздалегідь за результатами раніше проведених досліджень), а в інших потрібно неодноразове уточнення постановки задачі, виділення головних визначальних чинників, відкидання чинників, які незначно впливають на результат і т.д..
Так, для задачі 1 математична модель може бути утворена, якщо врахувати наступні теоретичні відомості.
1. До характеристик власного руху коливальної ланки, яким є фізичний маятник, відносять:
1) частоту власних коливань;
2) коефіцієнт загасання цих коливань.
2. При малих відхиленнях від вертикалі рух маятника з достатньою точністю описується лінійним диференційним рівнянням другого порядку зі сталими коефіцієнтами:
![]() , (1.1)
, (1.1)
де ![]() - кут відхилення маятника від вертикалі;
- кут відхилення маятника від вертикалі; ![]() - момент інерції маятника відносно його осі обертання;
- момент інерції маятника відносно його осі обертання; ![]() - коефіцієнт демпфірування;
- коефіцієнт демпфірування; ![]() - маса маятника;
- маса маятника; ![]() - прискорення вільного падіння;
- прискорення вільного падіння; ![]() - зміщення центра мас маятника відносно осі його обертання;
- зміщення центра мас маятника відносно осі його обертання; ![]() - кутова швидкість повороту маятника навколо його осі обертання;
- кутова швидкість повороту маятника навколо його осі обертання; ![]() - кутове прискорення маятника.
- кутове прискорення маятника.
Похожие работы
... ї конференції молодих науковців CSE-2007. – Львів: Видавництво Національного університету "Львівська політехніка", 2007. – С.74–75. АНОТАЦІЇ Акимишин О.І. Методи та засоби зменшення обсягів даних тріангуляційного опису об’єктів комп’ютерної томографії. – Рукопис. Дисертація на здобуття наукового ступеня кандидата технічних наук за спеціальністю 05.13.05 – комп’ютерні системи та ...
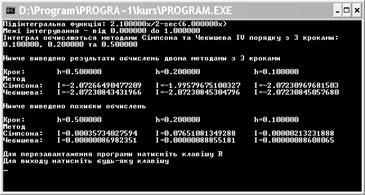
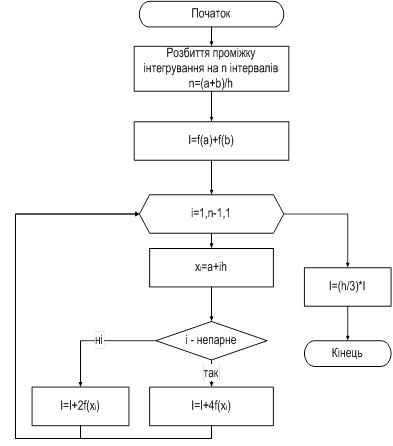
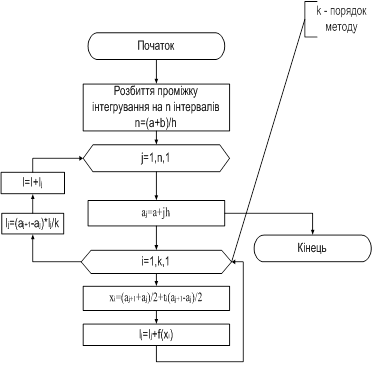
... програми Mathcad, рівне – 2,681. Нижче наведено результат роботи програми. Висновки В ході виконання даної курсової роботи було розглянуто методи чисельного інтегрування, а саме: Чебишева та Трапеції. Було досліджено вказані методи інтегрування та порівняно їх точності, розроблено програму на компіляторі Turbo C++, яка знаходить чисельне значення вказаного інтегралу. Таким чином були ...
... є f*, є рутинною вправою; отже, х-1 є обчислювана функція на Z. Приведене вище визначення очевидним образом розширюється на n-місцеві обчислювальні функції на області D і розв'язні предикати на D. 5. Алгоритмічні проблеми для L Нижче дається огляд нерозв'язних проблем, що виникають у самій теорії обчислювальності, і обговорюються деякі методи доказу нерозв'язності. Нагадаємо, що предикат ...
... (меньше 0,33%) одного з вільних членів системи (3) зовсім змінило розв’язок системи. На щастя, на практиці системи рівнянь, погано обумовлені, зустрічаються дуже рідко. 1.2 Методи розв’язування задачі Метод Жордана-Гаусса був розроблений двома вченими Жорданом та Гаусом (ві яких і пішла назва методу). Цей метод вони помітили після довгої практики роботи з системами рівнянь. Це можна ...
0 комментариев