Навигация
8. Кінець обчислень.
При виконанні алгоритму перехід від однієї дії до іншої здійснюється строго у порядку їхнього запису. Якщо ж потрібно перервати природний хід дій за деякої умови, слід указувати на це (див. п. 3 наведеного алгоритму).
Структурною схемою алгоритму називають графічне зображення послідовності дій обчислювального процесу.
У схемі кожна дія розміщується у певному геометричному символі (фігурі). Послідовність дій указується на схемі напрямком стрілок на лініях, якими з'єднують ці символи. Зазвичай прийнято початок і кінець обчислень зображувати овалами, введення даних і виведення результатів - у вигляді паралелограма. Обчислювальні операції розміщуються у прямокутниках, а операція перевірки деякої умови зображується у вигляді ромбу. Усередині кожної фігури розміщується стислий формульний опис відповідної операції.
Символи операцій перевірки умови мають два виходи: "так" і "ні". Стрілка на лінії, що виходить із виходу "так" вказує на операцію, до виконання якої потрібно перейти, якщо умову, яка перевіряється, виконано. Стрілка з написом "ні" вказує на операцію, до виконання якої слід перейти у випадку, коли умову не виконано.
На рис. 1.2. подані зображуючи елементи блок-схеми алгоритму обчислень. Фігури з'єднуються лініями зі стрілками, які вказують на операцію, до виконання якої слід перейти.
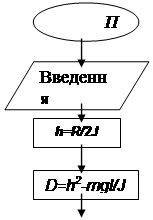
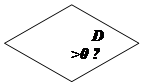
Для прикладу на рис 1.3 зображено схему алгоритму відшукування коренів квадратного рівняння.
- ![]() Початок (кінець) алгоритму
Початок (кінець) алгоритму
 | |||
![]() - Введення (виведення) даних
- Введення (виведення) даних
![]()
|
 | |||
так
![]() - Операція перевірки умови
- Операція перевірки умови
![]()
ні
Рис. 1.2 Елементи блок-схеми алгоритму
![]()
![]()
![]()
![]() ні
так
ні
так
|
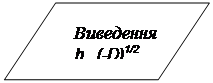

Рис. 1.3. Схема алгоритму відшукання коренів квадратного рівняння
1.5.3 Реалізація методу обчисленьОбчислення по алгоритмах відбувається за допомогою різних обчислювальних засобів.
При ручних (безпосередніх) розрахунках зазвичай використовуються найпростіші обчислювальні засоби: логарифмічна лінійка, таблиці, механічні, електричні, електронні клавішні обчислювальні машини. Проміжні результати дій алгоритму треба записувати у спеціальний розрахунковий бланк. Наявність програмувальних мікрокалькуляторів дозволяє реалізовувати обчислення автоматично, під керуванням програми.
Суттєвим є контроль обчислень, який проводять за так званим контрольним прикладом (тестом). Результат контрольного прикладу має бути заздалегідь відомим, тобто він або є очевидним, або його відшукують яким-небудь іншим способом. При ручному рахунку контроль рекомендується проводити поетапно. При розрахунках на ЕОМ за складеною програмою контрольний приклад заздалегідь прораховують вручну, а потім звіряють поетапно результати розрахунків із здійснюваними машиною.
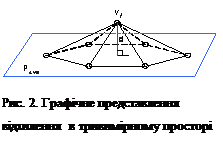
Розв’язання нелінійних рівнянь методом дихотомії Метод дихотомії (ділення навпіл)Алгоритм методу легко зрозуміти з мал.1
![]() y
y
![]()
 y=f(x)
y=f(x)
f(b)
![]() a f[(a+b)/2]
a f[(a+b)/2]

f(a) a+b b x
Мал.1 Схема методу дихотомії
Заданий інтервал ![]() ділиться навпіл. Цим знаходиться наближене значення
ділиться навпіл. Цим знаходиться наближене значення ![]() кореня. Обчислюється значення
кореня. Обчислюється значення ![]() функції при цьому значенні аргументу. Якщо воно дорівнює нулю,
функції при цьому значенні аргументу. Якщо воно дорівнює нулю, ![]() є точним значенням кореня й процес закінчується. Якщо ні, то визначається знак значення
є точним значенням кореня й процес закінчується. Якщо ні, то визначається знак значення ![]() . Обирається той інтервал, на межах якого задана функція набуває значень протилежного знаку. Наприклад, якщо виявиться, що
. Обирається той інтервал, на межах якого задана функція набуває значень протилежного знаку. Наприклад, якщо виявиться, що ![]() , то як нове значення верхньої межі інтервалу приймається
, то як нове значення верхньої межі інтервалу приймається ![]() :
: ![]() . У протилежному випадку змінюється нижня межа інтервалу
. У протилежному випадку змінюється нижня межа інтервалу ![]() . Далі процес повторюється для нового звуженого удвічі інтервалу
. Далі процес повторюється для нового звуженого удвічі інтервалу ![]() доти, поки значення похибки (5) не стане меншою за задане припустиме її значення
доти, поки значення похибки (5) не стане меншою за задане припустиме її значення
![]()
За остаточне значення кореня при цьому слід узяти значення (4).
Якщо обчислення потрібно проводити з максимальною точністю, процес звуження інтервалу слід продовжувати доти, поки нижня й верхня межі інтервалу ![]() не збіжаться у машинному поданні.
не збіжаться у машинному поданні.
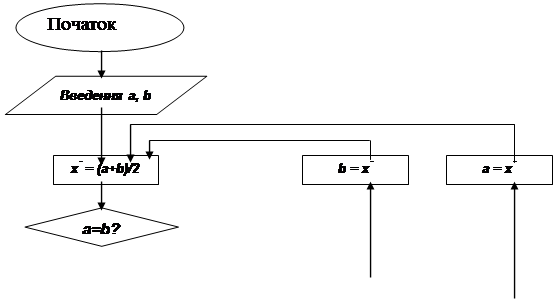
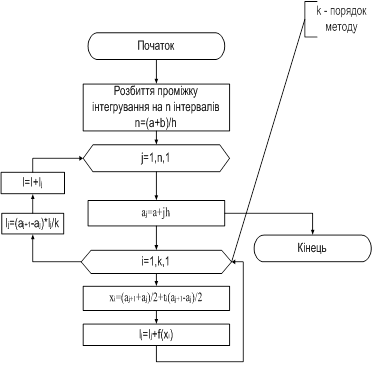
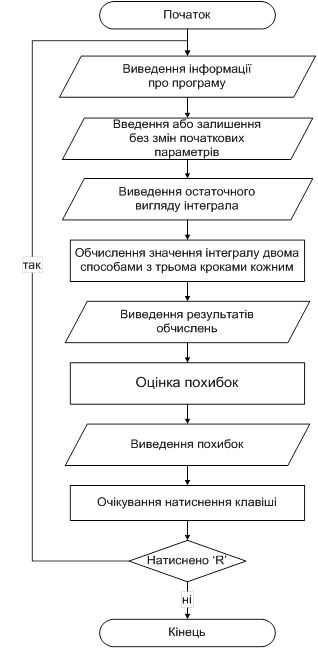
Схема алгоритму метода дихотомії для останнього випадку наведена на Мал.2.
![]()
![]() ні
ні
![]()
 так так ні
так так ні
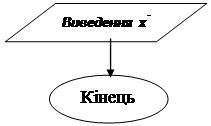 | |||||
Мал 2. Схема алгоритму метода дихотомії
До переваг метода дихотомії слід віднести те, що він може бути застосований навіть до тих неперервних функцій, що є недиференційованими у деяких точках усередині заданого інтервалу визначення кореня.
Список літератури
1. Бахвалов Н.С. и др. Численные методы. -М. : Наука, 1987.
2. Боглаев Ю.П. Вычислительная математика и программирование. -М.: Высшая школа, 1990.
3. Демидович Б.П. , Марон И.А. Основы вычислительной математики. -М. : Наука, 1970.
4. Войцехівський, І.П. Гаврилюк та ін. – К.: Вища шк., 1995, 303 с.
5. Воробьева Г.Н. , Данилова А.Н. Практикум по вычислительной математике. -М. : Высшая школа, 1990, 208.
6. Гаврилюк І.П., Макаров В.Л. Методи обчислень: Підручник: У 2ч. – К.: Вища шк., 1995. – Ч.1., 367 с.
7. Гаврилюк І.П., Макаров В.Л. Методи обчислень: Підручник: У 2ч. – К.: Вища шк., 1995. – Ч.2., 431 с.
8. Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. - М.: Мир, 1977.
Похожие работы
... ї конференції молодих науковців CSE-2007. – Львів: Видавництво Національного університету "Львівська політехніка", 2007. – С.74–75. АНОТАЦІЇ Акимишин О.І. Методи та засоби зменшення обсягів даних тріангуляційного опису об’єктів комп’ютерної томографії. – Рукопис. Дисертація на здобуття наукового ступеня кандидата технічних наук за спеціальністю 05.13.05 – комп’ютерні системи та ...
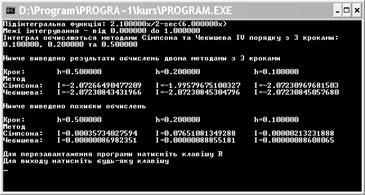
... програми Mathcad, рівне – 2,681. Нижче наведено результат роботи програми. Висновки В ході виконання даної курсової роботи було розглянуто методи чисельного інтегрування, а саме: Чебишева та Трапеції. Було досліджено вказані методи інтегрування та порівняно їх точності, розроблено програму на компіляторі Turbo C++, яка знаходить чисельне значення вказаного інтегралу. Таким чином були ...
... є f*, є рутинною вправою; отже, х-1 є обчислювана функція на Z. Приведене вище визначення очевидним образом розширюється на n-місцеві обчислювальні функції на області D і розв'язні предикати на D. 5. Алгоритмічні проблеми для L Нижче дається огляд нерозв'язних проблем, що виникають у самій теорії обчислювальності, і обговорюються деякі методи доказу нерозв'язності. Нагадаємо, що предикат ...
... (меньше 0,33%) одного з вільних членів системи (3) зовсім змінило розв’язок системи. На щастя, на практиці системи рівнянь, погано обумовлені, зустрічаються дуже рідко. 1.2 Методи розв’язування задачі Метод Жордана-Гаусса був розроблений двома вченими Жорданом та Гаусом (ві яких і пішла назва методу). Цей метод вони помітили після довгої практики роботи з системами рівнянь. Це можна ...
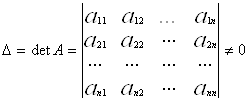
0 комментариев