Навигация
Анализ алгоритма Евклида
2. Анализ алгоритма Евклида
Прежде чем, приступить к анализу алгоритма Евклида рассмотрим числа Фибоначчи.
Суть последовательности Фибоначчи в том, что начиная с 1,1 следующее число получается сложением двух предыдущих.
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 ….
Приступим к анализу алгоритма Евклида. Нас будет интересовать наихудший случай — когда алгоритм работает особенно долго? Спросим точнее: какие два наименьших числа надо засунуть в алгоритм Евклида, чтобы он работал в точности заданное число шагов? Ответ на этот вопрос дает
Теорема (Ламэ, 1845 г.). Пусть n Î N , и пусть a > b > 0 такие, что алгоритму Евклида для обработки а и b необходимо выполнить точно n шагов (делений с остатком), причем а - наименьшее с таким свойством. Тогда а = F n +2 , b = F n +1 , где F k — k- ое число Фибоначчи.
Следствие. Если натуральные числа a и b не превосходят N Î N , то число шагов (операций деления с остатком), необходимых алгоритму Евклида для обработки a и b не превышает
é log Ф ( Ö 5 N ) ù - 2,
где é a ù - верхнее целое a , F = (1 + Ö 5)/2 — больший корень характеристического уравнения последовательности Фибоначчи.
log Ф ( Ö 5 N ) » 4,785 · lg N + 1,672, поэтому, например, с любой парой чисел, меньших миллиона, алгоритм Евклида разбирается не более, чем за é 4,785 · 6 + 1,672 ù - 3 = 31 - 3 = 28 шагов.
3. Евклидовы кольца
Неформально, евклидово кольцо — в абстрактной алгебре — кольцо, в котором «работает» алгоритм Евклида.
Примеры
· Кольцо целых чисел Z. Пример евклидовой функции — абсолютное значение ![]() .
.
· Кольцо целых гауссовых чисел Z[i] (где i — мнимая единица, i2 = − 1) с нормой d(a + ib) = a2 + b2 — евклидово.
· Произвольное поле K является евклидовым кольцом с нормой, равной 1 для всех элементов, кроме 0.
· Кольцо многочленов в одной переменной K[x] над полем K. Пример евклидовой функции — степень deg.
· Кольцо формальных степенных рядов K[[x]] над полем K является евклидовым кольцом. Норма степенного ряда — номер первого ненулевого коэффициента в нём (для нулевого ряда норма равна минус бесконечности).
· Евклидовыми являются кольца конечных двоичных и конечных десятичных дробей, так как они являются кольцами частных кольца целых чисел Z.
· Евклидовыми являются кольца рациональных функций над полем C с фиксированными полюсами, так как такие кольца являются кольцами частных кольца многочленов C[x].
4 Аналоги чисел Фибоначчи
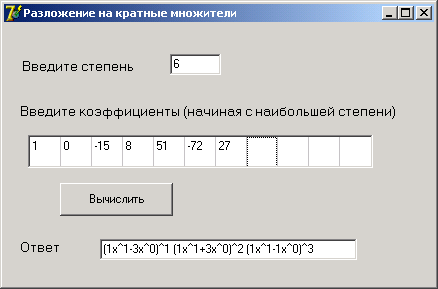
Мною были построены аналоги чисел Фибоначчи в кольце многочленов и исследованы некоторые их свойства. Для этих целей я использовала программу Mathematica 5.1.
Определение аналогов чисел Фибоначчи:
![]() ;
; ![]() ;
; ![]()
Первые 10 многочленов:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7.
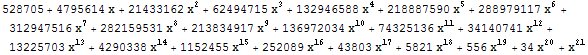 |
8.
9.
 |
10.

Заключение
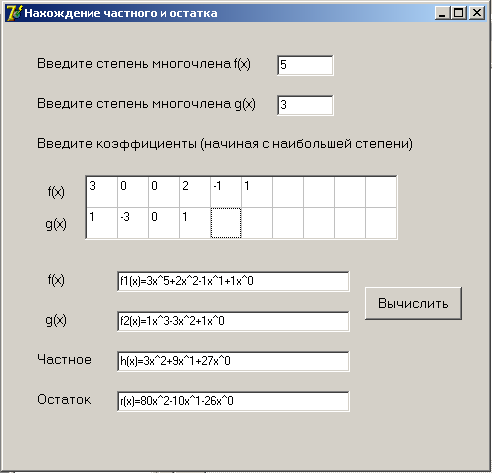
Данная работа посвящена расширенному алгоритму Евклида. Алгоритму Евклида более 2000 лет и он традиционно используется для нахождения наибольшего общего делителя натуральных чисел посредством остатков от деления.
Со временем алгоритм Евклида стали применять и в диафантовом анализе (для решения уравнений в целых числах), и в механизме цепных дробей (для наилучшего приближения действительных чисел рациональными), используется и для быстрого возведения в степень в компьютерных алгоритмах, и в криптографии.
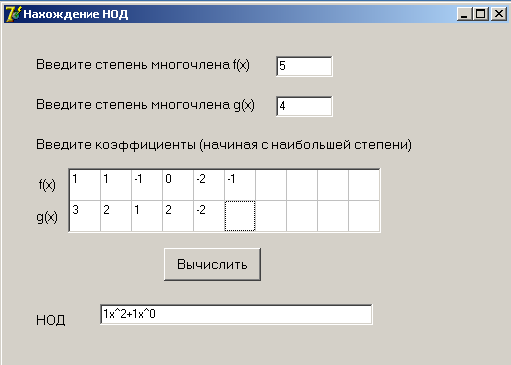
Как было показано, числа Фибоначчи обладают экстремальным свойствам: при подстановке в алгоритм Евклида чисел Фибоначчи с номерами n и n+1, алгоритм выполняется за n шагов.
В своей работе я нашла многочлены обладающие теми же свойствами. В дальнейшем я планирую исследовать свойства этих многочленов и построить степенные ряды, обладающие теми же свойствами.
Список использованных источников
1. С. Ленг, Алгебра, М., 1968
2. С. Коунтинхо, Введение в теорию чисел. Алгоритм RSA, – М. 2001
3. Н.М. Бескин, Замечательные дроби, –М.,1980 г.
4. А.И. Кострикин, Введение в алгебру, – М., 2000
5. Энциклопедия для детей Аванта + «математика» том 11 2002 г.
6. О. Зарисский, Коммутативная алгебра, т.1.,– М., 1963
7. Л.Я. Куликов, Алгебра и теория чисел – М.,1979 г.
8. А.Г. Цыпкин, Справочник по математике для средних учебных заведений, – 1984 г.
9. А.П. Савин, Я познаю мир. Сер. «Математика» / А.П. Савин, В.В. Станцо, А.Ю. Котова, – М. 2006 г.
Похожие работы
... из которых мультипликативна по лемме 2 пункта 13. Значит, ( a ) - мультипликативна. Следствие 3. . Доказательство. Пусть . Тогда, по лемме 1 пункта 13 имеем: . 5 Китайская теорема об остатках В этом пункте детально рассмотрим только сравнения первой степени вида ax b(mod m), оставив более высокие степени на съедение следующим ...
... самом деле, в качестве наибольшего общего делителя двух взаимно простых многочленов можно взять любое число, отличное от нуля, но, умножая его на обратный элемент, получим единицу. Применяя алгоритм Евклида к многочленам с целыми коэффициентами, можем, чтобы избежать дробных коэффициентов, умножить делимое или сократить делитель на любое не равное нулю число, причем не только начиная какое-либо ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
... об остатках (КТО). Теорема. Пусть – попарно взаимно простые числа, = , , , …, подобраны так, что 1, = , . Тогда решение системы , , будет иметь вид: . Эта теорема лежит в основе метода ортогональных базисов при переводе из системы остаточных классов в позиционную систему счисления. Пусть основания системы остаточных классов ; = = – объем диапазона системы. С выбором системы определяются ее ...
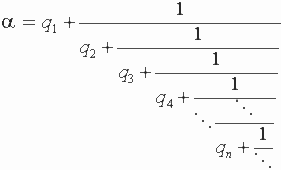
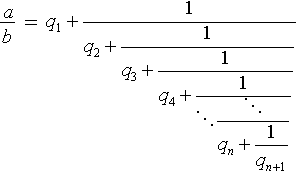
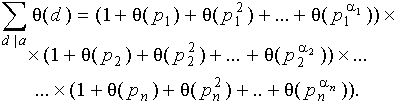



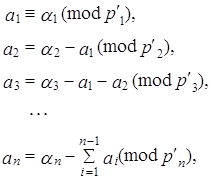
0 комментариев