Навигация
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Авиа- и ракетостроение»
Специальность 160801- «Ракетостроение»
Расчетно-графическая работа
по дисциплине «Основы САПР»
Аппроксимация функций
Омск 2006
Введение
Цель работы: Ознакомиться с методами интерполяции и аппроксимации функций
Задания:
Задание 1. Построить таблицу конечных разностей. Выполнить экстраполяцию на два узла от начала и от конца таблицы.
Задание 2. Построить интерполяционный многочлен Лагранжа и с его помощью найти
значения функции в узлах, соответствующих полушагу таблицы.
Задание 3. Найти значение f(x) с помощью формул Ньютона интерполирования вперед и назад.
Задание 4. Выполнить квадратичную сплайн-интерполяцию (по 6 узлам). Проконтролировать полученные оценки для промежуточных узлов.
Задание 5. Считая выбранную таблицу заданной для диапазона от 0 до 2, выполнить среднеквадратическую аппроксимацию тригонометрическим многочленом (отрезком ряда Фурье) третьей степени.
Исходные данные:
x=[11.0 11.1 11.2 11.3 11.4 11.5 11.6 11.7 11.8 11.9 12];
y=[-0.00023,1.080087,2.064282,2.854531,3.37121,3.560925,3.402017,2.90698,2.121544,1.120452,0.000357];
1. Построение массива конечных разностей. Выполнение экстраполяции
Массив конечных разностей рассчитываем по формуле:
![]() .
.
for i=1:10
for j=1:11-i
y(i+1,j)=y(i,j+1)-y(i,j);
end
end
Результат расчёта:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 11,0 11,1 11,2 11,3 11,4 11,5 11,6 11,7 11,8 11,9 11,0 | -0,0002 1,0801 2,0643 2.8545 3.3712 3.5609 3.4020 2.9070 2.1215 1.1205 0.0004 | 1.0803 0.9842 0.7902 0.5167 0.1897 -0.1589 -0.4950 -0.7854 -1.0011 -1.1201 - | -0.0961 -0.1939 -0.2736 -0.3270 -0.3486 -0.3361 -0.2904 -0.2157 -0.1190 - - | -0.0978 -0.0796 -0.0534 -0.0217 0.0125 0.0457 0.0747 0.0967 - - - | 0.0182 0.0262 0.0317 0.0342 0.0332 0.0290 0.0219 - - - - | 0.0080 0.0055 0.0024 -0.0009 -0.0042 -0.0071 - - - - - | -0.0025 -0.0031 -0.0033 -0.0033 -0.0029 - - - - - - | -0.0006 -0.0002 0.0000 0.0004 - - - - - - - | 0.0003 0.0003 0.0004 - - - - - - - - | -0.0000 0.0001 - - - - - - - - - | 0.0002 - - - - - - - - - - |
Экстраполяция на два узла от начала и конца таблицы с помощью многочлена Лагранжа.
n=11; % Степень многочлена
i=0;
for p=10.8:0.1:12.2
i=i+1;
x1(i)=p;
ff(i)=Lagrange(x,y,p,n);
end
for j=1:11
yy(j)=y(1,j);
end
subplot(2,1,1); plot(x,yy,'.-'); ylabel('y'); xlabel('x'); grid on; title('Первоначальные данные')
subplot(2,1,2); plot(x1,ff,'.-'); ylabel('y'); xlabel('x'); grid on; title('Экстраполяция')
Получим:
| х | 10.8 | 10.9 | 12.1 | 12.2 |
| f(х) | -2,0234 | -1,0701 | -1,1291 | -2,1535 |
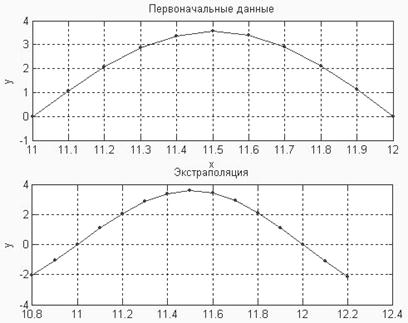
Рис. 1. Экстраполяция на два узла многочленом Лагранжа
Похожие работы
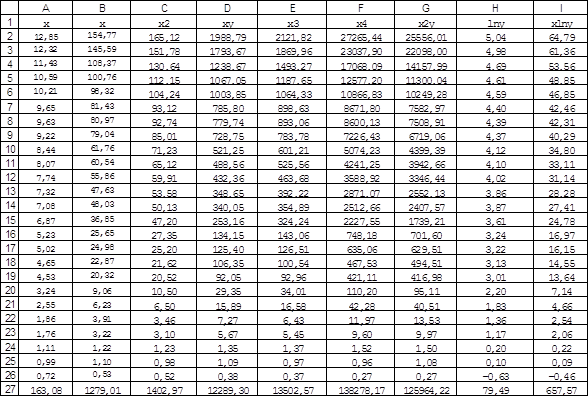
... считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные. 3. Расчет коэффициентов аппроксимации в Microsoft Excel. Вариант №22 Функция y=f(x) задана таблицей 1 Таблица 1 Исходные данные. 12.85 154.77 9.65 81.43 7.74 55.86 5.02 24.98 1.86 3.91 12.32 145.59 9.63 80.97 7.32 ...
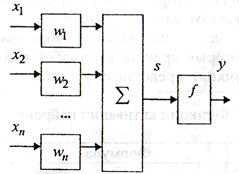
... необходимо построить и обучить нейронную сеть для аппроксимации таблично заданной функции yi=f(xi)=[2.09 2.05 2.19 2.18 2.17 2.27 2.58 2.73 2.82 3.04 3.03 3.45 3.62 3.85 4.19 4.45 489 5.06 5.63 5.91], i=1,20. В математической среде Matlab создаем новый M-File, в котором записываем код программы создания и обучения нейронной сети с использованием встроенных функций пакета сетей Neural Netwworks ...
... [a,b]. Теперь мы можем рассматривать функции в произвольных нормированных пространствах. III. Методы аппроксимации 3.1 Приближение функций многочленами. Алгебраическим многочленом степени n называется функция - действительные числа, называемые коэффициентами. Алгебраические многочлены являются простейшими функциями. Они непрерывны при любом x. Производная многочлена- так же многочлен, степень ...
... 368.0 3354.0 159.0 368.0 3354.0 33428.0 1023.0 Вектор коэфициентов аппроксимирующего многочлена по возрастанию степени (m+1 элементов) a[1]= 11.66 a[2]= -2.31 a[3]= 0.13 Вектор погрешности аппроксимации в узлах X z[1]=0.479 z[2]=-1.381 z[3]=-1.343 z[4]=-1.070 z[5]=-1.247 z[6]=-1.430 z[7]=-0.244 z[8]=0.723 z[9]=3.570 z[10]=1.454 5.1 Список переменных основной программы. ...
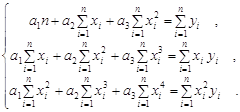
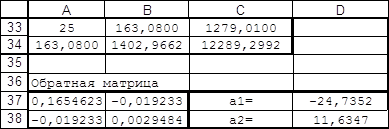
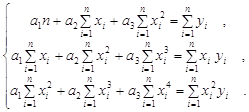


0 комментариев