Навигация
Введение в математический анализ
14503
знака
0
таблиц
6
изображений
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственный технический университет
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Учебное пособие по математике
для студентов всех специальностей
заочной формы обучения
2007
ФУНКЦИЯ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ
Основные определения и понятия
Одним из основных понятий математики является число. Числа целые и дробные, как положительные, так и отрицательные, вместе с числом ноль называются рациональными числами. Рациональные числа могут быть представлены в виде конечных или бесконечных периодических дробей. Числа, которые представляются в виде бесконечных, но непериодических дробей, называются иррациональными.
Совокупность всех рациональных и иррациональных чисел называется множеством действительных, или вещественных чисел. Действительные числа можно изображать точками числовой оси. Числовой осью называется бесконечная прямая, на которой выбраны:
1) некоторая точка О, называемая началом отсчёта;
2) положительное направление, указываемое стрелкой;
3) масштаб для измерения длин.
Между всеми действительными числами и всеми точками числовой оси существует взаимно–однозначное соответствие, т.е. каждому действительному числу соответствует точка числовой оси и наоборот.
Абсолютной величиной (или модулем) действительного числа x называется неотрицательное действительное число ׀x׀, определяемое следующим образом: ׀x׀ = x, если x ≥ 0, и ׀x׀ = –x, если x < 0.
Переменной величиной называется величина, которая принимает различные численные значения. Величина, численные значения которой не меняются, называется постоянной величиной.
Переменная величина называется упорядоченной, если известна область её изменения и про каждое из двух любых её значений можно сказать, какое из них предыдущее и какое последующее. Частным случаем такой величины является числовая последовательность 
Переменная величина называется возрастающей (убывающей), если каждое её последующее значение больше (меньше) предыдущего. Возрастающие и убывающие переменные величины называются монотонными. Переменная величина называется ограниченной, если существует такое постоянное число M > 0, что все последующие значения переменной, начиная с некоторого, удовлетворяют условию:
– M ≤ x ≤ M, т.е. ׀x׀ ≤ M.
Переменная величина y называется (однозначной) функцией переменной величины x, если каждому значению переменной величины x, принадлежащему множеству действительных чисел X, соответствует одно определённое действительное значение переменной величины y.
Переменная x называется в этом случае аргументом, или независимой переменной, а множество X – областью определения функции.
Запись y = f(x) означает, что y является функцией x. Значение функции f(x) при x = a обозначают через f(a).
Область определения функции в простейших случаях представляет собой: интервал (открытый промежуток) (a, b), т.е. совокупность значений x, удовлетворяющих условию a < x < b; сегмент (отрезок или замкнутый промежуток) 
, т.е. совокупность значений x, удовлетворяющих условию a ≤ x ≤ b; полуинтервал
(т.е. a < x ≤ b) или 
(т.е. a ≤ x < b); бесконечный интервал (a, + ∞) (т.е. a < x < + ∞) или (– ∞, b) (т.е. – ∞ < x < b) или (– ∞, + ∞) (т.е. – ∞ < x < + ∞); совокупность нескольких интервалов или сегментов и т. п.
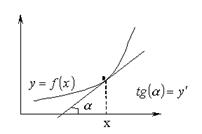
Графиком функции y = f(x) называется геометрическое место точек плоскости xOy, координаты которых удовлетворяют уравнению y = f(x).
Функция f(x) называется чётной, если 
для любого значения x. График чётной функции расположен симметрично относительно оси ординат. Функция f(x) называется нечётной, если 
для любого значения x. График нечётной функции расположен симметрично относительно начала координат.
Функция f(x) называется периодической, если существует такое положительное число T, называемое периодом функции, что для любого значения x выполняется равенство 
.
Наименьшим же периодом функции называется наименьшее положительное число τ, для которого f(x + τ) = f(x) при любом x. Следует иметь в виду, что f(x + kτ) = f(x), где k – любое целое число.
Функции задаются:
1) аналитически (в виде формулы), например, 
;
2) графически (в виде графика);
3) таблично (в виде таблицы), например таблица логарифмов.
Основными элементарными функциями являются следующие, аналитически заданные функции:
1. Степенная функция: 
, где α – действительное число.
2. Показательная функция: 
, где a > 0, a ≠ 1.
3. Логарифмическая функция: 
, где a > 0, a ≠ 1.
Похожие работы
... в соответствии с вариантом, выбираемым по последней цифре номера зачетной книжки в отдельной тетради. Каждая задача должна содержать условие, подробное решение и вывод. 1. Введение в математический анализ Задача 1. Найти область определения функции. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Задача 2. Найти пределы функций. . Задача 3. Найти ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... Строгое определение предела дается сначала для функций частного вида – последовательностей, а затем переносится на функции общего вида. На основе понятия предела определяются важнейшие понятия математического анализа – производная и интеграл. Предел последовательности Последовательностью называется функция, определенная на множестве натуральных чисел N = . Значения этой функции , N, называются ...
... образования не вызывает сомнения. Вопрос о том, каким быть математическому образованию в XXI веке, является чрезвычайно важным. Что может дать гуманитаризация математическому образованию? Ответ на этот вопрос окажет влияние на все будущее России. Недостатком педагогических теорий по реформированию математического образования является их неконкретность и расплывчатость. Математикам самим следует ...
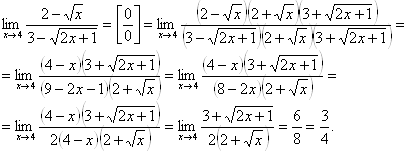
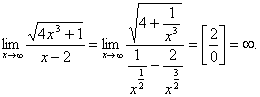
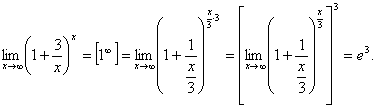
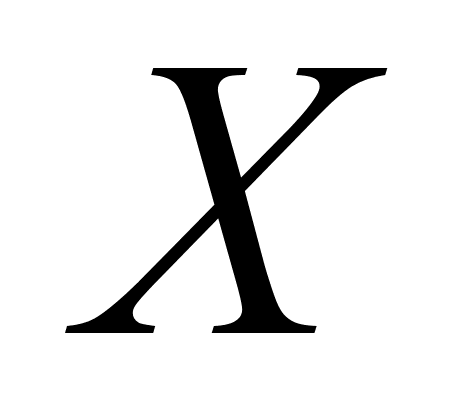
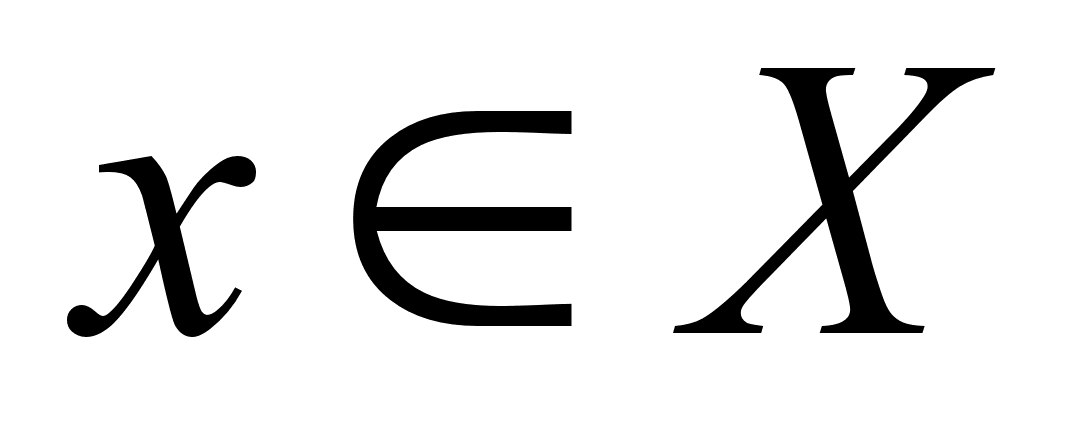
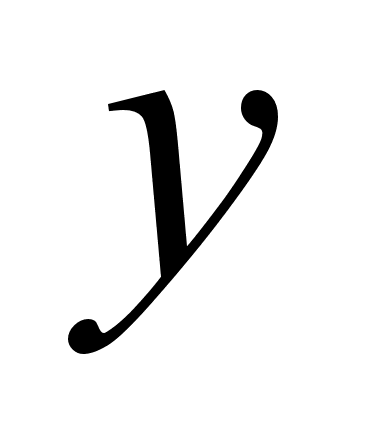
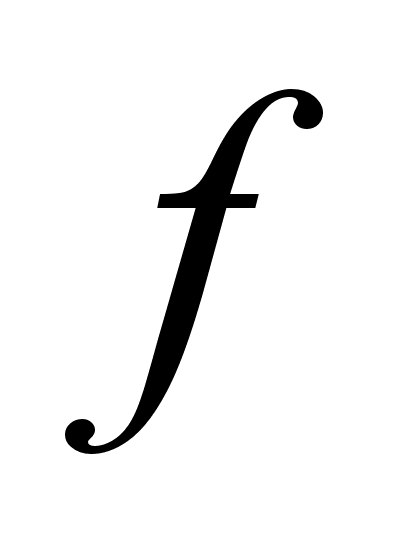
0 комментариев