Навигация
Числовые функции
Понятие функции является одним из основных в математике. С его помощью выражают зависимости между различными переменными величинами. Изучение свойств функций, основанное на методе пределов, составляет содержание математического анализа.
Определение
Пусть ![]() -
некоторое
числовое множество,
и пусть каждому
элементу
-
некоторое
числовое множество,
и пусть каждому
элементу ![]() поставлено
в соответствие
число
поставлено
в соответствие
число ![]() .
Тогда говорят,
что на множестве
.
Тогда говорят,
что на множестве
![]() определена
числовая функция.
Функцию обозначают
некоторым
символом, например
определена
числовая функция.
Функцию обозначают
некоторым
символом, например
![]() ,
и пишут
,
и пишут
![]() . (1)
. (1)
Множество
![]() называется
областью
определения
функции
называется
областью
определения
функции ![]() ,
,
![]() - ее аргументом,
а
- ее аргументом,
а ![]() - значением
функции в точке
- значением
функции в точке
![]() .
Используются
также обозначения:
.
Используются
также обозначения:
![]() для области
определения
и
для области
определения
и ![]() для множества
значений функции.
для множества
значений функции.
Графиком
функции ![]() называется
множество всех
точек координатной
плоскости вида
называется
множество всех
точек координатной
плоскости вида
![]() ,
где
,
где ![]() .
График дает
наглядное
представление
о поведении
функции, однако
более удобным
в теоретических
исследованиях
является
аналитический
способ задания
функций с помощью
формул. На практике
используют
также табличный
способ, когда
значения функции
указываются
для отдельных
значений аргумента.
.
График дает
наглядное
представление
о поведении
функции, однако
более удобным
в теоретических
исследованиях
является
аналитический
способ задания
функций с помощью
формул. На практике
используют
также табличный
способ, когда
значения функции
указываются
для отдельных
значений аргумента.
В качестве области определения функции могут выступать различные числовые множества, например:
а) отрезок ![]() ;
;
б) интервал
![]() ;
;
в) полуинтервалы
![]() или
или ![]() ;
;
г) бесконечные
полуинтервалы
![]() или
или ![]() ;
;
д) множество
всех действительных
чисел R =![]() .
.
Под областью определения функции, заданной формулой, понимают обычно множество всех значений аргумента, для которых эта формула имеет смысл.
Примеры.
1) Для функции
![]() область определения
и множество
значений
область определения
и множество
значений
имеют
вид: ![]() ,
,
![]() ;
график функции
представлен
на рис. 1.
;
график функции
представлен
на рис. 1.
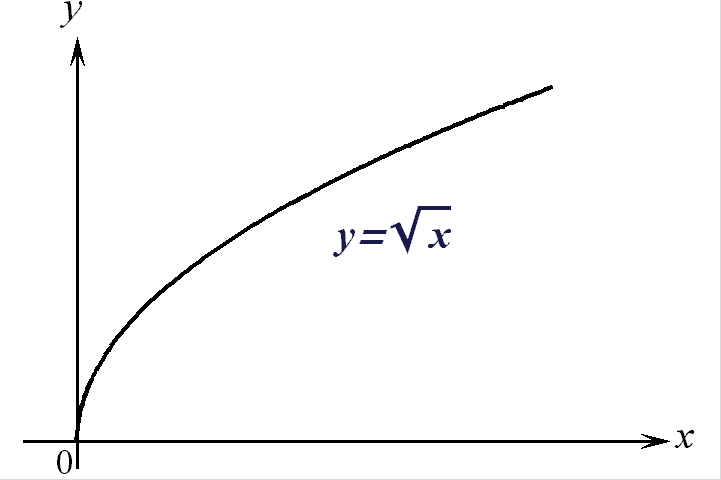
Рис. 1.
2)
Для функции
![]() имеем
имеем
![]() ,
,
![]() ;
график функции
изображен на
рис. 2.
;
график функции
изображен на
рис. 2.
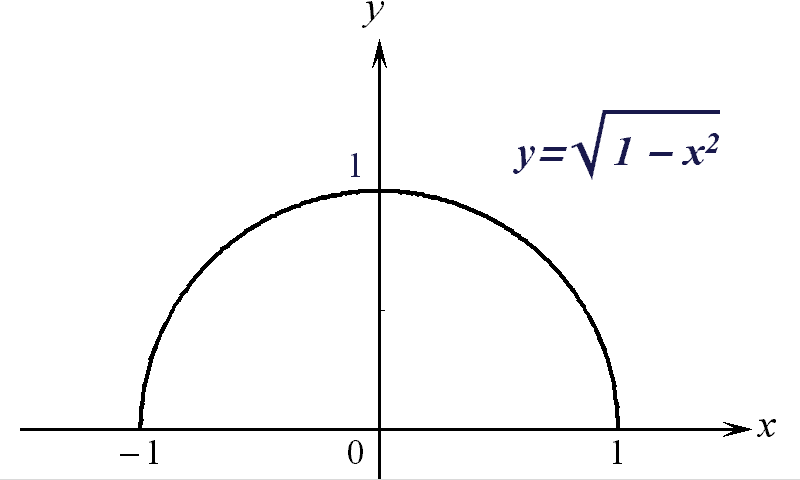
Рис. 2.
3) Для функции
![]() имеем:
имеем: ![]() ,
,
![]() ;
ее график приведен
на рис. 3.
;
ее график приведен
на рис. 3.
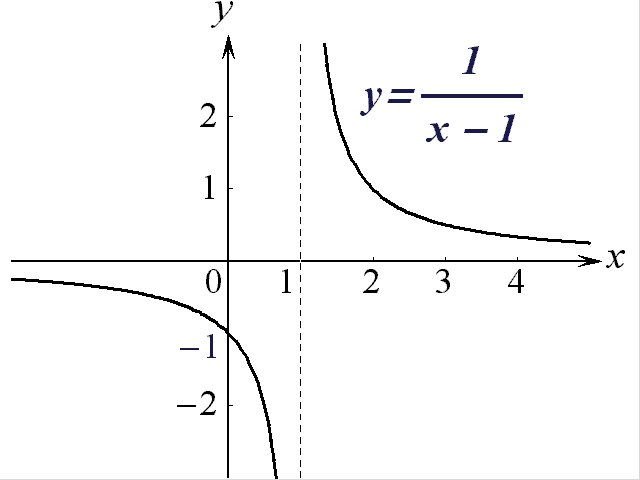
Рис. 3.
Основные элементарные функций
Напомним определения и свойства некоторых элементарных функций, известные из школьного курса математики. В каждом случае укажем аналитическое выражение и область определения функции, приведем ее график.
а) Линейная функция:
![]() R,
R,
где ![]() и
и ![]() – некоторые
постоянные
(числа); график
– прямая с угловым
коэффициен-
– некоторые
постоянные
(числа); график
– прямая с угловым
коэффициен-
том ![]() (
(![]() ,
где
,
где ![]() – угол наклона
прямой к оси
– угол наклона
прямой к оси
![]() ):
):
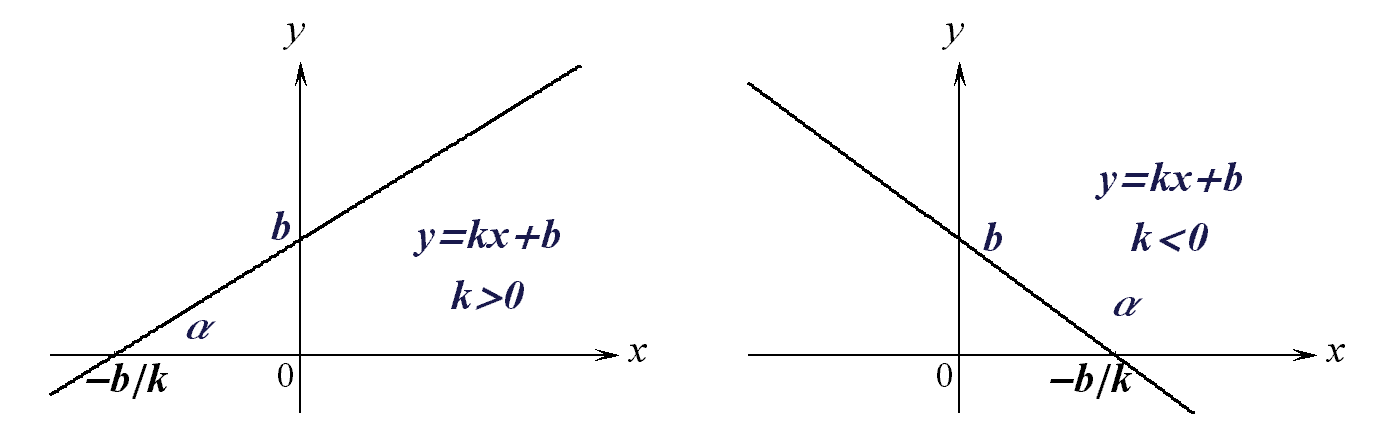
Рис.4.
б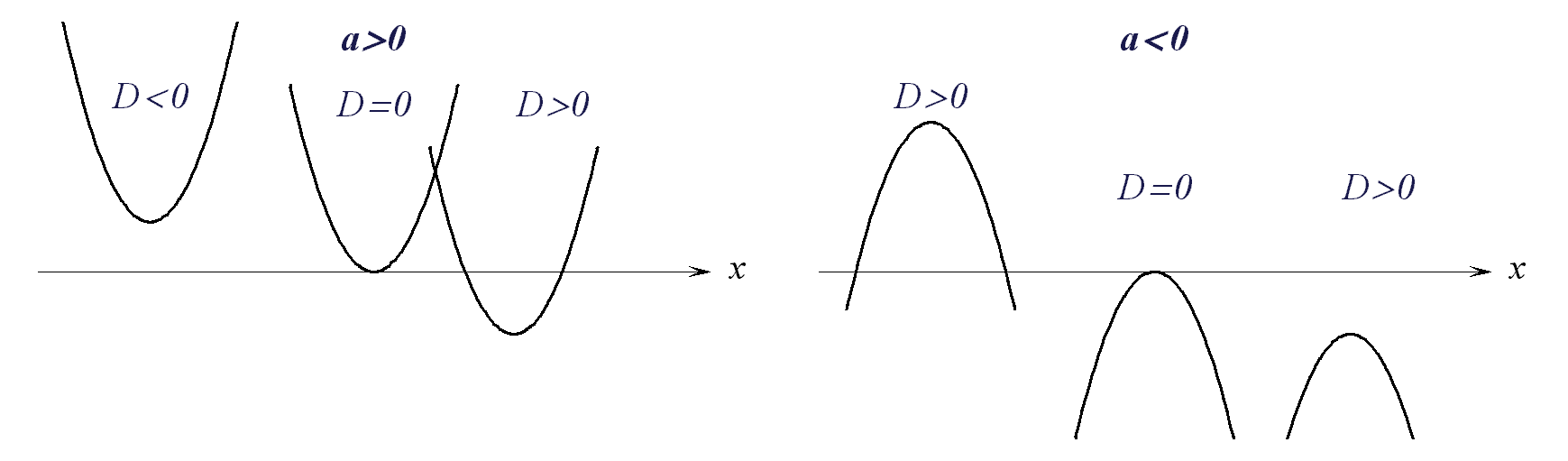
)
Квадратичная
функция:
![]() R,
R,
Рис. 5.
где
![]() ,
,
![]() ,
,
![]() - постоянные
коэффициенты;
график – парабола,
ее расположение
существенно
зависит от
величины
- постоянные
коэффициенты;
график – парабола,
ее расположение
существенно
зависит от
величины
![]() ,
,
называемой
дискриминантом
функции, и от
знака первого
коэффициента
![]() :
:
в) Обратно пропорциональная зависимость:
![]() ,
,
где ![]() - постоянная.
График – гипербола:
- постоянная.
График – гипербола:
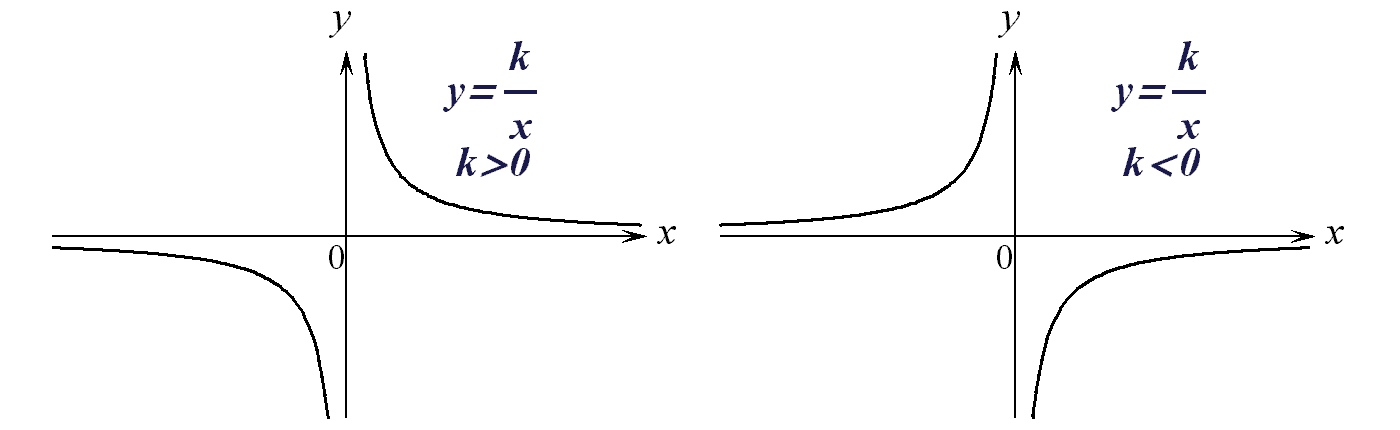
Рис. 6.
г) Степенная функция:
![]() ,
,
где ![]() и
и ![]() - постоянные;
область определения
существенно
зависит от
- постоянные;
область определения
существенно
зависит от ![]() .
В п. в) рассмотрен случай
.
В п. в) рассмотрен случай ![]() ,
а в примере 1 -
случай
,
а в примере 1 -
случай ![]() .
Приведем еще
графики функций
для
.
Приведем еще
графики функций
для ![]() и
и ![]() :
:
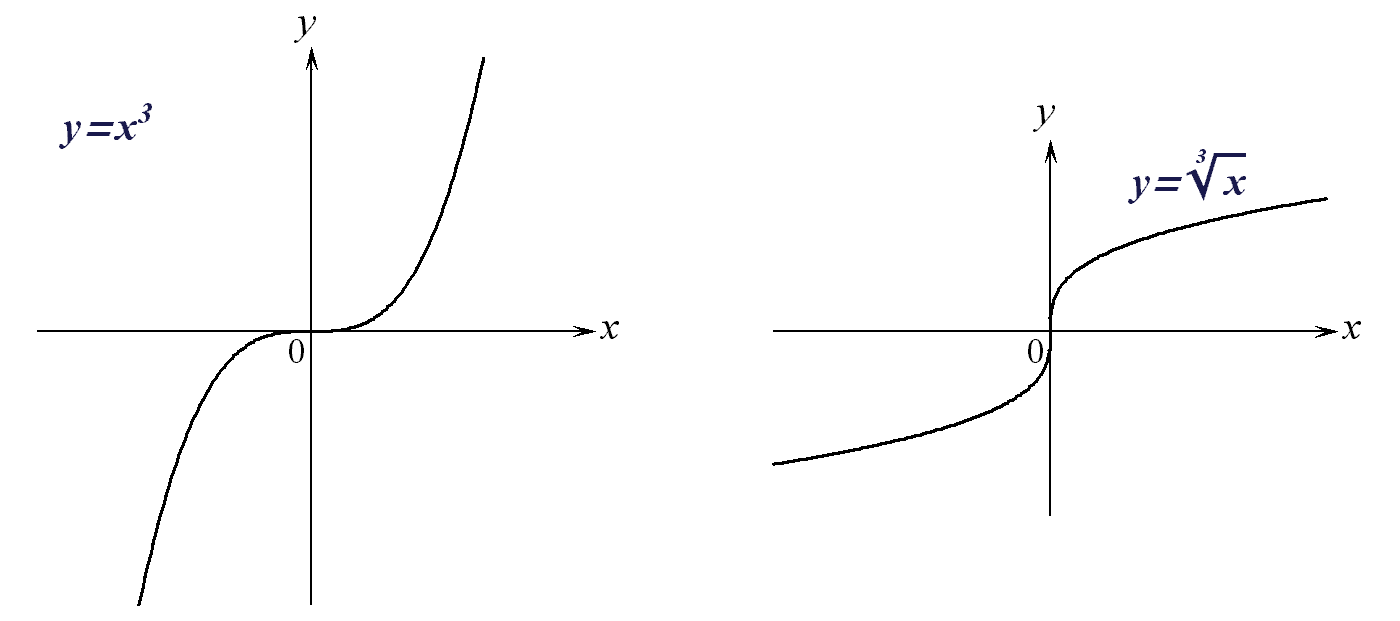
Рис. 7.
е) Показательная функция:
![]() R,
R,
где ![]() - постоянная;
график в зависимости
от значения
- постоянная;
график в зависимости
от значения
![]() имеет вид:
имеет вид:
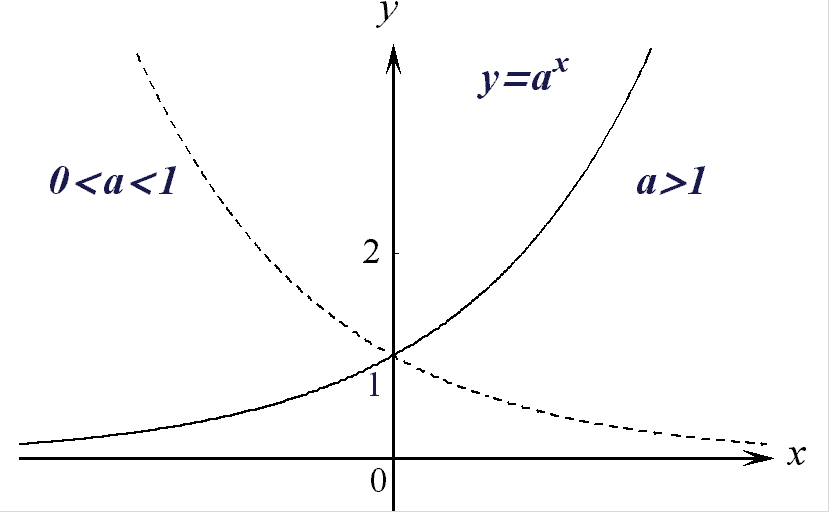
Рис. 8.
Все перечисленные здесь функции, а также логарифмическая, тригонометрические и обратные тригонометрические функции основными элементарными функциями.
Сложная функция
Пусть заданы
функции ![]() и
и ![]() ,
причем множество
значений функции
,
причем множество
значений функции
![]() принадлежит
области определения
функции
принадлежит
области определения
функции ![]() :
:
![]() .
Тогда можно
определить
сложную функцию
.
Тогда можно
определить
сложную функцию
![]() ,
,
называемую
также композицией
функций ![]() и
и ![]() .
.
Пример.
Из функций ![]() и
и ![]() с помощью указанной
операции можно
составить две
сложные функции:
с помощью указанной
операции можно
составить две
сложные функции:
![]() и
и
![]() .
.
Используя операцию композиции, можно из основных элементарных функций, получать новые функции, также называемые элементарными. Вообще, элементарной функцией называют функцию, которую можно получить из основных элементарных функций с помощью конечного числа арифметических операций и композиций.
П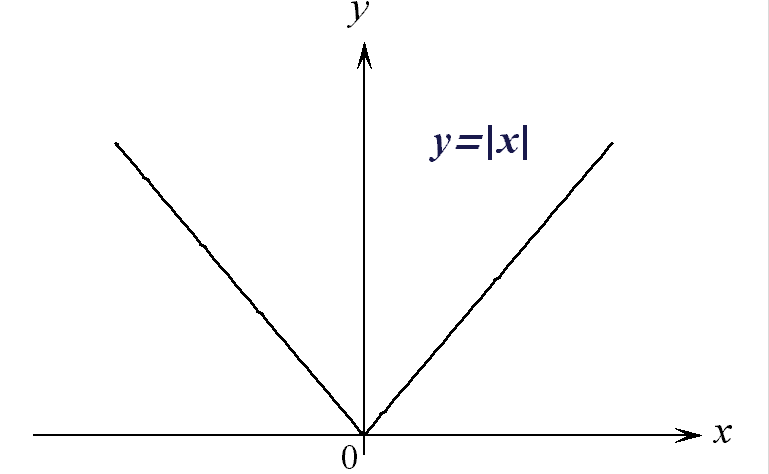
ример.
Функция 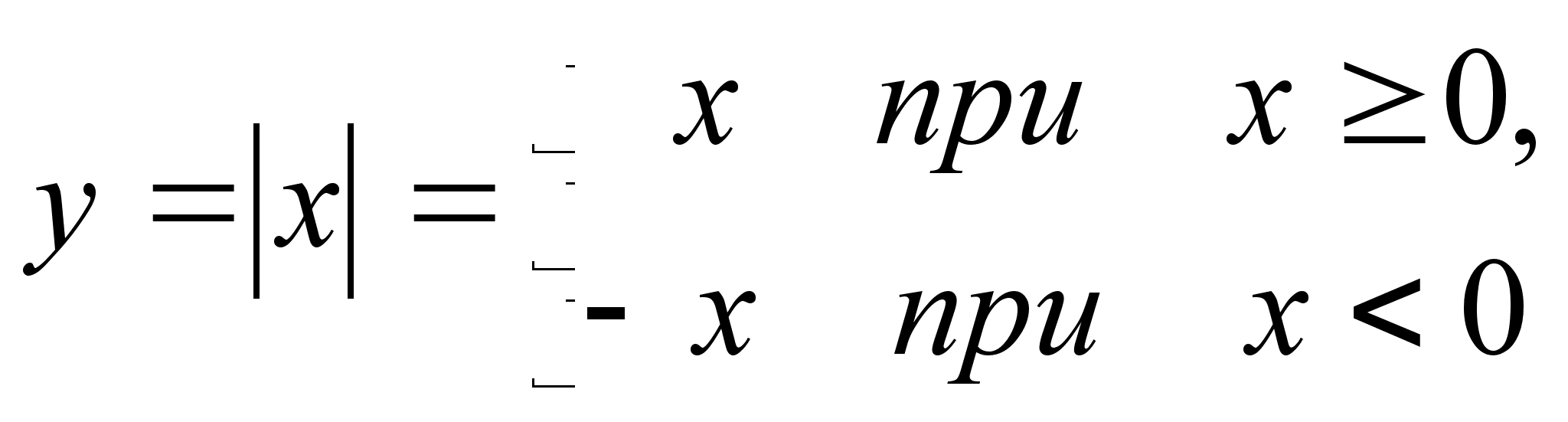 (читается: “модуль
(читается: “модуль ![]() ”)
является
элементарной,
так как для
всех
”)
является
элементарной,
так как для
всех ![]() R
справедливо
представление
R
справедливо
представление
![]() .
График этой
функции приведен
на рис. 9.
.
График этой
функции приведен
на рис. 9.
Рис. 9.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
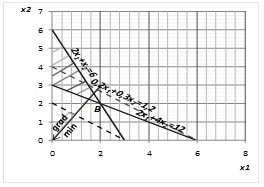
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





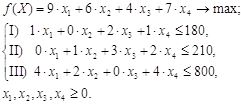
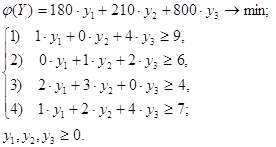
0 комментариев