Навигация
Визуализация численных методов
Сибирский государственный университет телекоммуникации и информатики
Уральский технический институт связи и информатики
Факультет телекоммуникации, информатики и управления
Кафедра организации управления связи
По курсу: “Информатика”
По теме: “Визуализация численных методов”
Написал:
Плишкин М. Ю
группа МЕ-72
Преподаватель:
Кандидат технических наук , доцент
Е.Е.Минина
г. Екатеринбург. 2010 г.
Содержание
Введение
1. Постановка задачи
1.1 Метод Эйлера
1.2 Метод Рунге – Кутта
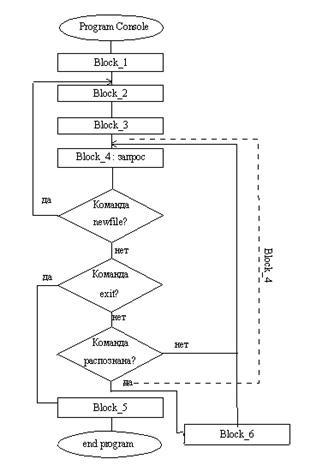
2. Блок-схемы
3. Виды, формы
3.1 Начальная форма
3.2 Конечная форма
4. Программа для решения дифференциального уравнения в Visual Basic
Заключение
Введение
Уравнения, связывающие независимую переменную, искомую функцию и её производные называют дифференциальным уравнением. Решение дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Если искомая (неизвестная) функция зависит от одной переменной, то дифференциальное уравнение называется обычным; в противном случае – уравнение в частных производных, содержащие несколько независимых переменных и производные по ним, которые называются частными. В данной работе будут рассматриваться методы решения обычных дифференциальных уравнений (ОДУ).
Чтобы решить ОДУ, необходимо знать значение зависимой переменной и (или) её производные при некоторых значениях независимой переменной. Если эти дополнительные условия задаются при одном значении независимой переменной, то такая задача называется задачей с начальными условиями, или задачей Коши.
Числовое решение задачи Коши широко применяется в различных областях науки и техники, и число разработанных для него методов достаточно велико. Эти методы могут быть разделены на следующие группы.
Одношаговые методы, в которых для нахождения следующей точки на кривой y=f(x) требуется информация лишь об одном предыдущем шаге. Одношаговыми являются метод Эйлера и методы Рунге – Кутта.
Методы прогноза и коррекции (многошаговые), в которых для отыскивания следующей точки кривой y=f(x) требуется информация более чем об одной из предыдущих точек. Чтобы получить достаточно точное численное значение, часто прибегают к итерации. К числу таких методов относятся методы Милны, Адамса – Башфорта и Хемминга.
Явные методы, в которых функция Ф в выражении (1) не зависит от yn+1.
Неявные методы, в которых функция Ф зависит от yn+1.
В данной курсовой работе будут рассматриваться два одношаговых метода: метод Эйлера первого порядка точности и Рунге – Кутта четвёртого порядка точности.
1. Постановка задачи
В данной курсовой работе необходимо решить ОДУ вида y` = 4y/x с заданными начальными значениями x0=1, xk=1.4, y0=2, h=0.05. Для проверки точности результатов дано общее решение данного уравнения y=x^4с. Требуется решить уравнение двумя методами: Эйлера модифицированного и Рунге – Кутта четвёртого порядка, сравнить результаты и сделать вывод какой метод эффективнее использовать, построить графики.
Численное решение задачи Коши сводится к табулированию искомой функции.
График решения дифференциального уравнения называется интегральной кривой.
Геометрический смысл задачи:
y`=f(x,y) – тангенс угла наклона касательной к графику решения в точке (x,y) к оси OX (угловой коэффициент (в общей формуле прямой,
y=k*x+b,
обозначается как “k”)(рис 1).
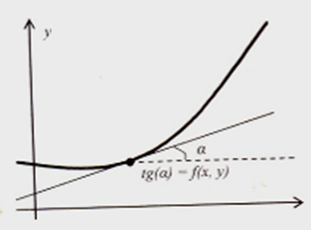
Рисунок 1. Геометрический смысл задачи Коши
Существующие решения:
Если правая часть f(x,y) непрерывная в некоторой области R, определяемой неравенствами |x – x0| < a; |y – y0| > b, то существует, по меньшей мере, одно решение y=y(x), определённое в окрестности |x – x0| < h, где h > 0.
При использовании численных методов выполняется замена отрезка [x0,X] – области непрерывного изменения аргумента x множеством wh, состоящего из конечного числа точек x0<x1<...<xn=X – сеткой.
При этом xi называют узлами решётки.
Задача Коши, определённая ранее на непрерывном отрезке [x0,X], заменяется её дискретным аналогом – системой уравнений, решая которую можно последовательно найти значения y1,y2,...,yn – приближённые значения функции в узлах сетки.
![]()
1.1 Метод Эйлера
Данный метод, как сказано выше, является одношаговым. Табулирование функции происходит поочередно в каждой точке. Для расчёта значения функции в очередном узле необходимо использовать значение функции в одном предыдущем узле.
Пусть дано дифференциальное уравнение первого порядка
y`=f(x,y)
с начальным условием
y(x0)=y0.
Выберем шаг h и введём обозначения:
xi=x0+i*h и yi=y(xi), где i=0,1,2,...,
xi- узлы сетки,
yi- значение интегральной функции в узлах.
Иллюстрации к решению приведены на рисунке 2.
Проведём прямую АВ через точку (xi,yi) под углом α. При этом
tgα=f(xi,yi) (1)
В соответствии с геометрическим смыслом задачи, прямая АВ является касательной к интегральной функции. Произведём замену точки интегральной функции точкой, лежащей на касательной АВ.
Тогда
y i+1=yi+Δy (2).
Из прямоугольного треугольника АВС
tgα= Δy/h (3).
Приравниваем правые части (1) и (3). Получим
Δy/h= f(xi,yi).
Отсюда
Δy= f(xi,yi)*h.
Подставим в это выражение формулу (2), а затем преобразуем его. В результате получаем формулу расчёта очередной точки интегральной функции:
y i+1=yi+ h*f (xi,yi) (4).
Из формулы (4) видно, что для расчёта каждой следующей точки интегральной функции необходимо знать значение только одной предыдущей точки. Таким образом, зная начальные условия, можно построить интегральную кривую на заданном промежутке.
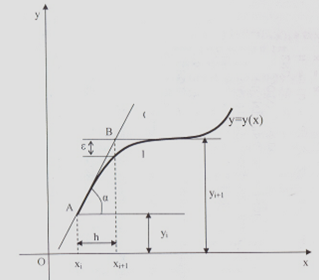
Рисунок 2. Метод Эйлера
Метод Эйлера – один из простейших методов численного решения ОДУ. Но существенным его недостатком является большая погрешность вычислений. На рисунке 2 погрешность вычислений дляi-го шага обозначена ε. С каждым шагом погрешность вычислений увеличивается.
Похожие работы
... . В добавок, собрание геномов и аннотация их модели может быть представлена путем сравнения положения неизвестного гена и его гомологической последовательности из одного организма в другой, который имеет готовые или хорошо аннотированные последовательности генома. Ниже мы опишем методы визуализации, которые используются для отображения синтении на микро и макро уровнях (таб.3). Визуализация ...
... работы со справочной системой работа практикума приостанавливается. 3. Организационно-экономическое обоснование проекта В ходе дипломного проекта был разработан компьютерный лабораторный практикум по курсу «Теория оптимизации и численные методы». В данном разделе рассмотрена экономическая сторона проекта. Рассмотрены следующие вопросы: 1) сетевая модель 2) расчёт ...
... приложением DOS, то имеет недружелюбный интерфейс, однако является достаточно мощным. Кроме вышеназванных пакетов и программ есть еще множество других средств для визуализации инженерных и научных расчетов – от сложных и универсальных, до простых, узкоспециальных. Но для своих специфических применений разработчики отдельных подсистем САПР разрабатывают свои пакеты или покупают и настраивают уже ...
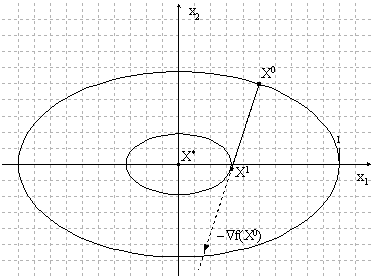
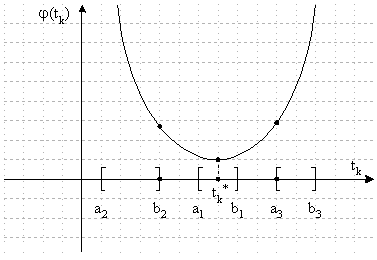
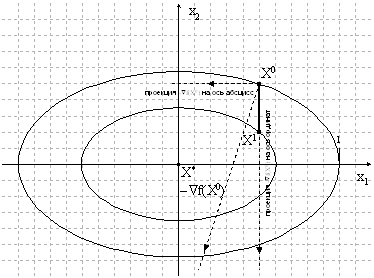
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
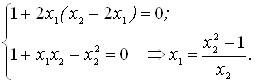
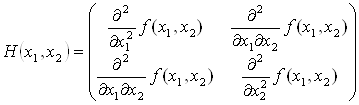

0 комментариев