МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ
ЛУБЕНСЬКА ЗАГАЛЬНООСВІТНЯ ШКОЛА № 3
І-ІІІ СТУПЕНІВ
РЕФЕРАТ
НА ТЕМУ:
ГЕОМЕТРИЧНІ ФІГУРИ НА ПЛОЩИНІ ТА ЇХ ПЛОЩІ
Виконала: учениця 5-Б класу
Німець Євгенія
Лубни 2007
Вступ
Даний реферат охоплює геометричні фігури, що розглядаються в планіметрії - розділі геометрії, в якому вивчають фігури на площині, тобто, так би мовити, у двовимірному світі.
Основними геометричними фігурами на площині є точка і пряма. Я дам їх визначення, як також визначення кута, трикутника, квадрата, чотирикутника, ромба, паралелограма, трапеції, многокутника. Пригадаю, як визначали площі згаданих фігур у часи античності та сучасні методи обчислення площ.
Точка і пряма
Як вже було зазначено, точка і пряма є основними геометричними фігурами на площині. Математично, точкою на площині є об’єкт, два плоскі виміри якого (x і y) прямують до нуля. Тобто, це об’єкт, що має плоскі координати x і y, але не має розмірів, тобто довжини і ширини, тобто це „існуюче ніщо”. Як би я не загострювала кінчик олівця, в надії нанести на площину математичну точку - в мене нічого не вийде. Реально нарисована точка матиме цілком реальні (хай навіть менше 0,1 мм!) розміри по x та по y. Таке визначення точки у математиці було зроблено для спрощення розрахунків.
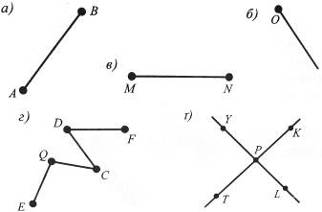
Як правило, всяку геометричну фігуру прийнято вважати складеною з точок. Тому прямою на площині (рис.1) є геометричне місце точок, один з вимірів якого (скажімо довжина) рівний нескінченності, а інший - ширина, прямує до нуля. Для порівняння, відрізок (рис 2), як частина прямої, яка складена з усіх точок прямої, що лежать між двома її точками, має нульову ширину при цілком певній довжині, скажімо 15 см чи 5 м. Півпрямою, або променем (рис.3) називають частину прямої, яка складається з усіх точок цієї прямої, що лежать по один бік від даної на ній точки. Промінь також вважають проведеним у нескінченність в один бік.
![]() Аналогічно попередньому, яким тонким не був би кінчик мого олівця, я не зможу накреслити математичну пряму, відрізок чи промінь - вони матимуть цілком певну ширину.
Аналогічно попередньому, яким тонким не був би кінчик мого олівця, я не зможу накреслити математичну пряму, відрізок чи промінь - вони матимуть цілком певну ширину.
а
рис.1
А В
![]() Рис. 2.
Рис. 2.
 |
Рис.3
Кут
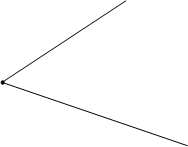 |
Кутом (рис.4) називається фігура, що складається з двох різних півпрямих із спільною початковою точкою, яка називається вершиною кута, а півпрямі - сторонами кута.
Рис.4
Очевидно, що до фігур, зазначених вище, поняття площі незастосовне.
Плоскі геометричні фігури
Чотирикутником взагалі є фігура, складена з чотирьох точок і чотирьох відрізків, які послідовно їх сполучають. Чотирикутник називають опуклим, якщо він розміщений в одній півплощині відносно прямої, яка містить будь-яку його сторону. На рисунках 5 і 6 показано опуклий та неопуклий чотирикутники.
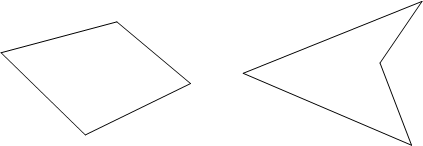
Рис.5 Рис.6
Сторони чотирикутника, що виходять з однієї вершини, називають сусідніми сторонами, а сторони, які не мають спільного кінця - протилежними сторонами.
Прямокутник (рис.7) - це чотирикутник, у якого всі кути прямі.

b
а
Рис. 7.
Як бачимо з рис.7, геометри античності спочатку розбивали прямокутник на квадратики, які були одиницями площі (поняття метр і метр квадратний з’явилось пізніше) і підраховували їх кількість. Тепер використовується формула Sпрям. = аb.
Квадрат - це прямокутник, у якого всі сторони рівні (рис.8).
 |
а
Рис.8
Можна також розбити квадрат на n одиниць площі і знайти їх суму, проте ми користуємося формулою Sквад. = а2.
Паралелограм - це чотирикутник, у якого протилежні сторони паралельні (рис.9).

h
а
Рис.9
Площа паралелограма визначається як добуток його сторони на висоту, проведену до цієї сторони: Sпарал. = аh.
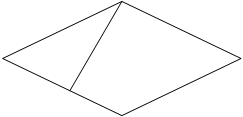
Ромб - це паралелограм, у якого всі сторони рівні (рис.10).
h
а
Рис.10
Площа ромба визначається так само як і площа паралелограма.
Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні (рис.11).
![]()
 b
b
h
а
Рис.11
Площа трапеції дорівнює добутку півсуми її основ на висоту:
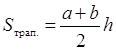
Кругом називається геометричне місце точок площини, що лежать від даної точки на відстані, не більшій за дане число R, яке називається радіусом круга (рис.12).
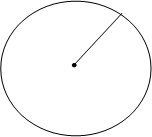
R
Рис.12
Площа круга визначається рівністю: ![]() , де π - число Архімеда, яке рівне відношенню довжини кола до його діаметра, причому вказане відношення є однаковим для будь-якого кола. Не буду зупинятися на виникненні числа π, оскільки багато чого, пов’язаного з його походженням не ясно і дотепер. Доведено ірраціональність числа π. За допомогою комп’ютерів отримані мільйони десяткових знаків цього числа. Перші знаки його такі: π = 3,14159265358…
, де π - число Архімеда, яке рівне відношенню довжини кола до його діаметра, причому вказане відношення є однаковим для будь-якого кола. Не буду зупинятися на виникненні числа π, оскільки багато чого, пов’язаного з його походженням не ясно і дотепер. Доведено ірраціональність числа π. За допомогою комп’ютерів отримані мільйони десяткових знаків цього числа. Перші знаки його такі: π = 3,14159265358…
Трикутником є фігура, що складається з трьох точок і трьох прямих, що їх з’єднують. Розрізняють прямокутні та косокутні трикутники (рис.13, 14)

с
b с b
h
γ
а а
Рис.13 Рис.14
Оскільки прямокутний трикутник можна розглядати як половину прямокутника, то площа прямокутного трикутника рівна 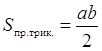 .
.
Взагалі, площа будь-якого трикутника може бути визначена як половина добутку його сторони на висоту, проведену до цієї сторони. За рис.14 запишемо: 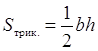 . Існують інші формули для визначення площі трикутника, наприклад
. Існують інші формули для визначення площі трикутника, наприклад 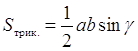 (див. рис.14). Можна також довести формулу Герона для площі трикутника:
(див. рис.14). Можна також довести формулу Герона для площі трикутника:
![]()
де р - півпериметр трикутника, а саме 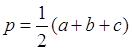 .
.
Якщо плоска фігура зображена в системі координат (x, y), то площа будь-якої з них може бути представлена у вигляді визначеного інтеграла. Дана тема вивчається в 11-му класі середньої школи, тому поки що я не буду її торкатися. За допомогою визначеного інтеграла знаходять площі опуклих і не опуклих криволінійних плоских фігур.
Для площ n-кутників багатьма великими цього світу виведені спеціальні формули, запам’ятати які не завжди легко. Тому я зазвичай, застосовую інший метод обчислення площ багатокутників: всякий n-кутник може бути розбитий на певну кількість простіших фігур, формули площ яких я пам’ятаю.
Похожие работы
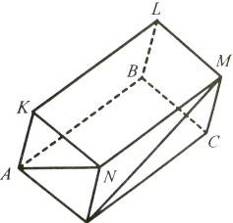
... враховуючи їх невелику кількість у підручниках, посібниках та майже повну відсутність серед добірок завдань контролюючого характеру. 2.2 Загальні методичні рекомендації вивчення елементів стереометрії у курсі геометрії 9 класу 2.2.1 Формування уявлень і понять про стереометричні фігури та деякі їх властивості Формування понять – складний психологічний процес, який починається з утворення ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... сприймали готові образи, що їх дає вчитель, а й самі відтворювали геометричні форми в процесі моделювання, креслення, вирізування, малювання. Тому центральне місце у формуванні геометричних понять займає практика самих школярів. Сприймання простору передбачає сприймання відстані, на якій предмети розміщені від нас і один від одного, напряму, в якому вони перебувають, величини та форми предметів. ...
... в учнів початкових класів геометричних уявлень і понять, та їх підготовку до вивчення систематичного курсу геометрії в 7 – 11 класах. Розділ І. Теоретичні аспекти вивчення геометричного матеріалу в початковій школі І. 1 Загальна характеристика геометричної пропедевтики Як відомо, навчальному предмету «Геометрія», що вивчається в 7 – 11 класах загальноосвітньої школи, передує геометрична ...
0 комментариев