Знайти площу паралелограма, сторони якого дорівнюють 11 см і 16 см, а кут між ними 45°

1. Знайти площу паралелограма, сторони якого дорівнюють 11 см і 16 см, а кут між ними 45°.

2. Знайти площу рівностороннього трикутника, сторона якого дорівнює  см.

Учитель. Посадка закінчується. Провідник перевірить, чи білети справжні. (А він знає свою справу!) Поїзд відбуває до наступної станції.

Станція „Детективна”

Учитель. Знайдено аркуші паперу з розмитими цифрами, знаками, буквами (їх позначено зірочками *). Необхідно їх відновити, інакше поїзд далі не рушить.

ТРИКУТНИКИ

1)     

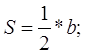
2)     

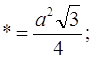
3)     

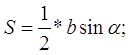
4)     

5)     

 

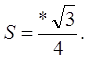
ЧОТИРИКУТНИКИ

1)     

2)     

3)     

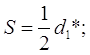
4)     

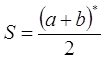
5)     

6)     

7)     

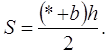
Учитель. Формули ви знаєте, нам дозволено рухатися далі.

Станція „Історична”

Учитель. Сподіваюся, вивчати формул и в XXI ст. декого стимулюватиме той факт, що 4–5 тисяч років тому вавілоняни вміли знаходити площі прямокутника, трапеції, трикутника. Вони користувалися тими самими правилами, що й нині, але сформульованими словесно.

У Стародавній Греції вимірюванням площ цікавився Евклід.

Знайдено деякі рукописи, створені на Русі, зокрема збереглася копія рукопису „О земном верстании, как землю верстать”. Дуже цікаві формули є у ньому. Але є також багато неточностей. Користуючись цими формулами, у 1560 р. побудували храм Василя Бліженого в Москві. Як бачимо, й у ті часи застосовували знання з геометрії на практиці.

А ми продовжимо подорож.

Станція „Практична”

Учитель. Уже недалеко залишилося до нашого міста. Виконана письмова робота (умови завдань записано & картках) буде перепусткою до нього. Задачі 1 і 2 розв'яжіть, виконавши необхідні вимірювання. Перемальовувати малюнки не треба.

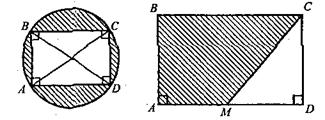1-й варіант

 1. Знайти площі заштрихованих частин фігур.

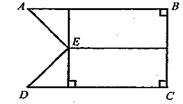2. Знайти площу фігури ABCDE

3. Площа паралелограма дорівнює 96м², а його висоти – 6 м і 8 м. Обчислити периметр паралелограма.

2-й варіант

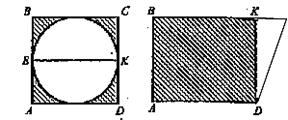1. Знайти площі заштрихованих частин фігурі

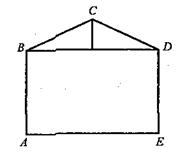
2. Знайти площу фігури ABCDE

3. Діагоналі ромба відносяться як 3:4, а йот сторона дорівнює 25 см. Обчислити площу ромба.

Учитель. Ми потрапили в місто Площеград. Результати подорожі будуть оголошені на наступному уроці. Удома вам треба виконати такі завдання.

1. Скласти дві задачі на обчислення площі та роз в'язати їх.

2. Повторити формули для обчислення площ фігур.

Подорож закінчу словами математика Олексія Миколайовича Крилова: „Рано чи пізно будь-яка правильна математична ідея знаходить застосування в тій чи іншій справі. Завтра математика стане ще могутнішою, ще важливішою і потрібнішою для людей, ніж сьогодні”[17, 37].

Висновки

Аналіз результатів дослідження дозволяє зробити такі висновки.

1.  В умовах перебудови суспільства та всіх його сфер виникає необхідність перебудови навчально-виховного процесу в школі. Рівень навченості, розвитку, вихованості та пристосованості підлітків 7-9-х класів до суспільних умов можна суттєво підвищити, якщо на уроках математики поєднати їх навчальну діяльність з ігровою. Таке поєднання забезпечує задоволення головних вікових потреб підлітків у спілкуванні з однолітками та самоутвердженні і тому сприяє підвищенню рівня успішності у навчанні.

2.  Найважливішими умовами організації ігрової діяльності на уроках математики учнів 7-9-х класів з метою покращення якості та успішності навчання, виховання та розвитку підлітків є вибір доцільної дидактичної гри, дотримання вимог до змісту та проведення дидактичних ігор, визначення місця і ролі їх у в системі інших видів навчально-пізнавальної діяльності підлітків, вибір доцільних способів керівництва грою.

3.  Використання дидактичних ігор в процесі вивчення геометрії в 7-9-х класах підвищує успішність та якість навчання.

Вміле поєднання індивідуальних, групових, мережевих та колективних форм навчальної діяльності у процесі дидактичних ігор на уроках геометрії в 7-9-х класах допомагає учням долати соціально-психологічні та фізіологічні бар'єри, які виникають під час вивчення математики.

4.  Уроки математики в 7-9-х класах, організовані з використанням дидактичних ігор, під час яких учні виступають в ролі консультантів, виконавців, аудиторів тощо, дають змогу виховувати в учнів активність, бажання вивчати математику, розвивають їх пізнавальні інтереси.

Список використаних джерел

1.   Букатова В.М., Ершова А.П. Я иду на урок: Хрестоматия игровых прийомов обучения: Книга для учителя.–М.: Первое сентября,–2000.–224с.

2.   Грамбовська Л. Коригування методичної системи навчання геометрії основної школи.// Математика в школі. – 2006. №5.–С.56-60.

3.   Довгаль О. Площі многокутників (Урок подорож у 9 класі)// Математика в школі– 2006.–№15.–С.22–24.

4.   Зимний А.И. Элементы игры на уроках// Математика в школе. – 1977.–№6.–С.24–29.

5.   Зозуля О. Геометричні фігури (Урок-гра у 6 класі). // Математика.– 2007.– №5.–С.22–24.

6.   Коваленко В.Г. Дидактические игры на уроках математики. – М.: Просвещение, 1990.–91с.

7.   Козира В.М. Технологія уроку з математики. –Тернопіль: Астон, 2002.–52с.

8.   Латышев В. М. Псохолого-педагогические проблемы развития мышления личности учащихся в условиях информатизации образования // Информатика и образование. –2003. –№6.–С.32–42.

9.   Мартинюк Ю.И. От игры к знаниям. // Математика в школе.– 2006.–№9.–С.80–84.

10.  Микитин О.В. Використання дидактичних ігор на уроках математики.// Математика.–2004.–№38.–С.37–45.

11.  Перова М.Н. Дидактические игры и упражнения по математике. - М.: Просвещение, 1996.–84с.

12.  Погорєлов О.В. Геометрія: Підручник для 7-11 кл. серед. шк.–К. Освіта, 1993.–351с.

13.    Психолого-педагогические особенности проведения дидактических игр. Под.ред. Акшиной А., Акшиной Т., Жарковой Т. М., 1990.–147с.

14.  Романенко А.О. Математика і комп’ютерні технології // Комп’тер у школі та сім’ї. –2001. –№1.–С.41–44.

15.  Слєпкань З.І. Методика навчання математики.–К.: Зодіак– Еко, 2000.–512с.

16.  Слепкань З.И. Психолого-педагогические основы обучения математики: Метод. пособие. –К.: Рад. школа,–1983.–192с.

17.  Сухарева Л.С. Дидактичні ігри на уроках математики. 7-9 класи.–Харків: Основа, –2006.–144с.

18.  Тополя Л.В. Дидактичні ігри, їх види, цільове призначення і функції в навчальному процесі //Дидактика математики: проблеми дослідження. – Міжнародний збірник наукових робіт. –Донецьк: ТЕАН, 2001.– Вип.16.– С.167–173.

19.  Чилинрова Л., Спиридонова Б. Играя, учимся математике. М., 1993.–с.218.

20.  Чудовский А.Н., Сомова Л.А. Проверьте свои знания по геометрии: Кн. для учащихся 9 и 10 кл. сред. шк. –М.: Просвещение, 1987.–96с.

21.  Эльконин Д.Б. Психология игры - М.: Высшая школа, 1978.–312с.

Додаток А

Етапи підготовки і проведення дидактичної гри

 

Підготовка і проведення дидактичної гри включає чотири етапи:

1.    Орієнтація: учитель задає тему, дає характеристику гри, загальний огляд її ходу й правил.

2.    Підготовка до проведення: ознайомлення зі сценарієм, розподіл ролей, підготовка до їхнього виконання, забезпечення процедур керування грою.

3.    Проведення гри: учитель стежить за ходом гри, контролює послідовність дій, надає необхідну допомогу, фіксує результати.

4.    Обговорення гри: дається характеристика виконання дій, їхнього сприйняття учасниками, аналізуються позитивні й негативні сторони ходу гри, що виникли труднощі, обговорюються можливі шляхи вдосконалювання гри, у тому числі зміни її правил.

Додаток Б

Вимоги до організації дидактичних ігор

 

Запровадження дидактичної гри у навчальний процес вимагає дотримання певних правил:

1.    Вільне й добровільне включення учнів у гру: не нав'язування гри, а залучення в неї учнів.

2.    Учні повинні добре розуміти сутність і зміст гри, її правила, ідею кожної ігрової ролі.

3.    Сутність ігрових дій повинна збігатися із сутністю і змістом поводження в реальних ситуаціях для того, щоб основний зміст ігрових дій переносився в реальну життєдіяльність.

4.    У грі повинні керуватися прийнятими в суспільстві нормами моральності, заснованими на гуманізмі, загальнолюдських цінностях.

5.    У грі не повинна принижуватися гідність її учасників, зокрема тих, що програли.

6.    Гра повинна позитивно впливати на розвиток емоційно-вольової, інтелектуальної й раціонально-фізичної сфер її учасників.

7.     Гру потрібно організовувати й направляти, при необхідності стримувати, але не придушувати, забезпечувати кожному учасникові можливість прояву ініціативи.

8.    У підлітковому й особливо в старших класах необхідно спонукати учнів до аналізу проведеної гри, до зіставлення імітації з відповідною областю реального життя, надавати допомогу у встановленні зв'язку гри зі змістом практичної життєвої діяльності або зі змістом навчального курсу.

9.    Ігри не повинні бути зайво виховними й зайво дидактичними: їхній зміст не повинен бути нав'язливо повчальним і не повинне містити занадто багато інформації.

Додаток В

Принципи, на яких ґрунтується дидактична гра

 

Принципи, на яких ґрунтується дидактична гра, мають узгоджуватися з основними принципами навчання в школі.

Науковці відносить до цих принципів:

–принцип розвивального навчання;

–принцип навчання, що виховує;

–принцип доступності навчання;

–принцип системності й послідовності;

–принцип свідомості й активності дітей у засвоєнні й застосуванні знань;

–принцип індивідуального підходу до дітей.

До перерахованих вище принципів У.І Логинова, розглядаючи навчання як засіб всебічного розвитку особистості, додає ще принцип міцності знань.

Додаток Г

УРОК – СЛІДСТВО У 9 КЛАСІ

Тема: Чотирикутники.

Мета уроку: закріплення та систематизація знань учнів з теми; активізація діяльності учнів у ході навчання; підвищення інтересу учнів до вивчення предмета.

Обладнання і оформлення уроку: картки-креслення завдань; аудіо-магнітофон із записом музики до телефільму «Пригоди Шерлока Холмса і доктора Ватсона».

Форма проведення уроку: гра „Слідство ведуть знавці геометрії”.

Звучить музика. Вчитель зачитує план слідчо-пошукових заходів.

Етапи уроку (план слідчо-пошукових заходів)

•   Формування слідчих груп.

•   Встановлення осіб, укладання орієнтирів.

•   Складання фотороботів.

•   Експертиза речових доказів.

•   Винесення звинувачення та його доведення.

•   Підбиття підсумків слідчо-пошукових заходів.

•   Повідомлення домашнього завдання.

ХІД УРОКУ