Навигация
Евклидова плоскость R2, на которой существует базис, в котором скалярное произведение любых двух векторов этой плоскости записывается в виде
1. Евклидова плоскость R2, на которой существует базис, в котором скалярное произведение любых двух векторов этой плоскости записывается в виде
![]() , где
, где ![]() .
.
Например, евклидова плоскость - плоскость ![]() . Для векторов этой плоскости
. Для векторов этой плоскости ![]() ,
, ![]() .
.
Тогда,
![]()
2. Псевдоевклидова плоскость1R2, на которой существует базис, в котором скалярное произведение любых двух векторов этой плоскости записывается в виде ![]() , где
, где ![]() .
.
Например, евклидовой плоскостью является плоскость ![]() . Для векторов этой плоскости
. Для векторов этой плоскости![]() ,
, ![]() . Получим,
. Получим,
![]()
3. Полуевклидова плоскость![]() , на которой существует базис, в котором скалярное произведение любых двух векторов этой плоскости принимает вид
, на которой существует базис, в котором скалярное произведение любых двух векторов этой плоскости принимает вид ![]() , где
, где ![]() .
.
Например, полуоевклидова плоскость - плоскость ![]() . Для векторов этой плоскости
. Для векторов этой плоскости
![]() ,
, ![]() .
.
Тогда получим,
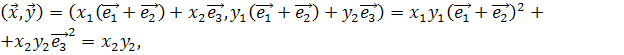 т.к.
т.к. ![]()
Псевдоевклидова плоскость по своим аффинным свойствам не отличается от евклидовой, однако метрические свойства этих плоскостей существенно различаются. Это видно, хотя бы на примере окружности, которую на псевдоевклидовой плоскости определим как совокупность всех точек, удаленных на одно и то же псевдоевклидово расстояние r от данной точки – центра.
Если центр совпадает с началом координат О(0,0), то по определению уравнение окружности имеет вид
![]() .
.
Радиус окружности может быть вещественным (r=a), тогда ![]() .
.
Если радиус окружности мнимый, т.е. r=ia, то ![]() . В случае, когда радиус r=0, имеем
. В случае, когда радиус r=0, имеем ![]() .
.
Таким образом на ![]() существует три вида окружностей. На аффинной плоскости они представляют собой пару пересекающихся прямых – окружность нулевого радиуса – и две сопряженные гиперболы, для которых указанные прямые являются асимптотами. (Рис. 1.2)
существует три вида окружностей. На аффинной плоскости они представляют собой пару пересекающихся прямых – окружность нулевого радиуса – и две сопряженные гиперболы, для которых указанные прямые являются асимптотами. (Рис. 1.2)
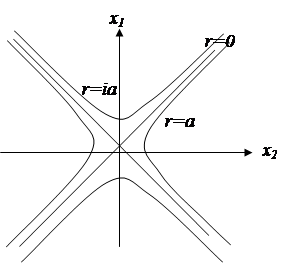 | |||
| |||
В пространстве 1R4 существует три типа 3-плоскостей.
1. Евклидова 3-плоскость R3, на которой существует базис, в котором скалярное произведение принимает вид:
![]() .
.
Например, евклидовой 3-плоскостью является плоскость ![]() Для векторов этой 3-плоскости
Для векторов этой 3-плоскости ![]() ,
, ![]() Тогда получим,
Тогда получим, ![]() ,
,![]() )=
)=![]()
2. Плоскость 1R3, на которой существует базис, в котором скалярное произведение принимает вид:
![]() .
.
Например, плоскостью 1R3 является плоскость ![]() Для векторов этой 3-плоскости
Для векторов этой 3-плоскости ![]() ,
, ![]() Получаем,
Получаем,
![]() ,
,![]() )=
)=![]()
3. Плоскость ![]() , на которой существует базис, в котором скалярное произведение принимает вид:
, на которой существует базис, в котором скалярное произведение принимает вид: ![]() .
.
Например, плоскостью ![]() является плоскость
является плоскость ![]() Для векторов этой 3-плоскости
Для векторов этой 3-плоскости ![]() ,
, ![]() .
.
Получим:
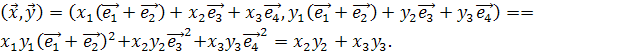
Поскольку каждая 3-плоскость ортогональна некоторой прямой, то существует только 3 типа 3-плоскостей.
Определение 1.3. Ортогональным дополнением к векторному пространству LÌ1R4 называется векторное пространство, образованное всеми векторами, ортогональными к пространству L.
Пример. Найдем множество векторов, ортогональных к вектору ![]() . Если вектор
. Если вектор ![]() ортогонален
ортогонален ![]() , то
, то ![]() . Отсюда,
. Отсюда,
![]() =
=![]() .
.
Таким образом, ортогональным дополнением к вектору ![]() является множество векторов
является множество векторов ![]() . Эти векторы определяют 3-плоскость
. Эти векторы определяют 3-плоскость ![]() которое является 3-плоскостью вида 1R3. Следовательно, R1^1R3. Это означает, что к прямой R1 ортогональной является 3-плоскость типа1R3. Верно и обратное.
которое является 3-плоскостью вида 1R3. Следовательно, R1^1R3. Это означает, что к прямой R1 ортогональной является 3-плоскость типа1R3. Верно и обратное.
Аналогично найдем множество векторов ортогональных к вектору![]() . Если вектор
. Если вектор ![]() ортогонален
ортогонален ![]() , то
, то ![]() . Отсюда,
. Отсюда,
![]() =
=![]() .
.
Множество векторов, ортогональных вектору ![]() , имеет вид
, имеет вид ![]() и определяет 3-плоскость
и определяет 3-плоскость ![]() которое является 3-плосткостью вида R3. Следовательно, 1R1^R3. Это означает, что к прямой 1R3 ортогональной является 3-плоскость типа R3. Верно и обратное.
которое является 3-плосткостью вида R3. Следовательно, 1R1^R3. Это означает, что к прямой 1R3 ортогональной является 3-плоскость типа R3. Верно и обратное.
Рассмотрим вектор (![]() ) и найдем множество векторов ортогональных к данному вектору. Если вектор
) и найдем множество векторов ортогональных к данному вектору. Если вектор ![]() ортогонален (
ортогонален (![]() ), то
), то ![]() .
.
Получаем, что
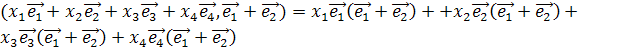 =
=![]() .
.
Отсюда, ![]() , а
, а ![]() — произвольные.
— произвольные. ![]() - это множество векторов, ортогональных вектору (
- это множество векторов, ортогональных вектору (![]() ) и определяет 3-плоскость
) и определяет 3-плоскость ![]() которое является 3-плосткостью вида
которое является 3-плосткостью вида ![]() . Значит,
. Значит, ![]() ^
^![]() . Это означает, что к прямой
. Это означает, что к прямой ![]() ортогональной является 3-плоскость типа
ортогональной является 3-плоскость типа ![]() . Верно и обратное.
. Верно и обратное.
Заметим, что ![]() Ì
Ì![]() .
.
Найдем множество векторов, ортогональных к векторам ![]() . Если вектор
. Если вектор ![]() ортогонален
ортогонален ![]() , то
, то ![]() Отсюда,
Отсюда,
![]() Û
Û ![]()
Таким образом, ортогональным дополнением к векторам ![]() является множество векторов
является множество векторов ![]() . Эти векторы определяют 2-плоскость
. Эти векторы определяют 2-плоскость ![]() которая является 2-плосткостью вида 1R2. Следовательно, R2 ^1R2 (к двумерной плоскости R2 ортогональной является плоскость вида 1R2).
которая является 2-плосткостью вида 1R2. Следовательно, R2 ^1R2 (к двумерной плоскости R2 ортогональной является плоскость вида 1R2).
Найдем множество векторов, ортогональных к векторам ![]() . Если вектор
. Если вектор ![]() ортогонален
ортогонален ![]() , то
, то ![]() Отсюда,
Отсюда,![]()
![]() Û
Û ![]()
Таким образом, ортогональным дополнением к векторам ![]() является множество векторов
является множество векторов ![]() . Эти векторы определяют 2-плоскость
. Эти векторы определяют 2-плоскость ![]() которое является 2-плосткостью вида R2, Следовательно, R2 ^1R2 (к двумерной плоскости R2 ортогональной является плоскость вида 1R2). Верно и обратное.
которое является 2-плосткостью вида R2, Следовательно, R2 ^1R2 (к двумерной плоскости R2 ортогональной является плоскость вида 1R2). Верно и обратное.
![]() Найдем множество векторов, ортогональных к векторам
Найдем множество векторов, ортогональных к векторам![]() Если вектор
Если вектор ![]() ортогонален
ортогонален ![]() , то
, то
![]()
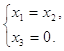 Отсюда,
Отсюда,
![]() Û
Û
Û![]()
Таким образом, ортогональным дополнением к векторам ![]() является множество векторов
является множество векторов ![]() . Эти векторы определяют 2-плоскость
. Эти векторы определяют 2-плоскость ![]() которая является 2-плосткостью вида
которая является 2-плосткостью вида ![]() . Следовательно,
. Следовательно, ![]() ^
^![]() .
.
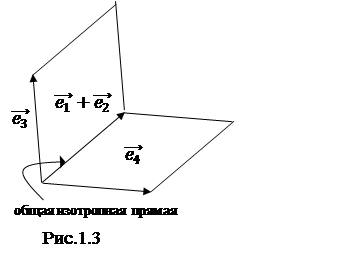 |
Таким образом, получена теорема.
Теорема 1.1. В пространстве 1R4 существуют следующие типы прямых, плоскостей и 3-плоскостей:
- прямые: R1, 1R1,![]() .
.
- 2-плоскости: R2, 1R2,![]() .
.
- 3-плоскости: R3, 1R3,![]() .
.
§2. Кривые в пространстве 1R4
В пространстве 1R4 выберем базис
![]() ,
,
где![]() Точка MÎ1R4, имеющая в репере R координаты (
Точка MÎ1R4, имеющая в репере R координаты (![]() ): M(
): M(![]() )R.
)R.
Определение 2.1. Кривой в пространстве 1R4 называется множество точек этого пространства, координаты которых задаются уравнениями:
![]() (6)
(6)
Или в векторном виде ![]() . (7)
. (7)
Определение 2.2. Функция, имеющая непрерывные производные до k-го порядка включительно на отрезке [a,b], называется k раз дифференцируемой функцией на этом отрезке.
Определение 2.3. Кривая g называется дифференцируемой класса Сk, если функции (6), задающие параметрические уравнения, являются k раз дифференцируемыми функциями.
Пусть кривая g является кривой класса C3. Рассмотрим на дифференцируемой кривой g вектора:
![]()
![]() .
.
Определение 2.4. Точка M, принадлежащая кривой g, называется неособой, если в этой точке вектора ![]()
![]() ,
, ![]() линейно независимы. В противном случае точка M кривой g называется особой.
линейно независимы. В противном случае точка M кривой g называется особой.
Определение 2.5. Прямая ![]() называется касательной к кривой в точке M, 2-плоскость
называется касательной к кривой в точке M, 2-плоскость ![]() называется соприкасающейся плоскостью кривой g, 3-плоскость
называется соприкасающейся плоскостью кривой g, 3-плоскость ![]() называется соприкасающейся 3-плоскостью кривой g в точке M.
называется соприкасающейся 3-плоскостью кривой g в точке M.
Очевидно, ![]() Ì
Ì![]() Ì
Ì![]() .
.
Теорема 2.1. Кривая g имеет в каждой точке касательную и притом единственную.
Если r=r(t) - векторное уравнение кривой, то касательная в точке Р, соответствующей значению параметра t, имеет направление вектора r'(t).
Теорема 2.2. Кривая g имеет в каждой точке соприкасающуюся плоскость. При этом соприкасающаяся плоскость либо единственная, либо любая плоскость, содержащая касательную к кривой, является соприкасающейся.
Если r=r(t) – уравнение кривой g, то соприкасающаяся плоскость в точке, соответствующей значению параметра t, параллельна векторам r'(t) и r''(t).
Теорема 2.3. Задание касательной, соприкасающейся плоскости и соприкасающейся 3-плоскости корректно, т.е. не зависит от параметризации кривой.
Для доказательства достаточно перейти к новому параметру и сравнить направляющие вектора.
![]()
![]()
![]()
![]()
![]()
![]()
Определение 2.5. Соприкасающийся флаг – это совокупность, состоящая из точки кривой, касательной к кривой в этой точке, соприкасающейся 2-плоскости к кривой в этой точке и соприкасающейся 3-плоскости к кривой в этой точке. [M, ![]() ], M Ì
], M Ì![]() Ì
Ì![]() Ì
Ì![]() .
.
Соприкасающийся флаг может быть следующих видов.
10. {M, R1, R2, R3}. Например, ![]()
20. {M, R1, 1R2, 1R3}. Например, ![]()
30. {M, R1, ![]() , 1R3}. Например,
, 1R3}. Например, ![]()
40. {M, R1, ![]() ,
, ![]() }. Например,
}. Например, ![]()
50. {M, 1R1, 1R2, 1R3}. Например, ![]()
60. {M, ![]() ,
, ![]() , 1R3}. Например,
, 1R3}. Например, ![]()
70. {M, ![]() ,
, ![]() ,
, ![]() }. Например,
}. Например, ![]()
80. {M, R1, R2, 1R3}. Например, ![]()
90. {M, R1, R2, ![]() }. Например,
}. Например, ![]()
100. {M, ![]() , 1R2, 1R3}. Например,
, 1R2, 1R3}. Например, ![]()
Более подробно в своей дипломной работе я рассмотрю кривые, имеющие соприкасающийся флаг вида 20.
Рассмотрим кривую g с соприкасающимся флагом 20.
Построим в произвольной точке M кривой g канонический репер {M, e1, e2, e3, e4}.
Введем на кривой g естественную параметризацию s следующим образом:
![]() (8)
(8)
Теорема 2.4. Для кривой g: ![]() , заданной в естественной параметризации, получим
, заданной в естественной параметризации, получим
![]()
![]() (9)
(9)
Доказательство.
![]() .
.
Из (8) следует ![]() . Значит,
. Значит,![]() и, следовательно,
и, следовательно,
![]() ,
, ![]() . (10)
. (10)
Дифференцируем равенство (10): ![]() Отсюда,
Отсюда, ![]()
Ч.т.д.
Вектор ![]() направлен по касательной
направлен по касательной ![]() в точке М:
в точке М: ![]() . Вектор
. Вектор ![]() выберем в соприкасающейся плоскости
выберем в соприкасающейся плоскости ![]() перпендикулярно
перпендикулярно ![]() :
:
Условие перпендикулярности к ![]() в соприкасающейся плоскости:
в соприкасающейся плоскости:![]() Отсюда:
Отсюда: ![]() .
.
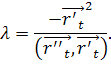
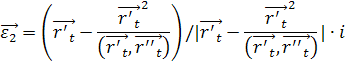
Вектор ![]() выберем в соприкасающейся 3-плоскости
выберем в соприкасающейся 3-плоскости ![]() перпендикулярно векторам
перпендикулярно векторам ![]() и
и ![]() .
.
![]() (11)
(11)
Найти ![]() и
и ![]() можно используя условия ортогональности:
можно используя условия ортогональности:
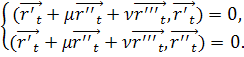
Подставив ![]() и
и ![]() в формулу (8) получим вектор
в формулу (8) получим вектор ![]() .
.
Вектор ![]() выберем в 1R4 перпендикулярно
выберем в 1R4 перпендикулярно ![]() ,
,![]() ,
,![]() .
.
В нашем случае векторы ![]() ,
,![]() ,
,![]() - векторы действительной длины, а вектор
- векторы действительной длины, а вектор ![]() - вектор мнимой длины.
- вектор мнимой длины.
Пусть кривая g задана в естественной параметризации. Вектора ![]() ,
,![]() ,
, ![]() , канонического репера будут заданы тоже с помощью параметра s.
, канонического репера будут заданы тоже с помощью параметра s.
Рассмотрим векторы ![]() ,
,![]() ,
, ![]() . Эти векторы можно будет разложить по базису
. Эти векторы можно будет разложить по базису ![]() ,
,![]() ,
, ![]() :
:
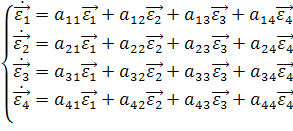 (12)
(12)
Теорема 2.5. Производная вектора постоянной длины перпендикулярна этому вектору.
Доказательство.
Пусть ![]()
![]()
Ч.т.д.
Из теоремы 2.5. следует, что ![]() .
.
Домножим первое уравнение (12) скалярно на ![]() . Получим
. Получим ![]() . Аналогично,
. Аналогично,
![]() . (13)
. (13)
Домножим первое уравнение (12) скалярно на ![]() , второе на
, второе на ![]() , затем сложим их. (
, затем сложим их. (![]() ,
,![]() )+(
)+(![]() ,
,![]() )=
)=![]() +
+![]() . Выражение
. Выражение ![]() =0.
=0.
Отсюда, ![]() =
= ![]() .
.
Аналогично, ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
,![]() =
=![]() .
.
Выберем ![]() ,
, ![]() . При этом
. При этом ![]() имеет действительную длину. Тогда
имеет действительную длину. Тогда
![]() (14)
(14)
Исходя из (12) и (14), получим ![]() =
=![]() . Следовательно,
. Следовательно, ![]() =
=![]() =0.
=0.
![]() .
.
Значит, ![]() раскладывается по векторам
раскладывается по векторам ![]() ,
,![]() ,
,![]() , задающим
, задающим ![]() . Значит,
. Значит, ![]() =0, а следовательно
=0, а следовательно ![]() =0.
=0.
![]() . Пусть
. Пусть ![]() k1(s).
k1(s).
Деривационные формулы запишутся в виде:
|
|
|
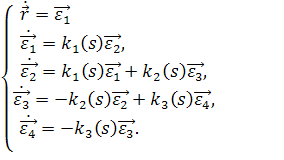
§3. Понятие о линейчатых и развертывающихся поверхностях
Поверхность, представляющая собой геометрическое место прямых линий, называется линейчатой. Точнее линейчатую поверхность мы будем строить следующим образом.
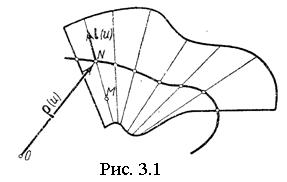
Возьмем какую-нибудь кривую в пространстве; пусть r — ее текущий радиус-вектор, а u - параметр, к которому она отнесена, r = r(u). Эту кривую мы будем называть направляющей. В каждой точке этой кривой зададим единичный вектор, который будет являться, таким образом, также функцией параметра u вдоль кривой, l=l(u).
|
В таком случае радиус-вектор произвольной точки М на произвольной образующей, определяемой значением ![]() , можно записать в виде
, можно записать в виде
![]()
![]() r(u),
r(u), ![]() ;
;
действительно, вектор NM коллинеарен единичному вектору ![]() и потому отличается от него лишь скалярным множителем, равным длине NM с соответствующим знаком, т. е. множителем v.
и потому отличается от него лишь скалярным множителем, равным длине NM с соответствующим знаком, т. е. множителем v.
Итак, окончательно ![]() .
.
В результате радиус-вектор произвольной точки М на произвольной образующей выразился как функция двух независимых параметров u, v. Мы получили, таким образом, параметрическое представление линейчатой поверхности, именно той, которая образована прямыми (образующими) построенного нами однопараметрического семейства прямых.
Фиксируя в этом уравнении u и меняя v, мы движемся, очевидно, по образующей, отвечающей данному значению u. Следовательно, семейством координатных линий v у нас будут служить образующие. Если же фиксировать v и менять u, то мы идем по образующим «параллельно» направляющей линии в том смысле, что расстояние NM = v остается постоянным.
Таким образом, координатные линии u образуют семейство линий, «параллельных» направляющей линии, которая сама также входит в это семейство и отвечает случаю, когда v фиксировано на значении 0.
Заметим, что направляющая линия геометрически ничем на заданной линейчатой поверхности не выделяется. В качестве направляющей может быть взята любая кривая на линейчатой поверхности, последовательно пересекающаяся с ее образующими; произвол этот отразится только на выборе параметров u, v на поверхности.
Вычислим теперь частные производные радиус-вектора по параметрам. Очевидно,
![]() (16)
(16)
Составим векторное произведение этих векторов, направленное, как мы знаем, по нормали к поверхности:
![]() (17)
(17)
Исследуем поведение нормали к линейчатой поверхности, когда точка движется по поверхности вдоль какой-нибудь образующей, т. е. когда мы меняем v при фиксированном u. Так как ![]() , l являются функциями только u, то векторные произведения
, l являются функциями только u, то векторные произведения ![]() и
и ![]() остаются постоянными, и правая часть (17) может меняться лишь вследствие изменения коэффициента v.
остаются постоянными, и правая часть (17) может меняться лишь вследствие изменения коэффициента v.
Здесь мы будем различать два случая, общий и специальный.
Общий случай: векторные произведения ![]() и
и ![]() не коллинеарны. В этом случае при движении вдоль образующей, т. е. при изменении v, первое слагаемое в правой части (17) постоянно, второе же, ему не параллельное, изменяется пропорционально v. В результате вся правая часть представляет собой вектор, направление которого меняется вместе с v.
не коллинеарны. В этом случае при движении вдоль образующей, т. е. при изменении v, первое слагаемое в правой части (17) постоянно, второе же, ему не параллельное, изменяется пропорционально v. В результате вся правая часть представляет собой вектор, направление которого меняется вместе с v.
|
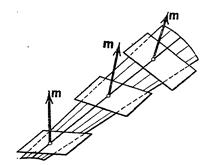
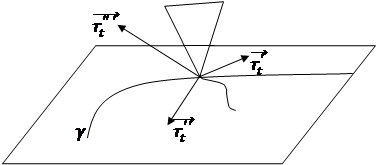
Следовательно, вдоль образующей направление нормали к поверхности меняется от точки к точке. Очевидно, что касательная плоскость в какой-нибудь точке на данной образующей проходит через эту образующую (так как образующая является своей собственной касательной). Поэтому при движении точки касания вдоль образующей касательная плоскость, все время проходя через образующую, вращается около нее. В этом случае линейчатая поверхность называется косой (Рис. 3.2).
Специальный случай: векторные произведения ![]() и
и ![]() коллинеарны.
коллинеарны.
|
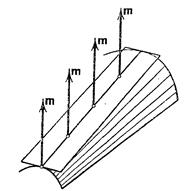
В этом случае оба слагаемых в правой части (17) параллельны друг другу (а следовательно, и своей сумме) при любом значении v. Таким образом, все нормали вдоль данной образующей параллельны между собой, так как они параллельны векторам ![]() и
и ![]() . Когда точка касания движется вдоль образующей, то касательная плоскость проходит все время через образующую; и так как касательная плоскость должна, кроме того, оставаться перпендикулярной к неизменному направлению нормали, то она не может вращаться около образующей и остается неподвижной.
. Когда точка касания движется вдоль образующей, то касательная плоскость проходит все время через образующую; и так как касательная плоскость должна, кроме того, оставаться перпендикулярной к неизменному направлению нормали, то она не может вращаться около образующей и остается неподвижной.
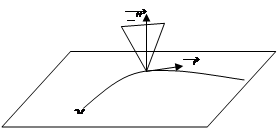
Итак, в рассматриваемом случае касательные плоскости к поверхности в точках, расположенных на одной и той же образующей, совпадают между собой. Такую линейчатую поверхность мы будем называть развертывающейся поверхностью (Рис. 3.3).
Обратно, если мы имеем развертывающуюся поверхность, т. е. касательная плоскость для всех точек образующей одна и та же, и нормали вдоль образующей параллельны, то направление вектора (17) не зависит от значения v, что возможно лишь в случае
![]() ||
|| ![]() (18)
(18)
Таким образом, условие (18) необходимо и достаточно для того, чтобы линейчатая поверхность оказалась развертывающейся. Этому условию можно придать более простую форму.
Общее направление двух векторных произведений будет ортогональным ко всем их множителям, т. е. к векторам ![]() ,
, ![]() , которые, таким образом, оказываются компланарными (параллельными одной плоскости).
, которые, таким образом, оказываются компланарными (параллельными одной плоскости).
Легко видеть, что это условие и достаточно. Итак, условие (18) может быть переписано в эквивалентном виде ![]() ,
, ![]() компланарны, т.е.
компланарны, т.е.
(![]() ,
, ![]() = 0. (19).
= 0. (19).
Это условие наложено, как мы видим, на вектор-функции ![]() (радиус-вектор направляющей кривой) и
(радиус-вектор направляющей кривой) и ![]() , (единичный вектор на образующей). Плоскость векторов (19) будет параллельна векторам (16) при любом значении v, т. е. параллельна касательной плоскости, проходящей через соответствующую образующую.
, (единичный вектор на образующей). Плоскость векторов (19) будет параллельна векторам (16) при любом значении v, т. е. параллельна касательной плоскости, проходящей через соответствующую образующую.
§4. Торсы в пространстве 1R4
Рассмотрим кривую
![]() (20) в пространстве 1R4.
(20) в пространстве 1R4.
Определение 4.1. Торсом в пространстве 1R4, определенном кривой g называется поверхность, образованная всеми касательными к этой кривой.
Сама кривая g называется ребром возврата этого торса. Каждая касательная к ребру возврата называется прямолинейной образующей торса.
Уравнение торса
|

![]()
![]() (21)
(21)
(21) – уравнение торса, определяемого ребром возврата ![]() .
.
На ребре возврата ![]() выберем естественную параметризацию. Пусть t=t(s), тогда
выберем естественную параметризацию. Пусть t=t(s), тогда ![]() и s=i
и s=i![]() .
.
Свойства естественной параметризации:
1. ![]() ;
;
![]() . Значит
. Значит ![]()
2. ![]() ;
;
(![]() )=
)=![]() =1
=1![]() (
(![]() )+ (
)+ (![]() )=0;
)=0;
2(![]() )=0
)=0![]() (
(![]() )=0
)=0 ![]()
Исследуем торс (21) в пространстве 1R4, обозначив при этом t = u, t = v.
Тогда уравнение торса (21) запишется в виде: ![]() . (22)
. (22)
По теореме о развертывающейся линейчатой поверхности векторы ![]() должны лежать в одной плоскости. Очевидно, что данные вектора лежат в одной плоскости, т.к. два из них одинаковы. Следовательно, торс развертывающаяся линейчатая поверхность, а значит, касательная плоскость к торсу в любой его точке не зависит от параметра v, что легко доказать. Действительно из формул (22) получим:
должны лежать в одной плоскости. Очевидно, что данные вектора лежат в одной плоскости, т.к. два из них одинаковы. Следовательно, торс развертывающаяся линейчатая поверхность, а значит, касательная плоскость к торсу в любой его точке не зависит от параметра v, что легко доказать. Действительно из формул (22) получим:
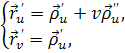 Þ
Þ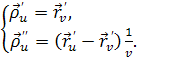
Это означает, что базисы {![]() } и {
} и {![]() } выражаются друг через друга. Из этого следует, что
} выражаются друг через друга. Из этого следует, что
![]() (23),
(23),
при любом параметре v, значит касательная плоскость к торсу одна и та же вдоль образующей. Известно, что соприкасающаяся плоскость к кривой g в точке M определяется векторами ![]() . Таким образом, исходя из формулы (23) получим, что соприкасающаяся плоскость ребра возврата g - есть касательная плоскость к торсу.
. Таким образом, исходя из формулы (23) получим, что соприкасающаяся плоскость ребра возврата g - есть касательная плоскость к торсу.
Рассмотрим торс пространства 1R4, порожденной кривой ![]() определяемый уравнением (23). Введем координатные линии на поверхности торса: u-линии (v=c) и v-линии (u=c). Найдем скалярное произведение векторов
определяемый уравнением (23). Введем координатные линии на поверхности торса: u-линии (v=c) и v-линии (u=c). Найдем скалярное произведение векторов ![]()
![]() (24)
(24)
В общем случае относительно величин ![]() и
и ![]() ничего сказать нельзя. Поэтому будем делать предположение относительно кривой g. Предположим, что касательный вектор к кривой g во всех точках является вектором действительной длины. На ребре возврата g выбираем естественную параметризацию. Пусть u=u(s), тогда
ничего сказать нельзя. Поэтому будем делать предположение относительно кривой g. Предположим, что касательный вектор к кривой g во всех точках является вектором действительной длины. На ребре возврата g выбираем естественную параметризацию. Пусть u=u(s), тогда ![]() и
и ![]() Параметр s обозначим через u, получим
Параметр s обозначим через u, получим ![]() , т.е. вектор
, т.е. вектор ![]() имеет постоянную длину, тогда поскольку
имеет постоянную длину, тогда поскольку ![]() , из (24) следует, что
, из (24) следует, что ![]() , а значит координатные линии на торсе в такой системе координат не ортогональны. Перейдем к новым координатам U и V так, чтобы координатные линии были ортогональны, причем заметим, чтоv-линии – это прямолинейные образующие торса. При переходе к новым координатам потребуем, чтобы семейство v-линий осталось прежним, а u-линии изменились и стали перпендикулярны v-линиям. Таким образом, перед нами стоит задача отыскания ортогональных траекторий к прямолинейным образующим торса.
, а значит координатные линии на торсе в такой системе координат не ортогональны. Перейдем к новым координатам U и V так, чтобы координатные линии были ортогональны, причем заметим, чтоv-линии – это прямолинейные образующие торса. При переходе к новым координатам потребуем, чтобы семейство v-линий осталось прежним, а u-линии изменились и стали перпендикулярны v-линиям. Таким образом, перед нами стоит задача отыскания ортогональных траекторий к прямолинейным образующим торса.
Рассмотрим первую квадратичную форму поверхности, которая при условии, что касательная плоскость к торсу является псевдоевклидовой.
Пусть S – гладкая поверхность, ![]() - ее векторное уравнение и
- ее векторное уравнение и ![]()
Первой квадратичной формой поверхности S называют выражение I=![]() .
.
Запишем это выражение подробнее. Имеем
![]()
откуда
![]() . (25)
. (25)
Выражение (25) в каждой точке поверхности S представляет собой квадратичную форму от дифференциалов du и dv.
Для коэффициентов первой квадратичной формы часто используют следующие обозначения:
![]() .
.
Таким образом первая квадратичная форма имеет вид:
![]() (26)
(26)
|
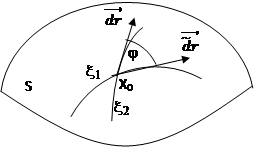
Угол между кривыми равен углу между касательными. Пусть гладкие кривые x1 и x2 лежат на поверхности S с векторным уравнением ![]() и пересекается в некоторой точке X0.
и пересекается в некоторой точке X0.
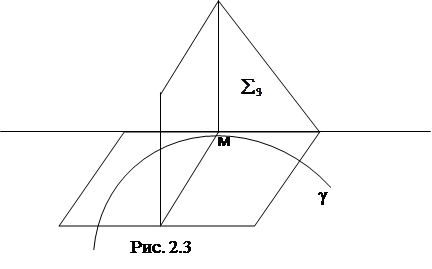
Вектор ![]() лежит в касательной плоскости к поверхности S в точке X0 (Рис.4.2).
лежит в касательной плоскости к поверхности S в точке X0 (Рис.4.2).
Значения дифференциалов ![]() можно выбрать так, чтобы
можно выбрать так, чтобы ![]() был вектором касательной к кривой x1 в точке X0. Достаточно взять (
был вектором касательной к кривой x1 в точке X0. Достаточно взять (![]() ) (здесь u=u(t) и v=v(t) – уравнения кривой x1 на поверхности S).
) (здесь u=u(t) и v=v(t) – уравнения кривой x1 на поверхности S).
Аналогично строится вектор ![]() - вектор касательной к кривой x2 в точке X0, отвечающий значениям дифференциалов
- вектор касательной к кривой x2 в точке X0, отвечающий значениям дифференциалов ![]() ,
, ![]() функций, определяющих кривую x2:
функций, определяющих кривую x2:
![]() .
.
Поэтому
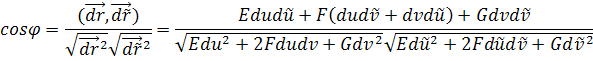
Требуется, чтобы ортогональные линии были ортогональны, т.е.
![]()
Учитывая, что u – естественный параметр, найдем коэффициенты E, F, G:
![]()
![]()
![]()
Подставляя полученные выражения в (26) имеем
![]()
Воспользовавшись (27) и полученными выражениями для коэффициентов, получим ![]() Разделим последнее равенство на
Разделим последнее равенство на ![]() , получим
, получим
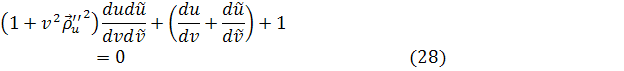
Исходное семейство линий задано дифференциальным уравнением
![]() , а ортогональные траектории получены в виде
, а ортогональные траектории получены в виде ![]() Подставляя эти выражения в (28), имеем уравнение для
Подставляя эти выражения в (28), имеем уравнение для ![]() , из которого
, из которого ![]() . Учитывая, что исходное семейство линий – это v-линии, для которых du=0, а значит l=0, получим m=-1. Таким образом,
. Учитывая, что исходное семейство линий – это v-линии, для которых du=0, а значит l=0, получим m=-1. Таким образом, ![]() , решая это дифференциальное уравнение, находим u+v=const – условие ортогональности траекторий. Итак, искомая замена координат имеет вид:
, решая это дифференциальное уравнение, находим u+v=const – условие ортогональности траекторий. Итак, искомая замена координат имеет вид:
![]()
Тогда обратная замена:
![]()
Уравнение торса в новых координатах примет вид:
![]()
Обозначим U, V теми же символами u, v тогда уравнение торса перепишется следующим образом:
![]() .(29)
.(29)
Рассмотрим на торсе (29) кривую
u=u(t), v=v(t).(30)
Получим ее уравнение в виде:
![]() . (31)
. (31)
Направляющий вектор касательной:
![]() . (32)
. (32)
Касательная к любой кривой, лежащей на торсе и проходящей через данную точку N, лежит в плоскости ![]() Эта плоскость будет называться касательной плоскостью к торсу и обозначается
Эта плоскость будет называться касательной плоскостью к торсу и обозначается ![]()
Найдем векторы ![]() . Из уравнения (29) получим:
. Из уравнения (29) получим:
![]() .
.
Таким образом, плоскость ![]() определяется точкой L торса и векторами
определяется точкой L торса и векторами ![]() , и следовательно, совпадает с соприкасающейся плоскостью ребра возврата g.
, и следовательно, совпадает с соприкасающейся плоскостью ребра возврата g.
|
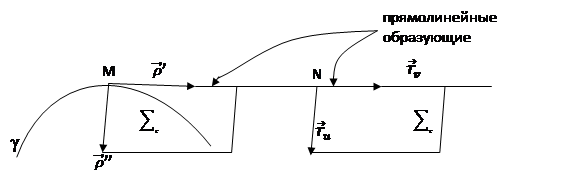
Получена теорема.
Теорема 4.1. Касательная плоскость к торсу в произвольной точке прямолинейной образующей совпадает с соприкасающейся плоскостью к ребру возврата в точке касания прямолинейной образующей.
Построим канонический репер в произвольной точке N торса. Будем считать параметр u естественным параметром ребра возврата. Тогда согласно
(9): ![]()
Введем следующие обозначения: ![]()
Тогда ![]() - вектор мнимой длины, а
- вектор мнимой длины, а ![]() - вектор единичной длины, взаимно ортогональные и лежат в касательной плоскости к торсу в точке N, совпадающей с соприкасающейся плоскостью ребра возврата, причем
- вектор единичной длины, взаимно ортогональные и лежат в касательной плоскости к торсу в точке N, совпадающей с соприкасающейся плоскостью ребра возврата, причем ![]() идет по прямолинейной образующей, а
идет по прямолинейной образующей, а ![]() ему ортогонален.
ему ортогонален.
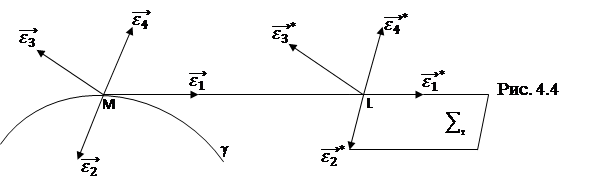
Вектора ![]() получим из векторов
получим из векторов ![]() соприкасающегося репера ребра возврата параллельным переносом в точку L. При этом получим репер
соприкасающегося репера ребра возврата параллельным переносом в точку L. При этом получим репер ![]() в произвольной точке L торса, с условием
в произвольной точке L торса, с условием
![]() .(33)
.(33)
Уравнение (33) целиком определяется торсом. Этот репер ![]() будем называть каноническим репером торса.
будем называть каноническим репером торса.
Найдем деривационные формулы канонического репера торса![]() с учетом того, что
с учетом того, что ![]() зависят только от u. С учетом (14) и (15):
зависят только от u. С учетом (14) и (15):
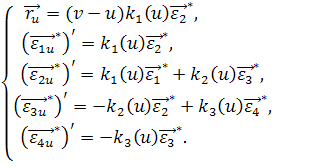 и
и 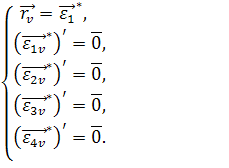 (34)
(34)
§5. Линии на торсах пространства Минковского
Рассмотрим торс в пространстве Минковского, заданный уравнением (29) ![]() .
.
Будем считать, что соприкасающийся флаг ребра возврата ![]() имеет тип 50: {M, 1R1, 1R2, 1R3, 1R4}, где параметр u есть естественный параметр на ребре возврата
имеет тип 50: {M, 1R1, 1R2, 1R3, 1R4}, где параметр u есть естественный параметр на ребре возврата ![]() . В данном случае на торсе строится канонический репер {M,
. В данном случае на торсе строится канонический репер {M, ![]() }. Деривационные формулы этого репера имеют вид (34).
}. Деривационные формулы этого репера имеют вид (34).
Определение 5.1. Кривая d: u=u(t); v=v(t) (35) на торсе Т называется (k,n) – геодезической, если соприкасающаяся n - плоскость этой кривой в каждой точке содержит k – мерную нормаль к торсу.
Возможны варианты: (1,2); (1,3); (2,3). Выясним существуют ли такие геодезические кривые на торсе данного типа. Касательная плоскость к торсу в точке L есть плоскость ![]() , а нормальная плоскость к торсу
, а нормальная плоскость к торсу ![]() . Найдем соприкасающуюся 2-плоскость линии d: r=r(u(t),v(t)). Эта плоскость определяется так:
. Найдем соприкасающуюся 2-плоскость линии d: r=r(u(t),v(t)). Эта плоскость определяется так: ![]() . Находим производные вектор - функции, преобразуем их с помощью деривационных формул (34):
. Находим производные вектор - функции, преобразуем их с помощью деривационных формул (34):
![]() (36)
(36)
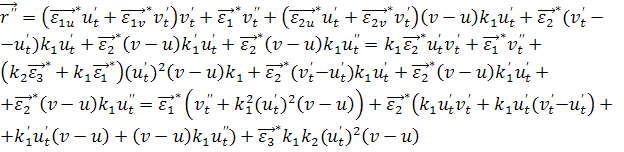 (37)
(37)
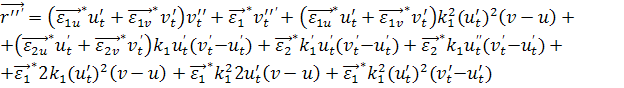 +
+![]() +
+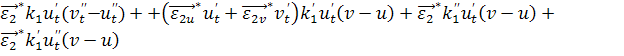 +
+
![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+
+![]() +
+
+![]() +
+
+![]() +
+
+![]() +
+![]() +
+
+![]() +
+
+![]() +
+
+![]() +
+![]() +
+![]() +
+
+![]()
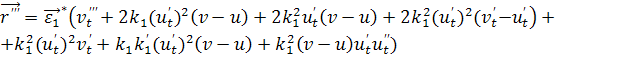 +
+
+![]() (
(![]()
+![]() +
+![]()
+![]() )+
)+![]() (
(![]() +
+![]() )+
)+![]() (38)
(38)
Нормаль к торсу ![]() зададим в виде:
зададим в виде: ![]() . С другой стороны, нормаль к поверхности, исходя из определения, содержится в соприкасающейся 2-плоскости
. С другой стороны, нормаль к поверхности, исходя из определения, содержится в соприкасающейся 2-плоскости ![]() , т.е.
, т.е. ![]() . Составим уравнение
. Составим уравнение
![]() =p(
=p(![]() )+q(
)+q(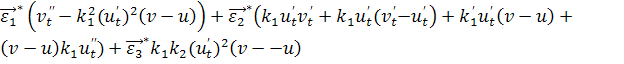 ).
).
Сгруппировав коэффициенты при ![]() , получаем систему:
, получаем систему:
|
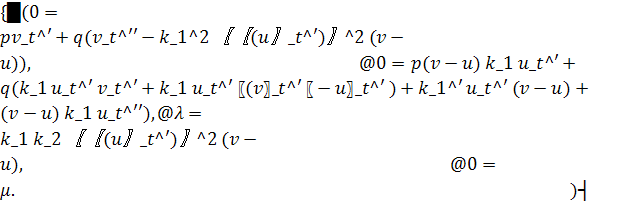
Из системы видим, что если (1,2) – геодезическая линия существует, то она определяется нормалью ![]() . Учитывая этот факт, преобразуем систему следующим образом:
. Учитывая этот факт, преобразуем систему следующим образом:
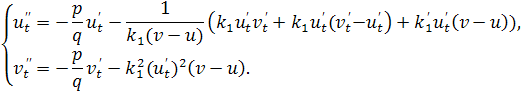
Таким образом, уравнение (1,2) – геодезической линии можно представить в виде нормальной системы дифференциальных уравнений:
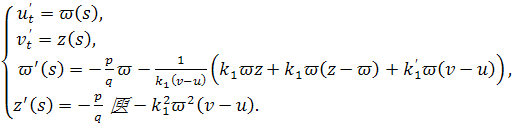 (39)
(39)
Теорема Пикара. Если правые части системы
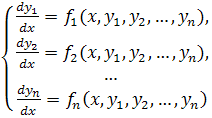
в некоторой окрестности начальной точки (![]() ) имеют непрерывные в этой окрестности частные производные по
) имеют непрерывные в этой окрестности частные производные по ![]() , то система имеет единственное решение, определенное в некоторой окрестности точки
, то система имеет единственное решение, определенное в некоторой окрестности точки ![]() и удовлетворяющее начальным условиям
и удовлетворяющее начальным условиям
![]() .
.
Согласно теореме Пикара система (39) имеет единственное решение. Значит, через каждую точку торса в каждом направлении касательной плоскости проходит единственная (1,2) – геодезическая линия.
Пусть d: r=r(u(t),v(t)) на торсе является (2,2) – геодезической. Тогда, согласно определению, система (38’) должна быть разрешима при любых коэффициентах ![]() и
и ![]() , но т.к.
, но т.к. ![]() , то это условие не выполняется. Значит, на торсе с касательной псевдоевклидовой плоскостью не существует (2,2) – геодезических линий.
, то это условие не выполняется. Значит, на торсе с касательной псевдоевклидовой плоскостью не существует (2,2) – геодезических линий.
|
Теорема 5.1. Геодезических линий типа (2,2) на торсе нет.
Рассмотрим вопрос о существовании (1,3) – геодезических линий на торсе. Соприкасающуюся 3-плоскость к кривой в некоторой точке можем задать линейным уравнением
![]()
|
Таким образом, нормальная плоскость и соприкасающаяся 3-плоскость всегда имеют пересечение, являющееся не менее чем прямой. Значит, любая линия на рассматриваемой поверхности является (1,3)-геодезической.
§6. Асимптотические линии на торсе пространства Минковского
Определение 6.1. Направление на поверхности называется асимптотическим, если нормальная кривизна поверхности в этом направлении обращается в нуль.
Определение 6.2. Нормальной кривизной кривой на поверхности пространства Минковского называется проекция вектора кривизны этой кривой на нормальную плоскость к поверхности в этой точке.
Определение 6.3. Кривая на поверхности называется асимптотической линией, если в каждой своей точке она имеет асимптотическое направление.
Определение 6.4. Вектором кривизны кривой ![]() на поверхности пространства Минковского будем называть вектор
на поверхности пространства Минковского будем называть вектор ![]() , где s – естественная параметризация на этой кривой.
, где s – естественная параметризация на этой кривой.
Пусть ![]() - произвольная кривая на торсе. Построим канонический репер кривой в точке N:
- произвольная кривая на торсе. Построим канонический репер кривой в точке N: ![]() . Нормальная кривизна кривой
. Нормальная кривизна кривой ![]() в точке N – это проекция вектора кривизны
в точке N – это проекция вектора кривизны ![]() на нормаль к поверхности. В пространстве 1R4 к поверхности в данной точке существует целая плоскость нормалей, поэтому необходимо определить нормаль, на которую будет проецироваться вектор кривизны. Координаты вектора
на нормаль к поверхности. В пространстве 1R4 к поверхности в данной точке существует целая плоскость нормалей, поэтому необходимо определить нормаль, на которую будет проецироваться вектор кривизны. Координаты вектора ![]() в репере
в репере ![]() согласно формуле (37) равны:
согласно формуле (37) равны:
![]()
![]() º(A;B;C;0)
º(A;B;C;0)
Нормальную кривизну ![]() определим как длину отрезка NL1, где L1 – точка пересечения плоскости
определим как длину отрезка NL1, где L1 – точка пересечения плоскости ![]() и проходящей через точку L, с нормальной плоскостью
и проходящей через точку L, с нормальной плоскостью ![]() . Определим координаты точки L1:
. Определим координаты точки L1:![]() x1=0, x2=0,
x1=0, x2=0, ![]() x3=0, x4=0; Þ
x3=0, x4=0; Þ![]() x3=C, x4=0. Значит,
x3=C, x4=0. Значит, ![]() , т.е. нормальная кривизна кривой
, т.е. нормальная кривизна кривой ![]() на торсе пространства Минковского, с псевдоевклидовой касательной плоскостью, является действительной величиной.
на торсе пространства Минковского, с псевдоевклидовой касательной плоскостью, является действительной величиной.
Определим геодезическую кривизну ![]() кривой
кривой ![]() как длину отрезка NL2, где L2 – точка пересечения плоскости
как длину отрезка NL2, где L2 – точка пересечения плоскости ![]() с касательной плоскостью
с касательной плоскостью ![]() . Определим координаты точки L2:
. Определим координаты точки L2: ![]() x3=0, x4=0;
x3=0, x4=0;![]() x1=0, x2=0; Þ
x1=0, x2=0; Þ![]() x1=A, x2=B. Следовательно, координаты точки L2:
x1=A, x2=B. Следовательно, координаты точки L2:
![]() x1=A, x2=B, x3=0, x4=0. |NL2|=
x1=A, x2=B, x3=0, x4=0. |NL2|=![]() .
.
Рассмотрим нормальную кривизну ![]() . Справедлива формула первой квадратичной формы поверхности:
. Справедлива формула первой квадратичной формы поверхности: ![]() , таким образом,
, таким образом,
![]() (40)
(40)
На торсе с касательной псевдоевклидовой плоскостью асимптотические линии есть прямолинейные образующие торса, а также линии v=u.
Нормальная кривизна кривой ![]() в точке N зависит только от
в точке N зависит только от ![]() , т.е. от направления в касательной плоскости.
, т.е. от направления в касательной плоскости.
Заключение
В работе исследуется геометрия поверхностей пространства Минковского.
В пространстве 1R4 рассматриваются торсы, то есть поверхности образованные касательными к некоторой кривой пространства Минковского, называемой ребром возврата для этого торса. Рассмотрен класс таких поверхностей, ребро возврата которых имеет соприкасающийся флаг вида {M, R1, 1R2, 1R3}.
Для торсов такого класса решены следующие задачи:
1. построен канонический репер торса;
2. получены деривационные формулы построенного канонического репера;
3. определено понятие (n,k) – геодезических линий на торсе;
4. получена теорема о существовании (1,2)-, (2,3) – геодезических линий на исследуемом торсе;
5. вводится обобщение понятия асимптотических линий на поверхности пространства Минковского, находятся асимптотические линии на торсе рассматриваемого класса.
Результаты проводимого исследования докладывались на республиканской научно-практической конференции молодых ученых, аспирантов и студентов «Современные проблемы математического моделирования и новые образовательные технологии в математике» (Брест, 23 апреля 2009 года). На основании доклада будет напечатана статья в сборнике материалов конференции.
Список использованных источников
1. Атанасян, Л.С. Геометрия: учеб. пособие в 2 ч./ Л.С. Атанасян, Г.Б. Гуревич. – М.: Просвещение, 1976. – Ч.2. – 488 с.
2. Базылев, В.Т. Геометрия: в 2 т./ В.Т. Базылев, К.И. Дуничев. - М.: Просвещение, 1972. – Т.2. – 352 с.
3. Бакельман, И.Я. Введение в дифференциальную геометрию: учебное пособие/ И.Я. Бакельман, А.Л. Вернер, Б.Е. Кантор. – М.: Наука, 1973. – 437 с.
4. Матвеев, Н.М. Дифференциальные уравнения: учеб. пособие для студ. пед. ин-тов по физ. – мат. спец./ Н.М. Матвеев. – М.: Просвещение, 1988. – 464 с.
5. Погорелов, А.В. Геометрия: учебник для студентов математических специальностей университетов и пед. институтов/ А.В. Погорелов. – М.: Наука, 1974. – 173 с.
6. Позняк, Э.Г. Геометрия: учеб. пособие/ Э.Г. Позняк, Е.В. Шикин. - М.: изд-во МГУ, 1990. – 384 с.
7. Рашевский, П.К. Курс дифференциальной геометрии/ П.К. Рашевский. – М.: Просвещение, 1982. – 220 с.
8. Рашевский, П.К. Риманова геометрия и тензорный анализ/ П.К. Рашевский. – М.: Наука, 1964. – 538 с.
9. Тайманов, И.А. Лекции по дифференциальной геометрии/ И.А.Тайманов. – Ижевск: Институт компьютерных исследований, 2002. – 176 с.
10. Фиников, С.П. Дифференциальная геометрия: курс лекций для мат. ф-та МГУ/ М.С. Фиников. – М.: московский университет, 1961. – 150 с.
11. Шварц, Д. Дифференциальная геометрия и топология/ Д. Шварц. – М.: Мир, 1970. – 224 с.
0 комментариев