Министерство образования российской Федерации
ЧЕЛЯБИНСКИЙ ЮРИДИЧЕСКИЙ КОЛЛЕДЖ
Домашняя контрольная работа
по дисциплине "Математика"
для студентов заочной формы обучения специальностей 0601 "Экономика и бухгалтерский учет",
0602 "Менеджмент"
Челябинск
2008
Задание № 1
Вычислить пределы:
а)
. б) 
; 
.
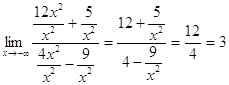в)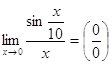 
;
Первый замечательный предел
.
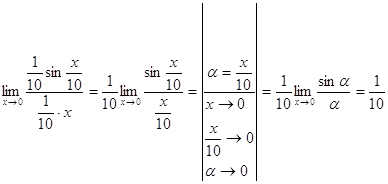г) 
= [1]
Второй замечательный предел
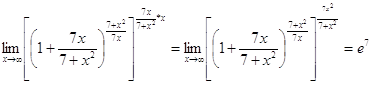
Задание № 2
Продифференцировать функцию:
а) 
б) 
Задание № 3
Исследовать функцию и построить ее график:
1) Д (у) =
2) y = 0 при 
; 2х-3=0; 2х=3; х=1,5
при х = 1,5 решения нет
3) 
=0;
2x-19=0 или 
x=9.5 
=0
Д=144-144=0
Критические точки 9,5; 1,5
| Х | ( | 1.5 | (1,5;9.5) | 9.5 | (9.5; |
| Y’ | - | - | - | ||
| Y |
| Не существует |
| 0,5 |
|
;1.5)
)
4)y’’ =
x< 1.5
, f¢¢> 0, график функции вогнут вверх
х> 1.5 , f¢¢< 0 , график функции вогнут вниз
5) Асимптоты графика функции
, то прямая х = 1,5 является вертикальной асимптотой
Кривая не имеет наклонных асимптот
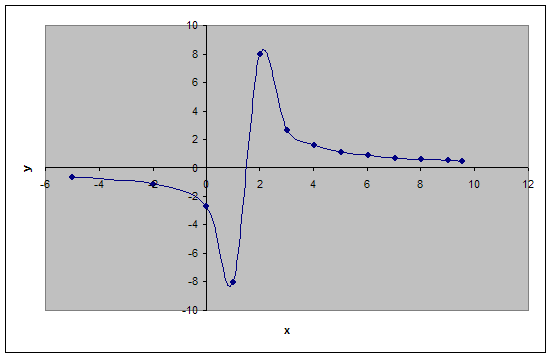
Задание № 4
Вычислить неопределенный интеграл:
a)
=
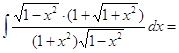
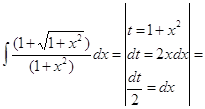
б) 
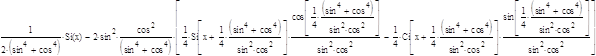+C
в)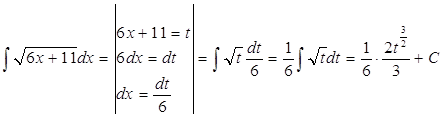 
=
Задание № 5
Вычислить определенный интеграл:
а)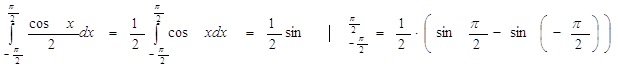
=
=
б)
в)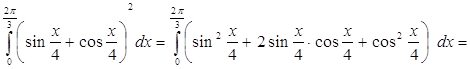 
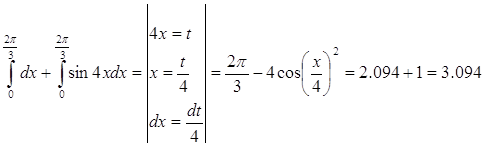
Задание № 6
Вычислить площадь криволинейной трапеции, ограниченной графиками функций: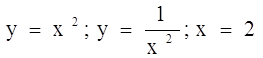 
Найдем координаты т. пересечения функций:
; 
;
или 
, 
т.е. (х-1)(х-1)(х+1)(х+1) и (х-2)
Пересечение линий зададут пределы интегрирования:
Площадь фигуры ограниченной линиями :
(ед)
Задание №7
Даны две матрицы А и В. Найти:
а) АВ; б) ВА; в) А-1; г) АА-1
8 вариант
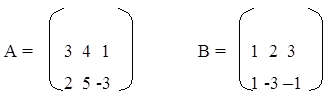
Данная матрица не вырожденная решения нет. ( т.к.) это скорее всего ошибка документа то решим задание варианта 7.
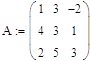
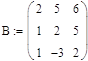
Решение:
а)
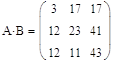
б)
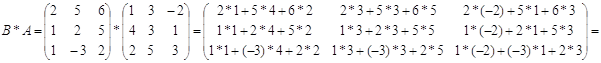
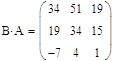
в)
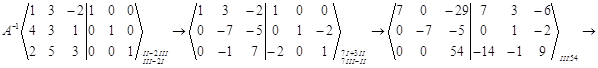
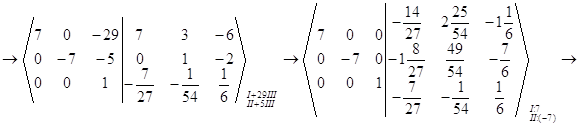
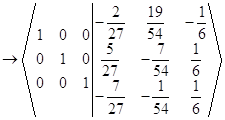
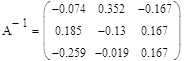
г)
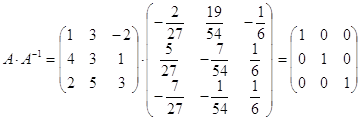единичная матрица
|
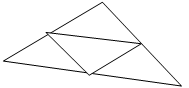
А (0; -3; 2)
В (1; 2; 3)
|
Решение
|
|
; 
; 
.
; 
; 
.
; 
; 
.
Ответ: координаты середин сторон треугольника М(0,5; -0,5; 2,5); N(2;-0,5;-0,5); D(2,5;2;0).
Похожие работы
... условий: y(x0)=y0, . Эти начальные условия дают соответственно n уравнений , , , ……………………………… , решая которые относительно c1, c2 , …, cn находят значения этих постоянных. Например, для дифференциального уравнения 1-го порядка общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0). Геометрическая ...
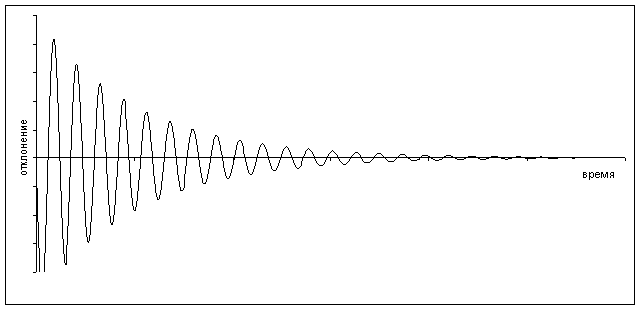
... bo=31,20 Запишем это уравнение в стандартной форме. Для этого разделим (1) на ao: - +y(t)=g(t) -T1 +y(t)=kg(t) (2), где k=-коэффициент передачи, T1=,T22=-постоянные времени. Если корни характеристического уравнения для дифференциального уравнения 2-го порядка комплексные (это выполняется при T1<2T2), то оно является колебательным. Проверим это для нашего уравнения: T1=0,042 2T2=0,14 ...
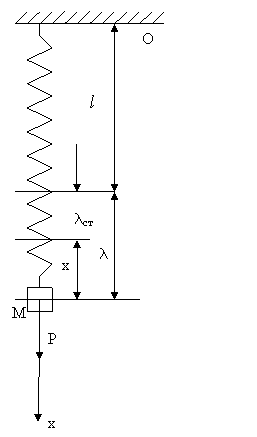
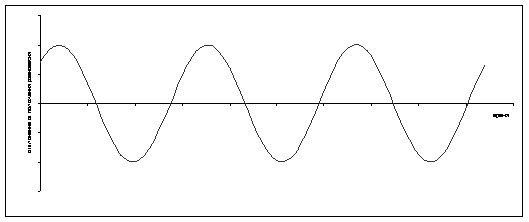
... уравнение в виде: или, обозначив с/m через k2, (1) Полученное уравнение определяет так называемые свободные колебания груза. Оно называется уравнением гармонического осциллятора. Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Его характеристическое уравнение: имеет мнимые корни , соответственно этому общее решение Для выяснения ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
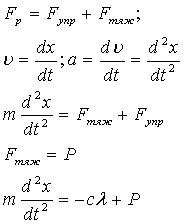
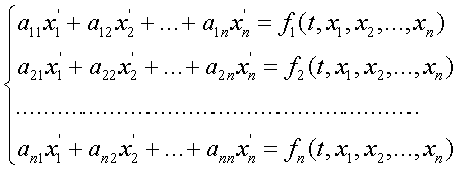
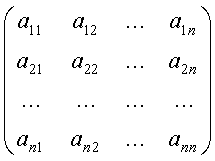
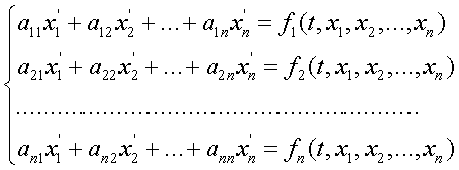
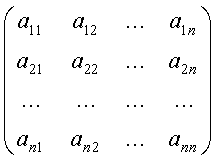
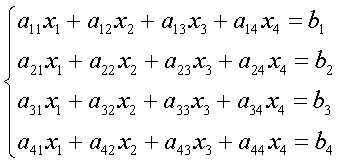
0 комментариев