Определение динамических свойств объектов с помощью дифференциальных уравнений может быть пока успешно выполнена только для сравнительно простых объектов. Как правило, в редких случаях можно при небольшой затрате времени составить достаточно точное дифференциальное уравнение объекта.
В настоящие время при составлении дифференциальных уравнений элементов и систем регулирования принято пользоваться безразмерными переменными величинами. Для этого отклонения величин относят к каким-либо постоянным (базовым) значениям величин, например к максимальным или средним (номинальным). Выражая входную и выходную величины элемента (или системы) в долях от этих базовых величин, вводят безразмерные координаты.
Например, уравнение
(С*d (DQ) /СC*dt) + DQ= 2*I0*R*DI/ СC*F (1)
DI/I = XВХ характеризует относительное отклонение входной величины от базового значения, а DQ/ Q0 = Хвых относительное отклонение выходной величины. Для перехода от размерной формы записи дифференциального уравнения к безразмерной производят замену абсолютных координат относительными. Так, например, уравнение (1) можно записать в безразмерной форме, заменив:
DQ = Q0 *Хвых и DI = I *XВХ
Тогда
С* Q0* d Хвых / СC* F* dt + Q0 Хвых = 2* I02* R* XВХ/ СC*F
Разделив обе части уравнения на Q0, получим:
С* d Хвых / СC* F* dt + Хвых = 2* I02* R* XВХ/ СC*F* Q0
Обозначим:
С/ СC* F= Т 2* I02* R/ СC*F* Q0 = R
Коэффициенты при производных от выходной величины называются постоянными времени и имеют размерность времени
В самом деле,
С[дж/град]/ СC[вт/см2*град]* F[ см ]= С/ СC* F[дж*см2*град/град*вт*см2]
Коэффициент К при XВХ называется коэффициентом усиления, и естественно должен быть безразмерным:
2* I02[А2]* R[Ом]/ СC[ вт/см2*град ]*F[ см ]* Q0[град] =
= 2* I02* R/ СC*F* Q0[А2*Ом*см2*град/Вт*см2*град] =
= 2* I02* R/ СC*F* Q0[0] = К
Уравнение (1) с учетом введённых обозначений будет иметь в безразмерной форме следующий вид:
Т* Х/ вых + Х вых = К* Х вх (2)
Определим для примера уравнение кривой разгона термической печи, дифференциальное уравнение которой было введено ранее:
Т* Х/ вых + Х вых = К* Х вх
Будем искать решение этого уравнения в виде
Х вых = С*еrt + K* Х вх 0
Где r и С подлежат определению
Подставляя значения Х вых и Х/ вых в уравнение (2). Получим
Т* С*r*еrt + С*еrt = 0
Сокращая на С*еrt будем иметь:
Т* r + 1 = 0
Откуда r = - 1/Т и решение примет вид
Х вых = К* Х вх 0 (1-е-t/T)
При t = 0 Х вых = 0 следовательно С = К* Х вх 0. тогда уравнение кривой разгона будет:
Х вых = К* Х вх 0 (1-е-t/T)
График кривой разгона:
При t = ¥ выходная величина Х вых достигает предельного значения
Х вых. уст = К* Х вх 0
Коэффициент усиления К определяет отношение установившихся значений выходной величины к входной:
К = Х вых. уст/ Х вх 0
Коэффициент усиления может быть непосредственно найден из графика переходной функции; постоянная времени Т характеризует инерционность процесса.
Таким образом, кривые разгона дают наглядное представление о характере протекания переходных процессов в системе или объекте.
Похожие работы
... связывают в зависимость. 3. Через параметры элемента записывают уравнения этого элемента. 4. Из системы уравнений отдельных элементов получают дифференциальное уравнение АСР в целом. Для решения дифференциальных уравнений в теории автоматического регулирования пользуются так называемым операторным методом или методом преобразования Лапласа. Основное достоинство данного метода состоит в том, ...
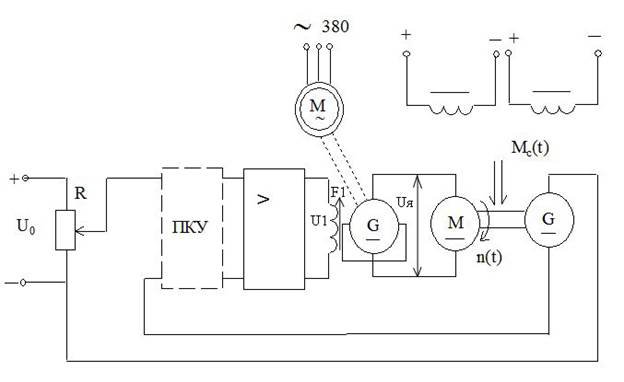
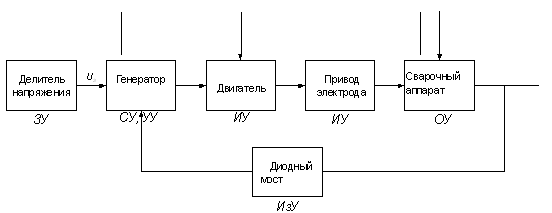
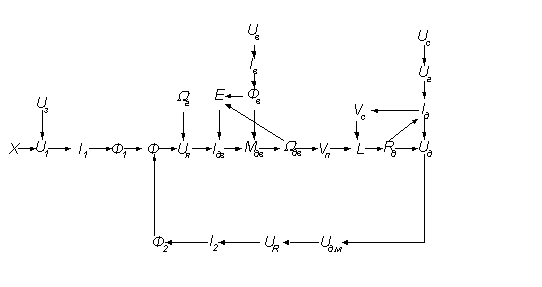
... свидетельствует о том, что это статическая система. 2.3 РАЗРАБОТКА ФУНКЦИОНАЛЬНОЙ СХЕМЫ САР U0 Рисунок 2.1 – Функциональная схема системы автоматического регулирования частоты вращения двигателя постоянного тока с электромашинным усилителем мощности 2.4 АНАЛИЗ ДЕЙСТВУЮЩИХ НА СИСТЕМУ ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ, АНАЛИЗ ИХ ВЛИЯНИЯ НА СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ САР К основному, оказывающему самое ...
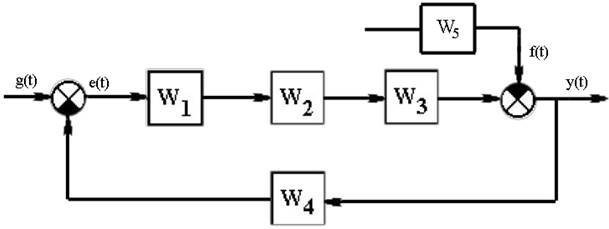
... работы Целью работы является анализ частотных характеристик разомкнутых и замкнутых систем, получение навыков по использованию критерия устойчивости Найквиста. В работе предусматривается исследование трех систем, различающихся видом передаточной функции (ПФ) разомкнутого контура. Варианты значений параметров ПФ приведены в табл. 3.1. Замкнутая система построена по типу классической следящей ...
... Y(t), ..., Z(t) в тот же момент: (3) Такой вид математической модели означает, что моделируемый объект рассматривается как статический (безинерционный). САР напряжение сварочной дуги-это статическая система, так как всегда будет присутствовать ошибка регулируемого параметра, в силу нелинейной зависимости числа оборотов двигателя от величины магнитного потока возбуждающей ...


0 комментариев