Метод наименьших квадратов

1.4 Метод наименьших квадратов

Для нахождения аналитического уравнения, по которому производится выравнивание уровней временного ряда, применяют различные способы. Один из таких способов – метод наименьших квадратов - основан на требовании о том, чтобы сумма квадратов отклонений фактических данных от выровненных была наименьшей:

(у₁ – у₁)² + (у₂ – у₂)² + . . . + (у_n – y_n)² = S.

S должно быть наименьшим (минимальным)

Принцип, положенный в основу метода наименьших квадратов, может быть записан в сжатом математическом виде следующим образом:

∑ (y – y_t)² = min. (1.4.1)

Из курса математического анализа известно, что при нахождении минимума функции нужно найти частные производные и приравнять их к нулю. Найдём минимум функции, используя уравнение параболы.

Имеем:

∑ (y – y_t )² = S; (1.4.2)

заменяем:

y_t = a₀ + a₁ t + a₂ t ²

и получаем:

∑( y - a₀ - a₁ t - a₂ t ² )² = S.

Находим частные производные функции S сначала по параметру а₀, а затем по а₁ и а₂, и приравниваем их к нулю.

;

; (1.4.3)

.

Преобразовывая, получаем:

 ;

 ; (1.4.4)

 .

 

Полученная система называется системой нормальных уравнений для нахождения параметров а₀ , а₁ и а₂ при выравнивании по параболе второго порядка.

При выравнивании по показательной функции y_t = a₀ a₁^tпараметры а₀ и а₁ определяются по методу наименьших квадратов отклонений логарифмов путём решения системы нормальных уравнений:

 ; (1.4.5)

 .

1.5 Приведение уравнения тренда к линейному виду

Если тренд представляет собой нелинейную функцию, то методы линейного регрессионного анализа для оценки его параметров неприменимы. Но к некоторым нелинейным функциям мы можем применить такие преобразования, которые приведут нас к линейному уравнению.

Если наш тренд представлен степенной линией регрессии, то есть он имеет вид:

y_t = a₀t^a1, (1.5.1)

то логарифмируя обе части равенства, получим:

ln y_t = ln a₀ + a₁ ln t.

Отсюда видно, что, введя новые переменные

z = ln y_t , x = ln t,

мы получим уравнение вида

z = b₀ +a₁x,

где b₀ = ln a₀. Это обычное линейное уравнение.

Если линия тренда – парабола второго порядка

y_t = a₀ + a₁ t + a₂ t ² ,

то заменой вида:

х₁ = t, x₂ = t ²,

мы получим линейную функцию двух переменных:

y_t = a₀ + a₁ х₁ + a₂ х₂ .

Оценку параметров такой функции можно провести методами линейного регрессионного анализа для множественной регрессии. [5, c.29]

Далее приведём основные понятия регрессионного анализа, которые используются для оценки параметров.

 

1.6 Оценка параметров уравнения регрессии

Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции r_yt. Существуют разные модификации формулы линейного коэффициента корреляции. Некоторые из них приведены ниже:

 , (1.6.1)

или

. (1.6.2)

Как известно, линейный коэффициент корреляции находится в пределах:

 -1 ≤ r_yt ≤ 1.

Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в её линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю ещё не означает отсутствия связи между признаками.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции r_yt², называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у_t, объясняемую регрессией, в общей дисперсии результативного признака:

 (1.6.3)

где

 

общая дисперсия результативного признака у;

остаточная дисперсия, определяемая, исходя из уравнения регрессии

у_t = f(t).

Соответственно величина 1 – r² характеризует долю дисперсии у, вызванную влиянием остальных, не учтённых в модели факторов.

Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции R:

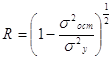 (1.6.4)

Иначе, индекс корреляции можно выразить как

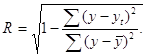
Величина данного показателя находится в границах: