Навигация
1 Годограф Найквиста.
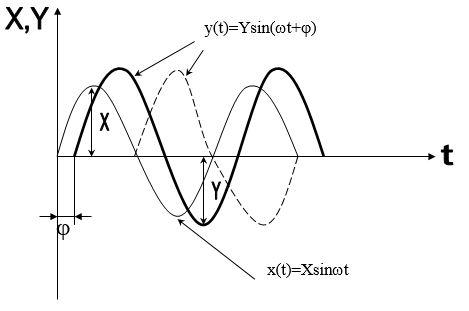
Представление частотной характеристики
на плоскости комплексной переменной в зависимости от частоты называется амплитудно-фазовой частотной характеристикой (а.ф.ч.х.). Вообще говоря, с изменением частоты w от нуля до бесконечности (0 < w <¥) вектор 
в плоскости комплексного переменного будет поворачиваться и его конец опишет некоторую кривую, называемую годографом. Применительно с частотным характеристикам этот годограф называется годографом Найквиста (а.ф.ч.х.).
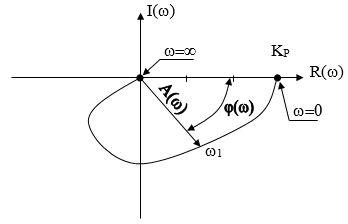
На рисунке 1 приведен типичный пример годографа Найквиста в положительном диапазоне частот (0 < w <¥). На нем показаны все составляющие частотной характеристики как комплексной функции вещественного аргумента.
Иногда, (например, в ППП Control System Toolbox) годограф строится во всем диапазоне частот (-¥ < w <¥). Не трудно доказать, что при отрицательных значениях частот годограф симметричен годографу при положительных значениях частот (относительно вещественной оси).
Рисунок 1 - Годограф Найквиста
2 Диаграммы Боде
Логарифмические амплитудные и фазовые частотные характеристики (ЛЧХ), называемые диаграммами Боде, получили гораздо большее распространение, чем годографы Найквиста.
Прологарифмировав выражение частотной характеристики (через амплитудную и фазовую), получим, что ее логарифм равен сумме логарифма амплитудной характеристики и фазовой характеристики:
.
Две характеристики 
и 
, построенные в логарифмическом масштабе частот (
), называются натуральными логарифмическими амплитудными и фазовыми частотными характеристиками.
В теории автоматического управления используются десятичные логарифмы. За единицу измерения принимается децибел (
) и рассматривают две характеристики: 
и , построенные в логарифмическом масштабе частот. Именно они называются логарифмическими амплитудными и логарифмическими фазовыми характеристиками соответственно.
Логарифмический масштаб частот связан с некоторыми особенностями в терминологии. При двукратном изменении частот говорят, что частота изменилась на октаву, а при десятикратном – на декаду. Иначе говоря, октава – отрезок логарифмической оси частот, между произвольным значением частоты и ее удвоенным значением.
Декада – отрезок логарифмической оси частот между произвольным значением частоты и в десять раз большим значением:
.
При графическом изображении логарифмических характеристик придерживаются некоторых правил. Точка, соответствующая нулевому значению частоты лежит слева в бесконечности, т.к. lg0 = -¥. Поэтому ось ординат проводится через любую точку оси частот так, чтобы справа располагалась та часть ЛЧХ, которую нужно исследовать, а слева – для описания которой достаточно качественных характеристик. Слева обычно остается та часть фазовой характеристики, которая мало отличается от нуля (или другого постоянного значения). То же самое можно сказать и о коэффициенте наклона амплитудной характеристики. Слева обычно оставляют ту часть амплитудной характеристики, коэффициент наклона которой мало отличается от нулевого значения (или другого постоянного значения.
Амплитудную и фазовую характеристики изображают на одном рисунке с общей осью частот. Ось частот разбивается на декады и, может быть, октавы, причем каждая декада разбивается на октавы отдельно. Для удобства под точками этой оси принято записывать не значения логарифмов частот, а значения самих частот. Обе характеристики имеют общую ось ординат, но две разные разметки: в децибелах для амплитудной характеристики и в радианах (или градусах) для фазовой.
Удобство логарифмических характеристик заключается в возможности простого определения амплитудных характеристик последовательного соединения звеньев и спрямления амплитудных характеристик, как будет показано ниже.
Передаточная функция последовательного соединения звеньев равна произведению передаточных функций соединяемых звеньев. Поэтому
.
Вместе с тем
.
Определим отсюда выражение логарифмических характеристик последовательного соединения звеньев:
,
Таким образом, логарифмические характеристики последовательного соединения складываются. Это относится как к амплитудным, так и к фазовым характеристикам.
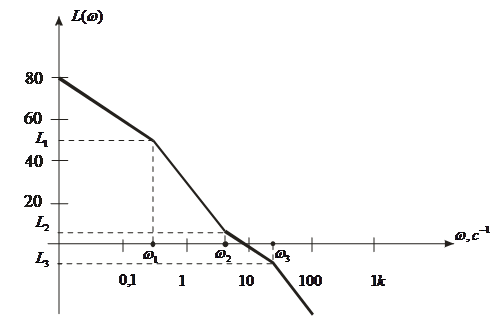
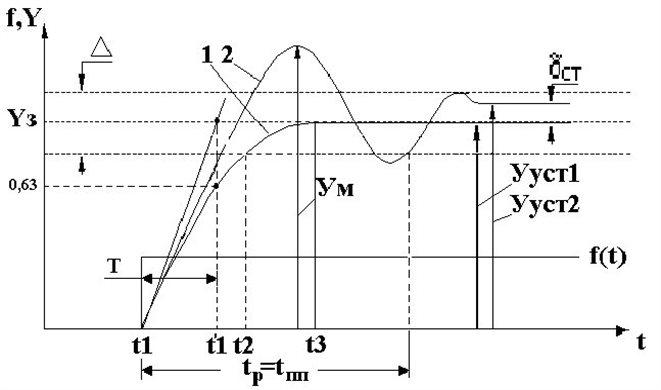
На рисунке 2 в качестве примера изображены логарифмические характеристики (диаграммы Боде) системы с передаточной функцией
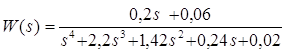
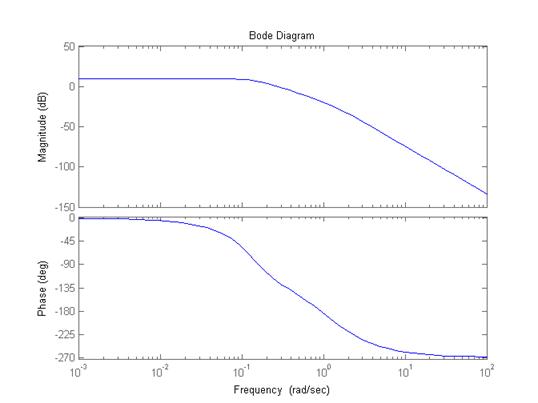
Рисунок 2 - Логарифмические частотные характеристики (ЛЧХ)
ЛИТЕРАТУРА
1. Мирошник И.В. Теория автоматического управления. Линейные системы. - СПб.: Питер, 2005.
2. Филлипс Ч., Харбор Р. Системы управления с обратной связью. М.: Лаборатория Базовых Знаний, 2001.
3. Методы классической и современной теории автоматического управления в 3-х т. Т.1: Анализ и статистическая динамика систем автоматического управления / Под ред. Н.Д. Егупова. – Изд. МГТУ им. Н.Э. Баумана, 2000.
Похожие работы
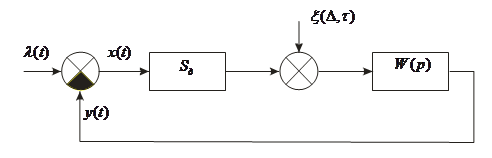
... в точке подачи обратной связи и определяется как передаточная функция от ошибки x(t) к управляемой величине y(t) . Передаточные функции в обобщенной структурной схеме радиотехнической следящей системы Основная передаточная функция – передаточная функция замкнутой системы. Определяется отношением изображений по Лапласу управляемой величины и задающего воздействия: где Передаточная ...
12795
0
3
... видно, что фаза выходного сигнала не более 140°. Это означает, что система не достигает критической фазы 180° и работает в устойчивом режиме при любой частоте воздействий на систему. Рисунок 11 – АФЧХ Все приведенные характеристики представляют собой различные формы описания одних и тех же свойств элементов или систем. Имея одну характеристику, можно получить любую другую. По этим характеристикам ...
... , обозначаемой обычно К(р). Отношения любых переменных вектора неизвестных называются схемными функциями. Численный расчет или формирование аналитических выражений для схемных функций составляют основу задачи анализа линейных эквив. схем в частотной области. Согласно правилам Крамера, эти функции описываются линейной комбинацией отношений алгебраических дополнений матрицы А. Таким образом, в общем ...
... плана ФЭ. Большое разнообразие моделей РК приводит к необходимости использования разнообразных способов и технических средств для измерения их параметров. Как правило, статические и динамические параметры РК измеряют на разных технологических установках. Методы построения средств измерения для идентификации моделей РК могут быть сведены к следующим принципам, учитывающим особенности подключения ...
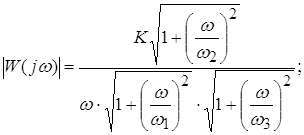
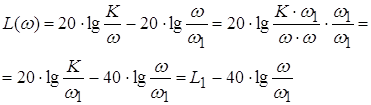
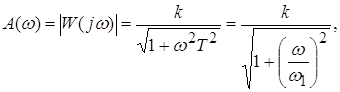
0 комментариев