Навигация
РАСЧЕТ МУФТЫ СЦЕПЛЕНИЯ
4. РАСЧЕТ МУФТЫ СЦЕПЛЕНИЯ
Большинство фрикционных муфт сцепления работают в условиях сухого трения, предполагающего отсутствие смазки между поверхностями. В последние годы начинают все шире применяться фрикционные устройства, работающие в масле в условиях граничного или полужидкостного трения.
В обоих случаях исходными данными при оценке свойств пары трения являются коэффициент трения и износостойкость. Трение и износ, как известно, неотделимые процессы, в большей мере зависящие как от материалов и состояния поверхностей, так и от условий работы фрикционных элементов в узле трактора.
Условия работы фрикционной муфты сцепления определяются не только видом трения, но и нагрузочными, скоростными и тепловыми режимами.
Коэффициент трения и износостойкость зависят от многих факторов, основными из которых являются удельное давление, скорость скольжения и температура поверхностей.
4.1 Расчет числа пар терния фрикционной муфты сцепления
Исходные данные:
максимальный момент двигателя - 386 Нм
Коэффициент запаса – β=2,0
Средний радиус поверхности трения RC=14 см
Ширина поверхности трения b=7 см
Пара трения сталь по металлокерамике. q=2.5 Мн/м2. µ=0,082. Полагаем что на поверхностях металлокерамических дисках имеются спиральные и радиальные каналы, занимающие 50% площади трения
![]() (4.1)
(4.1)
Принимаем Z=1. Значит Муфта сцепления однодисковая, работающая в масле.
4.2 Тепловой расчет
Определение температуры поверхностей дисков фрикционной муфты работающей в масле. Работа буксования L=120000дж, время буксования τ=2 с, начальная температур дисков t = 50ºC, толщина дисков 4 мм. Теплофизические коэффициенты металлокерамики берем λ=15,5 вт/м*град, (сγ)м=1,68*106 дж/м3*град, а=0,393*10-5 м2/сек, удельный расход масла ω=0,12*10-2м3/м2*сек, для спиральных и радиальных каналов на поверхностях ξ=0,78.
Полагаем, что диски с металлокерамическим покрытием имеют на поверхности трения спиральные и радиальные каналы. Толщина слоя металлокерамики равна 1,0 мм, а толщина стальной основы диска 3 мм. Теплофизические коэффициенты для таких дисков необходимо определять как для многослойной конструкции, т.е. необходимо найти их эквивалентные значения по известным из теории теплопроводности уравнениям:
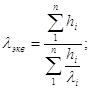
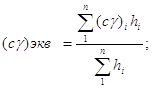 (4.2)
(4.2)
В нашем случае λэкв=27,2 вт/м*град (сγ)экв=3,97*106 дж/м3*град, аэкв=0,685*10-5 м2/сек
Температура поверхностей трения определяется по формуле:
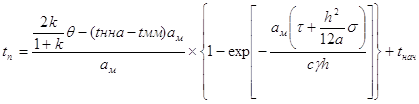 (4.3)
(4.3)
Находим расчетные коэффициенты:
Коэффициент распределения тепловых потоков
![]() (4.4)
(4.4)
Коэффициент теплоотдачи
ам=(сγ)мωξ=1580 дж/м2*град*сек
При том же тепловом потоке θ температура tn=221(1-е-0,174)+60=95 ºС.
Из теплового расчета видно, что при малой продолжительности буксования (однократное включение муфты) эффект охлаждения дисков маслом незначителен. Определяем время охлаждения дисков до начальной температуры после включения фрикционной муфты, работающей в масле, а также величину потерь мощности на разбрызгивание.
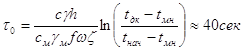 (4.5)
(4.5)
Величину потерь мощности на разбрызгивание находим по уравнению при условии, что зазор между дисками будет 0,5 мм, а относительная скорость вращения дисков 25 м/сек.
Nб=4,3*10-2-2,61*10-2*7*25/5*10-4=390 вт
4.3 Расчет тарельчатой пружины
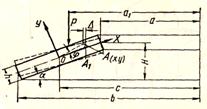
Рис. 4.1 Разрез тарельчатой пружины.
На рис.4.1 показан разрез тарельчатой пружины по основному рабочему участку (перья, идущие к центру на рисунке не показаны). При расчете этой пружины исходим из предположения, что под воздействием нагрузки Р прямоугольное сечение пружины не изменяет своей формы, а лишь поворачивается вокруг точки О.
Рассмотрим в сечении пружины точку А с координатами х и у. После поворота сечения эта точка переместится в положение А1 и приблизится к оси симметрии пружины на величину Δ:
Δ=[х cos (α-φ)- y sin (α-φ)] – (x cos α – y sin φ).(4.6)
Углы α и φ практически невелики, поэтому можно принять
![]()
![]()
![]()
![]()
Тогда
![]()
![]()
Относительное удлинение пружины равно:
![]()
![]() (4.7)
(4.7)
Нормальное напряжение:
![]()
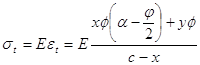 (4.8)
(4.8)
Номинальная сила в осевом сечении пружины будет
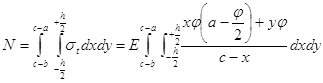 (4.9)
(4.9)
После интегрирования
![]()
Рассматривая условие равновесия полукольца (рис.4.2) убеждаемся, что N=0, тогда
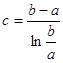
Максимальное напряжение будет при х=с-а и ![]()
Подставляя эти значения в уравнение (4.7), находим максимальное напряжение:
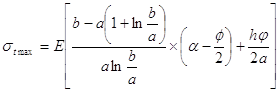
Учитывая, что
![]()
![]()
где ωn – деформация пружины в направлении действующей силы Р, находим:
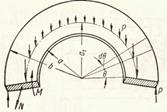
Рис.4.2 Условие равновесия полукольца.
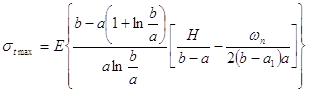 (4.10)
(4.10)
Находим изгибающий момент относительно оси х (относительно оси у пренебрегаем)
![]()
|
|
Рис.4.3 Примерная характеристика пружины
Используя все предыдущие выражения находим уравнение характеристики пружины:
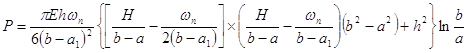
Примерная характеристика пружины приведена на рис. 4.3. При проектировании пружины следует выбирать ее предварительную осадку при включенной фрикционной муфте, на следующей части характеристика с таким расчетом, чтобы в процессе износа дисков трение пружины не уменьшалось.
Похожие работы
... навыки у докеров. 23. СИСТЕМА ОБЕСПЕЧЕНИЯ ПЕРЕГРУЗОЧНЫХ РАБОТ ТЕХНОЛОГИЧЕСКОЙ ОСНАСТКОЙ Система обеспечения оснасткой технологических процессов портовых перегрузочных работ включает: планирование поставки и производство механизмов и приспособлений; содержание их в исправном состоянии, т. е. регистрацию, освидетельствование с испытанием, периодические осмотры, техническое обслуживание и ...
... передаточных чисел Кинематическое передаточное число ix: Силовое передаточное число iy: iy=F1/N¢V=2754,82/2596,5=1,061. 6.3 Построение кривой жесткости подвески Для построения упругой характеристики подвески автомобиля ЗАЗ-1102 “Таврия” необходимо определить жесткость средней части подвески с1. Расчет жесткости подвески с1 проводится по выбранной частоте колебаний ω ...



0 комментариев