Навигация
Поведения системы в условиях малых колебаний
3. Поведения системы в условиях малых колебаний
3.1 Положения равновесия механической системы и их устойчивостьДля определения положения равновесия механической системы воспользуемся выражением для потенциальной энергии системы, которое было выведено нами во втором разделе курсовой работы (см. п. 4):
![]() (3.1.1)
(3.1.1)
Найдем возможные положения равновесия системы. Значение обобщенных координат в положениях равновесия есть корни системы уравнений:
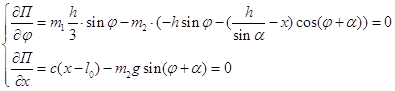
Решая систему уравнений, получаем два возможных положение равновесия:
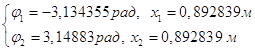 .
.
Для оценки устойчивости полученных положений равновесия определим обобщенные коэффициенты жесткости. Найдем все вторые производные потенциальной энергии (3.1) по обобщенным координатам:
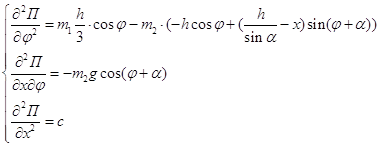
Для первого положения равновесия обобщенные коэффициенты жесткости равны:
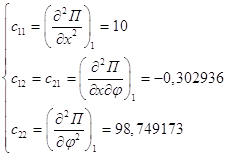
Воспользуемся критерием Сильвестра:
![]()
Для второго положения равновесия обобщенные коэффициенты жесткости равны:
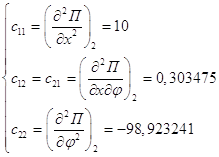
Воспользуемся критерием Сильвестра:
![]()
Таким образом, система принимает единственное устойчивое положение равновесия при: ![]()
3.2 Частоты главных колебаний. Уравнения движения материальной точки и твердого тела при колебаниях
Для нахождения частот и форм главных колебаний, выпишем полученные значения обобщенных коэффициентов инерции и жесткости в положении устойчивого равновесия, при: ![]() .
.
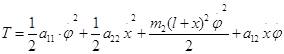
![]()
![]()
![]()
В положении равновесия:
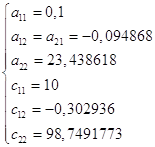 (3.2.1)
(3.2.1)
Запишем дифференциальные уравнения малых колебаний механической системы:
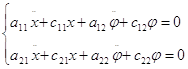
Составим характеристическое уравнение:

Или в развернутом виде:
![]()
Найдем корни характеристического уравнения, подставляя в уравнение найденные значения обобщенных коэффициентов инерции и жесткости:
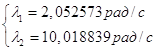
Определим коэффициенты форм колебаний:
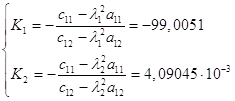
Таким образом, движение рассматриваемой системы при собственных колебаниях будет происходить по следующему закону:
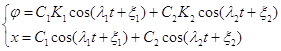 (3.2.2)
(3.2.2)
3.3Уравнения движения материальной точки и твердого тела при колебаниях
Найдем значения постоянных интегрирования ![]() системы уравнений (3.2.2) для следующих начальных условий:
системы уравнений (3.2.2) для следующих начальных условий:
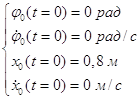

Решая систему уравнений, получим:
![]()
![]()
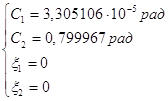
С учетом полученных значений постоянных интегрирования запишем окончательный вид уравнений колебаний:
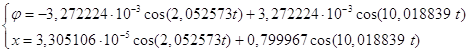
Список использованной литературы
1. Авраменко А.А., Архипов В.В., Асланов В.С., Тимбай И.А. Динамика точки и механической системы. – Самара: СГАУ. – 2001. – 84 с.
2. СТП СГАУ 6.1.4. – 97. Общие требования к оформлению учебных текстовых документов: методические указания.
Похожие работы
... в шарнире можно найти по формуле: , где и определяются выражениями (4.5) и (4.7); график её зависимости от времени приведён в приложении к курсовой работе (рис. 4). 5. Исследование движения механической системы с двумя степенями свободы с помощью уравнений Лагранжа II рода 5.1 Составление уравнений движения системы методом Лагранжа Уравнения второго рода являются одним из наиболее ...
... производные в уравнения Лагранжа (11): или (j=1,2,…, s). (12) Уравнения (12) называются уравнениями Лагранжа второго рода для консервативной системы. 7 Применение уравнений Лагранжа II рода к исследованию движения механической системы Массы тел механической системы m= 2m; m= 6m; m=m. Начальные условия:,,,. Найти уравнения движения системы в обобщенных координатах ,. Для ...
... груза, его скорости и ускорения, а также динамических реакций внешних и внутренних связей. Результаты расчетов: 5. Анализ результатов вычислений Математическая модель, описывающая поведение исследуемой механической системы, построена при следующих основных допущениях: ...
... и реакции внешних и внутренних связей. Произведен численный анализ полученного решения с использованием ЭВМ. Исходные данные: m = 1 кг r = 0.1 м с = 4000 H/м Часть 1. Применение основных теорем динамики механической системы 1.1 Постановка второй основной задачи динамики системы. Расчетная ...
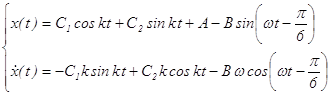
0 комментариев