Навигация
Поведение системы в конкретных условиях
2. Поведение системы в конкретных условиях
2.1 Дифференциальные уравнения движения системы и их интегрированиеСоставим уравнения движения с помощью уравнений Лагранжа 2-го рода. В выбранных обобщенных координатах ![]() и
и ![]() они принимают вид:
они принимают вид:
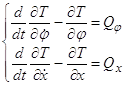 (2.1.1)
(2.1.1)
где ![]()
![]() - кинетическая энергия системы;
- кинетическая энергия системы;
![]() - обобщенные силы, соответствующие обобщенным координатам
- обобщенные силы, соответствующие обобщенным координатам ![]() и
и ![]() .
.
Найдем кинетическую энергию системы. Она состоит из кинетических энергий всех тел, входящих в систему:
![]()

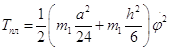
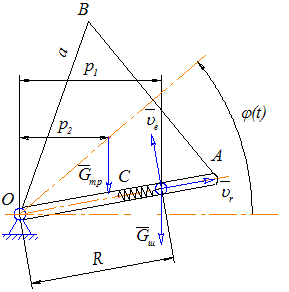
Абсолютная скорость шарика ![]() равна геометрической сумме относительной и переносной скоростей (см. рис. 3), ее величина определяется по формуле:
равна геометрической сумме относительной и переносной скоростей (см. рис. 3), ее величина определяется по формуле:


Тогда для кинетической энергии системы получим:
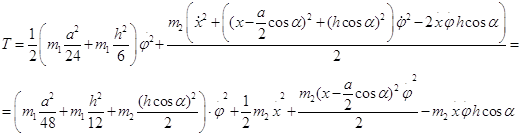 (2.1.2)
(2.1.2)
Введем обозначения:
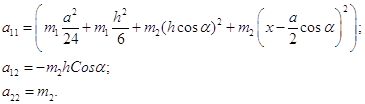
Найдем все производные левой части уравнений (2.1.3):
![]()
![]()
![]()
![]()
![]()
![]()
Обобщенные силы можно определить двумя способами:
1. Фиксируем координату ![]() , даем виртуальное перемещение
, даем виртуальное перемещение ![]() , находим элементарную работу:
, находим элементарную работу:
![]()
![]()
Фиксируем координату ![]() , даем виртуальное перемещение
, даем виртуальное перемещение ![]() , находим элементарную работу:
, находим элементарную работу:
![]()
![]()
2. Вычислим потенциальную энергию системы:
![]()
Найдем обобщенные силы:
![]()
![]()
![]()
Подставив производные левой части уравнений (2.1.1) и обобщенные силы ![]() и
и ![]() в уравнения (2.1.1), получим дифференциальные уравнения движения системы:
в уравнения (2.1.1), получим дифференциальные уравнения движения системы:
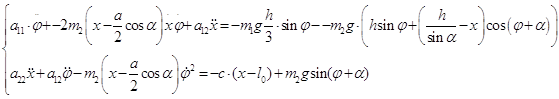
Для решения системы дифференциальных уравнений движения механической системы проведем численное интегрирование на ЭВМ. Результаты численного интегрирования приведены в приложении №2.
Для проверки численного интегрирования найдем, исходя из полученных данных, значения потенциальной и кинетической энергии механической системы. Суммируя значения потенциальной и кинетической энергии механической системы проверим, выполняется ли Закон сохранения энергии (см. приложение №2).
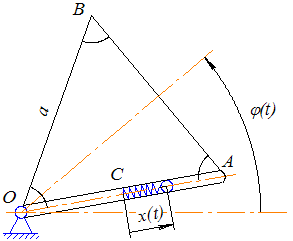
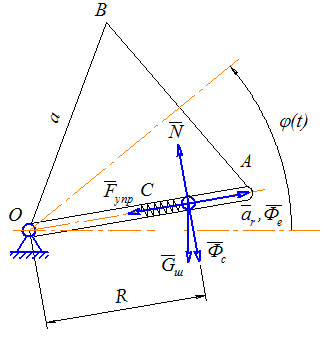
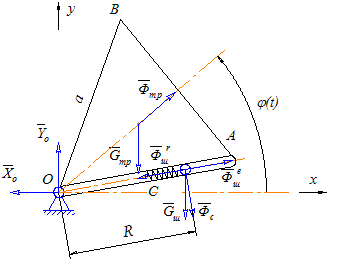
2.2 Определение реакций в опорах методом кинетостатикиВыберем для нашей системы неподвижную систему координат О1X1Y1, (cм. рис.4).

Рис.4. Силы, действующие на систему
Уравнения кинетостатики в векторной форме имеют вид
 (2.2.1)
(2.2.1)
где ![]() - главные векторы активных сил, реакций связей и сил инерции;
- главные векторы активных сил, реакций связей и сил инерции;
![]() - главные моменты активных сил, реакций связей и сил инерции относительно точки О1.
- главные моменты активных сил, реакций связей и сил инерции относительно точки О1.
Сила инерции шарика как материальной точки, совершающей сложное движение, равна геометрической сумме относительной, переносной и кориолисовой сил инерции:
![]()
![]() ,
,
![]()
Сила инерции пластины будет равна:
![]()
Модули сил инерции равны
![]() ,
, ![]() ,
, ![]()
![]() (2.2.2)
(2.2.2)
Изобразим активные силы, реакции опоры и силы инерции, действующие на механическую систему (рис. 4). Векторные уравнения кинетостатики (2.2.1) в проекциях на оси неподвижной системы координат OX1Y1 имеют вид
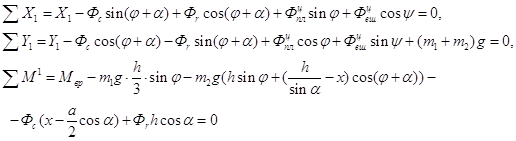 (2.2.3)
(2.2.3)
C учётом выражений для сил инерции (2.2.2), уравнения (2.2.3) принимают вид

Найденные уравнения реакций шарнира и вращательного момента совпадают с теми, что были найдены в предыдущих частях курсовой работы.
Похожие работы
... в шарнире можно найти по формуле: , где и определяются выражениями (4.5) и (4.7); график её зависимости от времени приведён в приложении к курсовой работе (рис. 4). 5. Исследование движения механической системы с двумя степенями свободы с помощью уравнений Лагранжа II рода 5.1 Составление уравнений движения системы методом Лагранжа Уравнения второго рода являются одним из наиболее ...
... производные в уравнения Лагранжа (11): или (j=1,2,…, s). (12) Уравнения (12) называются уравнениями Лагранжа второго рода для консервативной системы. 7 Применение уравнений Лагранжа II рода к исследованию движения механической системы Массы тел механической системы m= 2m; m= 6m; m=m. Начальные условия:,,,. Найти уравнения движения системы в обобщенных координатах ,. Для ...
... груза, его скорости и ускорения, а также динамических реакций внешних и внутренних связей. Результаты расчетов: 5. Анализ результатов вычислений Математическая модель, описывающая поведение исследуемой механической системы, построена при следующих основных допущениях: ...
... и реакции внешних и внутренних связей. Произведен численный анализ полученного решения с использованием ЭВМ. Исходные данные: m = 1 кг r = 0.1 м с = 4000 H/м Часть 1. Применение основных теорем динамики механической системы 1.1 Постановка второй основной задачи динамики системы. Расчетная ...
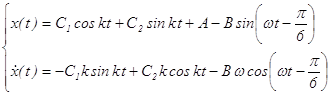
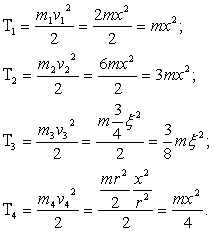
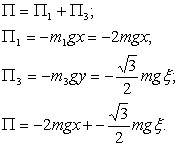
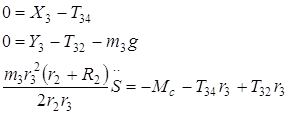
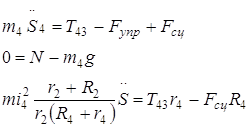
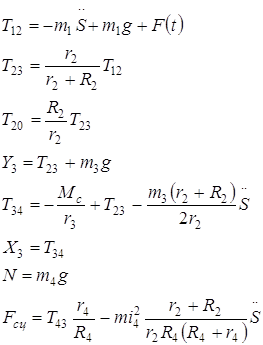
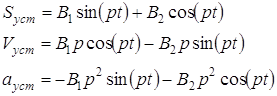
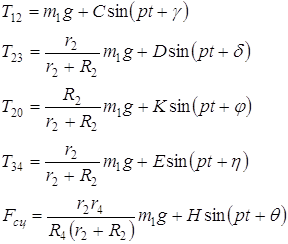
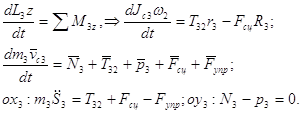
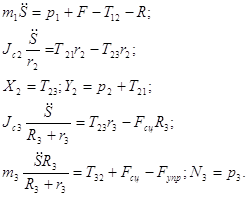
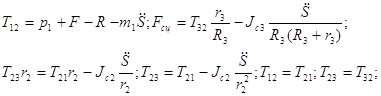
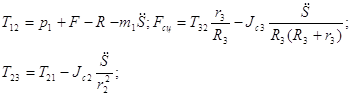
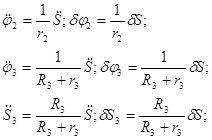
0 комментариев