Навигация
Еліптичні інтеграли 1-го, 2-го і 3-го роду
4. Еліптичні інтеграли 1-го, 2-го і 3-го роду
Тепер залишається вивчити найпростіші з інтегралів виду (8), до яких можна було б звести всі інтеграли цього виду, а відповідно, в кінцевому рахунку, і взагалі, всі еліптичні інтеграли.
Виділимо з раціональної функції R(x), що зустрічається в підінтегральному виразі (8) цілу частину P(x), а правильний дріб, який входить до його складу, розкладемо на прості дроби. Якщо не об’єднувати спряжені комплексні корені знаменника, а розглядати їх окремо, як дійсні корені, то R(x) представиться у вигляді суми степенів ![]() (n = 0, 1, 2,…) і дробів виду
(n = 0, 1, 2,…) і дробів виду 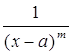 (m = 1, 2, 3,…), де а може бути і уявним числом, помножених на числові коефіцієнти. Звідси ясно, що інтеграл (8), в загальному випадку, являється лінійним агрегатом наступних інтегралів:
(m = 1, 2, 3,…), де а може бути і уявним числом, помножених на числові коефіцієнти. Звідси ясно, що інтеграл (8), в загальному випадку, являється лінійним агрегатом наступних інтегралів:
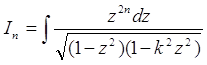 (n = 0, 1, 2,…)
(n = 0, 1, 2,…)
і![]()
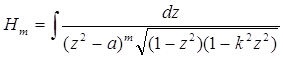 (m = 1, 2, 3,…).
(m = 1, 2, 3,…).
Зупинимося на інтегралах ![]() . Якщо проінтегрувати тотожність
. Якщо проінтегрувати тотожність
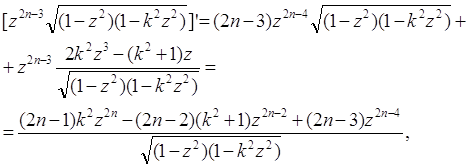
то отримаємо рекурентне співвідношення
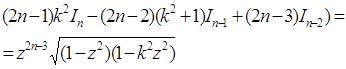 (9)
(9)
що зв’язують три послідовні інтеграли І. Припускаючи що тут n=2, виразимо ![]() через
через ![]() та
та ![]() ; якщо взяти n=3 і замість
; якщо взяти n=3 і замість ![]() підставити його вираз через
підставити його вираз через ![]() та
та ![]() , то навіть
, то навіть ![]() виразиться через ці інтеграли. Продовжуючи так далі, легко переконатися, що кожен з інтегралів
виразиться через ці інтеграли. Продовжуючи так далі, легко переконатися, що кожен з інтегралів ![]() виражається через
виражається через ![]() та
та ![]() і далі враховуючи (9), можна встановити і вигляд з’єднуючої їх формули
і далі враховуючи (9), можна встановити і вигляд з’єднуючої їх формули
![]()
де ![]() і
і ![]() - постійні, а
- постійні, а ![]() є непарний многочлен степені (2n-3). Звідси стає зрозумілим, що якщо
є непарний многочлен степені (2n-3). Звідси стає зрозумілим, що якщо ![]() є многочлен n – ї степені від х, то
є многочлен n – ї степені від х, то
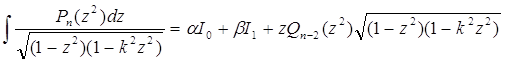 , (10)
, (10)
де ![]() і
і ![]() - постійні, а
- постійні, а ![]() (х) є деякий многочлен (n-2) – ї степені від х. Визначення цих постійних і коефіцієнтів многочлена Q може бути виконано (якщо многочлен Р коректно заданий за методом невизначених коефіцієнтів.)
(х) є деякий многочлен (n-2) – ї степені від х. Визначення цих постійних і коефіцієнтів многочлена Q може бути виконано (якщо многочлен Р коректно заданий за методом невизначених коефіцієнтів.)
Зауважимо, що з (9) можна було б виразити через ![]() та
та ![]() інтеграли
інтеграли ![]() і при від’ємних значеннях (n = -1, -2, …), так що в інтегралах
і при від’ємних значеннях (n = -1, -2, …), так що в інтегралах ![]() досить обмежитись випадком
досить обмежитись випадком ![]() .
.
Переходячи до інтегралів ![]() (скажімо, при дійсних a), подібним чином встановимо для них рекурентне співвідношення
(скажімо, при дійсних a), подібним чином встановимо для них рекурентне співвідношення
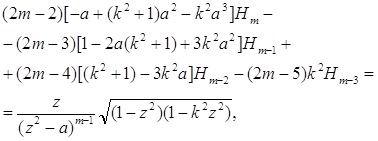
справедливе і при від’ємних і нульовому значеннях m.
Звідси всі ![]() виражаються через три з них:
виражаються через три з них:
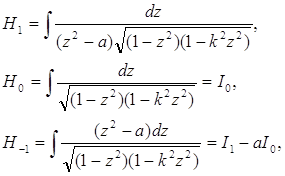
тобто, кінцево через ![]() ,
, ![]() та
та ![]() .
.
Підкреслимо, що усе це зберігає силу і при уявних значеннях параметра а.
Так в результаті усіх наших тверджень ми підходимо до наступних висновків: всі еліптичні інтеграли за допомогою елементарних підстановок – з точністю до доданків, що виражаються в кінцевому виді, - приводяться до наступних трьох стандартних інтегралів:
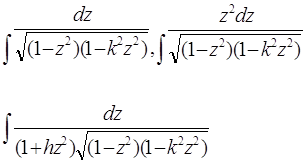
|
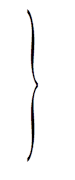
( останній інтеграл виходить із ![]() введенням, замість
введенням, замість ![]() , нового параметра
, нового параметра 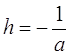 ). Ці інтеграли, як показав Ліувіль , в кінцевому виді вже не беруться. Лежандр їх назвав еліптичними інтегралами, відповідно, 1-го, 2-го і 3-го роду. Перші два містять лише один параметр k, а останній, крім нього, ще (комплексний) параметр h.
). Ці інтеграли, як показав Ліувіль , в кінцевому виді вже не беруться. Лежандр їх назвав еліптичними інтегралами, відповідно, 1-го, 2-го і 3-го роду. Перші два містять лише один параметр k, а останній, крім нього, ще (комплексний) параметр h.
Лежандр вніс у ці інтеграли ще подальші спрощення, виконавши в них підстановку ![]() (
(![]() змінюється від 0 до
змінюється від 0 до ![]() ). При цьому перший із них безпосередньо переходить в інтеграл
). При цьому перший із них безпосередньо переходить в інтеграл
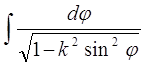 . (11)
. (11)
Другий перетворюється так:
![]()
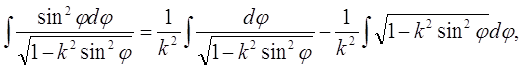
тобто приводиться до попереднього інтеграла і до нового інтеграла
![]() . (12)
. (12)
Нарешті, третій інтеграл при вказаній підстановці переходить в
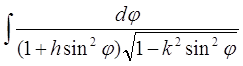 . (13)
. (13)
Інтеграли (11), (12) і (13) також називаються еліптичними інтегралами 1-го, 2-го і 3-го роду – в формі Лежандра.
Із них особливо важливе значення і застосування мають перші два. Якщо враховувати, що ці інтеграли при ![]() перетворюються в нуль, і тим зафіксувати вільні сталі, що містяться в них, то отримаємо дві доволі визначені функції від
перетворюються в нуль, і тим зафіксувати вільні сталі, що містяться в них, то отримаємо дві доволі визначені функції від ![]() , які Лежандр позначив відповідно через F(k, φ) і E(k, φ). Тут, крім незалежної змінної
, які Лежандр позначив відповідно через F(k, φ) і E(k, φ). Тут, крім незалежної змінної ![]() , вказаний також параметр k, що називається модулем, який входить у вирази цих функцій.
, вказаний також параметр k, що називається модулем, який входить у вирази цих функцій.
Лежандром були складені обширні таблиці значень цих функцій при різних ![]() і різних k. В них не тільки аргумент
і різних k. В них не тільки аргумент ![]() ,який трактуються як кут, що виражається в градусах, але і модуль k розглядається як синус деякого кута
,який трактуються як кут, що виражається в градусах, але і модуль k розглядається як синус деякого кута![]() , який і вказується в таблиці замість модуля, причому також в градусах.
, який і вказується в таблиці замість модуля, причому також в градусах.
Крім того, як Лежандром, так і іншими вченими були вивчені найглибші властивості цих функцій, встановлений ряд формул, що відносяться до них, і т.д.
Дякуючи цьому функції F і E Лежандра ввійшли в сім’ю функцій, що зустрічаються в аналізі і його додатках, на рівних правах з елементарними функціями.
Висновки
В результаті усіх наших міркувань ми коротко можемо сказати, що всі еліптичні інтеграли за допомогою елементарних підстановок – з точністю до доданків, що виражаються в кінцевому виді, - приводяться до наступних трьох стандартних інтегралів Лежандра:
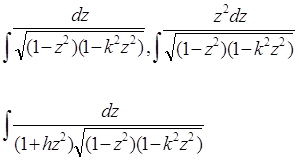
|
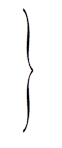
А за допомогою підстановки ![]() (
(![]() змінюється від 0 до
змінюється від 0 до ![]() ) ці інтеграли перетворюються в такі:
) ці інтеграли перетворюються в такі:
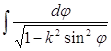 ,
, ![]() і
і 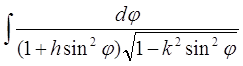 ,
,
які також називаються еліптичними інтегралами 1-го, 2-го і 3-го роду в формі Лежандра, значення яких можна знайти в таблицях.
Використана література:
1. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Том I. М.: Наука, 1966 г., 800 стр. с илл.
2. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Том II. М.: Наука, 1966 г., 800 стр. с илл.
3. Г. Корн, Т. Корн. Справочник по математике для научных работников и инженеров. М.: Наука, 1973 г., 832 стр. с илл.
4. И.Н. Бронштейн, К.А. Семендяев. Справочник по математике для инженеров и учащихся вузов. М.: Наука, 1980 г., 976 с., илл.
ДОДАТКИ Еліптичні інтеграли першого роду
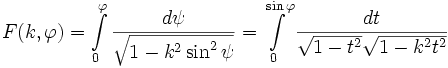
| Еліптичні інтеграли першого роду | ||||||||||
| 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° | |
| 0° | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 10 | 0.1745 | 0.1746 | 0.1746 | 0.1748 | 0.1749 | 0.1751 | 0.1752 | 0.1753 | 0.1754 | 0.1754 |
| 20 | 0.3491 | 0.3493 | 0.3499 | 0.3508 | 0.3520 | 0.3533 | 0.3545 | 0.3555 | 0.3561 | 0.3564 |
| 30 | 0.5236 | 0.5243 | 0.5263 | 0.5294 | 0.5334 | 0.5379 | 0.5422 | 0.5459 | 0.5484 | 0.5493 |
| 40 | 0.6981 | 0.6997 | 0.7043 | 0.7116 | 0.7213 | 0.7323 | 0.7436 | 0.7535 | 0.7604 | 0.7629 |
| 50 | 0.8727 | 0.8756 | 0.8842 | 0.8982 | 0.9173 | 0.9401 | 0.9647 | 0.9876 | 1.0044 | 1.0107 |
| 60 | 1.0472 | 1.0519 | 1.0660 | 1.0896 | 1.1226 | 1.1643 | 1.2126 | 1.2619 | 1.3014 | 1.3170 |
| 70 | 1.2217 | 1.2286 | 1.2495 | 1.2853 | 1.3372 | 1.4068 | 1.4944 | 1.5959 | 1.6918 | 1.7354 |
| 80 | 1.3963 | 1.4056 | 1.4344 | 1.4846 | 1.5597 | 1.6660 | 1.8125 | 2.0119 | 2.2653 | 2.4362 |
| 90 | 1.5708 | 1.5828 | 1.6200 | 1.6858 | 1.7868 | 1.9356 | 2.1565 | 2.5046 | 3.1534 |
|
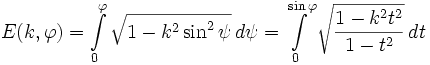
| Еліптичні інтеграли другого роду | ||||||||||
| 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° | |
| 0° | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 10 | 0.1745 | 0.1745 | 0.1744 | 0.1743 | 0.1742 | 0.1740 | 0.1739 | 0.1738 | 0.1737 | 0.1736 |
| 20 | 0.3491 | 0.3489 | 0.3483 | 0.3473 | 0.3462 | 0.3450 | 0.3438 | 0.3429 | 0.3422 | 0.3420 |
| 30 | 0.5236 | 0.5229 | 0.5209 | 0.5179 | 0.5141 | 0.5100 | 0.5061 | 0.5029 | 0.5007 | 0.5000 |
| 40 | 0.6981 | 0.6966 | 0.6921 | 0.6851 | 0.6763 | 0.6667 | 0.6575 | 0.6497 | 0.6446 | 0.6428 |
| 50 | 0.8727 | 0.8698 | 0.8614 | 0.8483 | 0.8317 | 0.8134 | 0.7954 | 0.7801 | 0.7697 | 0.7660 |
| 60 | 1.0472 | 1.0426 | 1.0290 | 1.0076 | 0.9801 | 0.9493 | 0.9184 | 0.8914 | 0.8728 | 0.8660 |
| 70 | 1.2217 | 1.2149 | 1.1949 | 1.1632 | 1.1221 | 1.0750 | 1.0266 | 0.9830 | 0.9514 | 0.9397 |
| 80 | 1.3963 | 1.3870 | 1.3597 | 1.3161 | 1.2590 | 1.1926 | 1.1225 | 1.0565 | 1.0054 | 0.9848 |
| 90 | 1.5708 | 1.5589 | 1.5238 | 1.4675 | 1.3931 | 1.3055 | 1.2111 | 1.1184 | 1.0401 | 1.0000 |
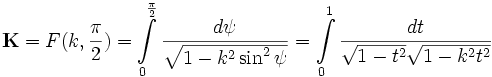
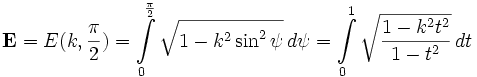
| Повні еліптичні інтеграли | ||||||||
|
|
|
|
|
|
|
|
|
|
| 0 | 1.5708 | 1.5708 | 30 | 1.6858 | 1.4675 | 60 | 2.1565 | 1.2111 |
| 1 | 1.5709 | 1.5707 | 31 | 1.6941 | 1.4608 | 61 | 2.1842 | 1.2015 |
| 2 | 1.5713 | 1.5703 | 32 | 1.7028 | 1.4539 | 62 | 2.2132 | 1.1920 |
| 3 | 1.5719 | 1.5697 | 33 | 1.7119 | 1.4469 | 63 | 2.2435 | 1.1826 |
| 4 | 1.5727 | 1.5689 | 34 | 1.7214 | 1.4397 | 64 | 2.2754 | 1.1732 |
| 5 | 1.5738 | 1.5678 | 35 | 1.7312 | 1.4323 | 65 | 2.3088 | 1.1638 |
| 6 | 1.5751 | 1.5665 | 36 | 1.7415 | 1.4248 | 66 | 2.3439 | 1.1545 |
| 7 | 1.5767 | 1.5649 | 37 | 1.7522 | 1.4171 | 67 | 2.3809 | 1.1453 |
| 8 | 1.5785 | 1.5632 | 38 | 1.7633 | 1.4092 | 68 | 2.4198 | 1.1362 |
| 9 | 1.5805 | 1.5611 | 39 | 1.7748 | 1.4013 | 69 | 2.4610 | 1.1272 |
| 10 | 1.5828 | 1.5589 | 40 | 1.7868 | 1.3931 | 70 | 2.5046 | 1.1184 |
| 11 | 1.5854 | 1.5564 | 41 | 1.7992 | 1.3849 | 71 | 2.5507 | 1.1096 |
| 12 | 1.5882 | 1.5537 | 42 | 1.8122 | 1.3765 | 72 | 2.5998 | 1.1011 |
| 13 | 1.5913 | 1.5507 | 43 | 1.8256 | 1.3680 | 73 | 2.6521 | 1.0927 |
| 14 | 1.5946 | 1.5476 | 44 | 1.8396 | 1.3594 | 74 | 2.7081 | 1.0844 |
| 15 | 1.5981 | 1.5442 | 45 | 1.8541 | 1.3506 | 75 | 2.7681 | 1.0764 |
| 16 | 1.6020 | 1.5405 | 46 | 1.8691 | 1.3418 | 76 | 2.8327 | 1.0686 |
| 17 | 1.6061 | 1.5367 | 47 | 1.8848 | 1.3329 | 77 | 2.9026 | 1.0611 |
| 18 | 1.6105 | 1.5326 | 48 | 1.9011 | 1.3238 | 78 | 2.9786 | 1.0538 |
| 19 | 1.6151 | 1.5283 | 49 | 1.9180 | 1.3147 | 79 | 3.0617 | 1.0468 |
| 20 | 1.6200 | 1.5238 | 50 | 1.9356 | 1.3055 | 80 | 3.1534 | 1.0401 |
| 21 | 1.6252 | 1.5191 | 51 | 1.9539 | 1.2963 | 81 | 3.2553 | 1.0338 |
| 22 | 1.6307 | 1.5141 | 52 | 1.9729 | 1.2870 | 82 | 3.3699 | 1.0278 |
| 23 | 1.6365 | 1.5090 | 53 | 1.9927 | 1.2776 | 83 | 3.5004 | 1.0223 |
| 24 | 1.6426 | 1.5037 | 54 | 2.0133 | 1.2681 | 84 | 3.6519 | 1.0172 |
| 25 | 1.6490 | 1.4981 | 55 | 2.0347 | 1.2587 | 85 | 3.8317 | 1.0127 |
| 26 | 1.6557 | 1.4924 | 56 | 2.0571 | 1.2492 | 86 | 4.0528 | 1.0086 |
| 27 | 1.6627 | 1.4864 | 57 | 2.0804 | 1.2397 | 87 | 4.3387 | 1.0053 |
| 28 | 1.6701 | 1.4803 | 58 | 2.1047 | 1.2301 | 88 | 4.7427 | 1.0026 |
| 29 | 1.6777 | 1.4740 | 59 | 2.1300 | 1.2206 | 89 | 5.4349 | 1.0008 |
| 30 | 1.6858 | 1.4675 | 60 | 2.1565 | 1.2111 | 90 |
| 1.0000 |
Похожие работы
... . Тоді, якщо існує скінченна границя (13), її називають невласним інтегралом першого роду і позначають так: (14) Таким чином, за означенням (15) У цьому випадку інтеграл (14) називають збіжним, а підінтегральну функцію f(x) – інтегрованою на проміжку (а;+). Якщо ж границя (13) не існує або нескінченна, то інтеграл (14) називають також невласним але розбіжним, а функція f(x) – ...
... на малому , g(x,y) стала y1 = y(x0 ) + y(x0 ) + g(x0, y0 ) x Повторюючи знайдемо y2 = y(x1+x) y(x1) + g(x1, y1 ) x yn= yn-1+ g(xn-1 ,yn-1) x, (n=0,1,2…) нахил дотичної визначається початковою точкою інтервалу. 2.3. Програма для комп’ютера. Алгоритм методу. 1. Вибирається початкова умова, величина кроку і кількість ітерацій (кроків). 2. Визначається y і нахил у початковій точці ...
... метод координат. V. Аксіома паралельності Сама остання аксіома грає в геометрії особливу роль, визначаючи поділ геометрії на дві логічно несуперечливі й взаємно виключають один одного системи: Евклідову й неевклідову геометрії. У геометрії Евкліда ця аксіома формулюється так. V. Нехай а – довільна пряма й А – крапка, що лежить поза прямій а, тоді в площині α, обумовленою крапкою А и ...
... для систем, частинок з антисиметричними хвильовими функціями, тобто до ферміонів. 2.2.3. Розподіл електронів за станами. Періодична система елементів. Сукупність електронів, які перебувають у всіх можливих станах з однаковим значенням головного квантового числа n, утворює електронну оболонку (електронний шар). Енергетичні шари прийнято позначати великими латинськими літерами відповідно до ...


0 комментариев