Навигация
Для матриці A знайти обернену матрицю
1. Для матриці A знайти обернену матрицю.
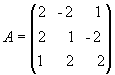
Рішення. Знаходимо спочатку детермінант матриці А:
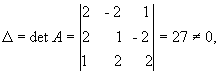
Це означає, що обернена матриця існує і ми її можемо знайти по формулі 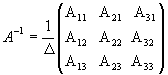 , де Аij (i,j=1,2,3) - алгебраїчні доповнення до елементів аijпочаткової матриці.
, де Аij (i,j=1,2,3) - алгебраїчні доповнення до елементів аijпочаткової матриці.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
звідки 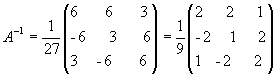 .
.
2. Знайти матрицю, обернену до матриці.
A = 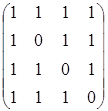
Знаходимо спочатку визначник матриці A:
![]()
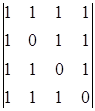 =
= 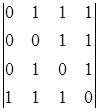 = 1
= 1![]() (-1)4+1
(-1)4+1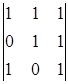 = (-1)
= (-1)![]()
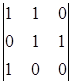 =
=
= (-1)![]() 1
1![]() (-1)3+1
(-1)3+1![]() = -1
= -1 ![]() 0. Отже обернена матриця існує.
0. Отже обернена матриця існує.
Знаходимо алгебраїчні доповнення:
A11=(-1)1+1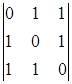 = 2 A21=(-1)2+1
= 2 A21=(-1)2+1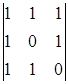 = -1
= -1
A31=(-1)3+1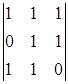 = -1 A41=(-1)4+1
= -1 A41=(-1)4+1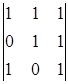 = -1
= -1
A12=(-1)1+2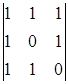 = -1 A22=(-1)2+2
= -1 A22=(-1)2+2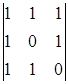 = 1
= 1
A32=(-1)3+2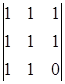 = 0 A42=(-1)4+2
= 0 A42=(-1)4+2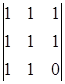 = 0
= 0
A13=(-1)1+3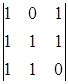 = -1 A23=(-1)2+3
= -1 A23=(-1)2+3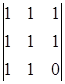 = 0
= 0
A33=(-1)3+3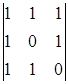 = 1 A43=(-1)4+3
= 1 A43=(-1)4+3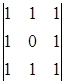 = 0
= 0
A14=(-1)1+4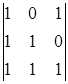 = -1 A24=(-1)2+4
= -1 A24=(-1)2+4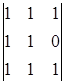 = 0
= 0
A34=(-1)3+4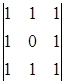 = 0 A44=(-1)4+4
= 0 A44=(-1)4+4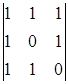 = 1
= 1
Підставляючи у формулу (3) знайдені значення, одержуємо:
A-1 = 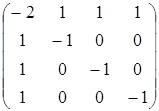
Перевірка. Одержаний результат можна легко перевірити.
Оскільки, AA-1 = E, де E –це одинична матриця, то:
A![]() A-1 =
A-1 = 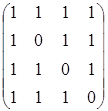
![]()
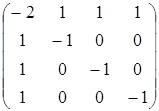 =
=
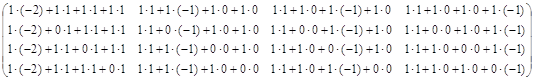 =
=
= 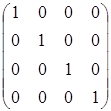
Отже, обернену матрицю знайдено вірно.
Висновки
Отже, висвітливши основні поняття обернених матриць, можна прийти до висновку, що процес знаходження обернених матриць за допомогою формули є швидким і простим методом аналізу стану певного об’єкта.
Список використаної літератури
1. Ващук Ф.Г., Поляк С.С. Практикум з вищої математики. - Ужгород, 2005. 6 – 24 с.
2. Курош А.Г. Курс высшей алгебры. - Москва, 1968. 95–99 с.
Додаток
Дану задачу можна реалізувати на мові програмування Turbo Pascal
Лістінг програми
Program InversMatrix;
const max_size=10; {max size matrix }
type matr=array[1..max_size,1..max_size] of real;
label 1;
var
a,invers,tmp_matrix : matr;
size : Integer; {size matrix}
i,j :Integer;
dt : real;
procedure PrintMatr(m:matr;n:integer);
var i,j:integer;
begin
for i:=1 to n do
begin
for j:=1 to n do
write(m[i,j]:8:3);
writeln;
end;
end;
Function Pow (x:Integer; y:Integer):Integer;
var
i,z :Integer;
begin
z := 1;
for i:=1 to y do
z := z * x;
Pow := z;
end;
procedure GetMatr(a:matr; var b:matr; m,i,j:integer);
var ki,kj,di,dj:integer;
begin
di:=0;
for ki:=1 to m-1 do
begin
if (ki=i) then di:=1;
dj:=0;
for kj:=1 to m-1 do
begin
if (kj=j) then dj:=1;
b[ki,kj]:=a[ki+di,kj+dj];
end;
end;
end;
Function Determinant(a:matr;n:integer):real;
var i,j,k:longint;
b:matr;
d : real;
begin
d:=0; k:=1;
if (n<1) then
begin
writeln('Determinant: Cann''t run. N=',n); halt;
end;
if (n=1)
then d:=a[1,1]
else if (n=2)
then d:=a[1,1]*a[2,2]-a[2,1]*a[1,2]
else { n>2 }
for i:=1 to n do
begin
GetMatr(a,b,n,i,1);
{writeln('i=',i,' a[',i,',1]=',a[i,1]);
PrintMatr(b,n-1);}
d:=d+k*a[i,1]*Determinant(b,n-1);
k:=-k;
end;
Determinant:=d;
end;
begin
Write('Enter size matrix [1..10] :');
ReadLn(size);
for i:=1 to size do
for j:=1 to size do
begin
Write('a[',i,',',j,']=');
ReadLn(a[i,j]);end;
begin
if determinant(a,size)=0 then
begin write ('matryca vyrudzena,obernenoi ne isnue!');
goto 1; end;
end;
WriteLn('================================================');
WriteLn(' Source matrix ');
WriteLn;
PrintMatr(a,size);
dt:=Determinant(a,size);
WriteLn('================================================');
writeln('Determinant = ',dt:8:3);
{sozdaem matrix is dopolneniy}
for i:=1 to size do
for j:=1 to size do
begin
GetMatr(a,tmp_matrix,size,j,i);
invers[i,j]:=Pow(-1,i+j)*Determinant(tmp_matrix,size-1)/dt;
end;
WriteLn('================================================');
WriteLn(' Inverse matrix ');
WriteLn;
PrintMatr(invers,size);
1:readln;
end.
Контрольні приклади
Приклад 1.
Вхідні дані –
Розмірність матриці – 3
1 2 3 -2.00 4.00 -1.00
1 1 2 → обернена матриця→ 0.00 -1.00 0.00
1 0 2 1.00 -2.00 1.00
Приклад 2.
Вхідні дані –
Розмірність матриці – 4
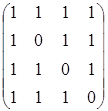 обернена матриця
обернена матриця 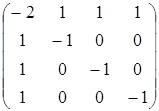
Похожие работы
... у загальному випадку різними. 2. Опис програми Програма Matrtest. pas являється демо программою, котра показує роботу процедур з модуля Matr. pas. Модуль програми Matr. pas – в ній розміщені процедури і функції, котрі роблять перетворення матриць. У файлі – Time. dat записані коефіціенти матриці, розмірність матриці. Він мусить містити в собі початкову матрицю, і її розмірність, тому, ...
... Звідси . Власний вектор можна обчислити з умов ортогональності: Звідси Або Після нормування остаточно отримаємо: 2.6 приклади задач, що зводяться до відшукання власних значень та власних векторів матриці Задача 1 Дослідимо тривісне напруження стану елемента тіла, представленого на малюнку. Матриця напруги для нього має вигляд Якщо ...
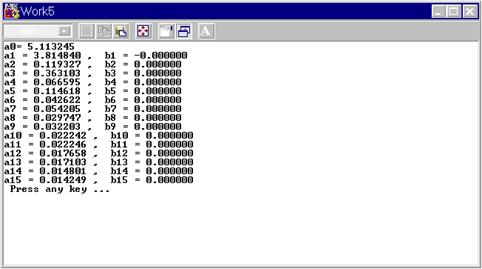
... чного сплайну. ; . Для знаходження коефіцієнті вкубічного сплайну призначена програма Work2_2. //------------------------------------------------------------ // Work2_2.cpp //------------------------------------------------------------ // "Числові методи" // Завдання 2 // Інтерполювання функції кубічним сплайном #include <stdio.h> #include <iostream.h> #include <conio ...
... ів рядка (стовпця) відповідних елементів іншого рядка (стовпця); 5) вилучення нульового рядка (стовпця); 6) викреслення рядка (стовпця), що є лінійною комбінацією інших рядків (стовпців). Однорідні системи. Розглядається однорідна система лінійних рівнянь з n невідомими: Ах = 0. Якщо rangА = n (detА ¹ 0), то система визначена і має тільки тривіальний розв’язок: x1 = x2 = … = xn = 0. Якщо ...

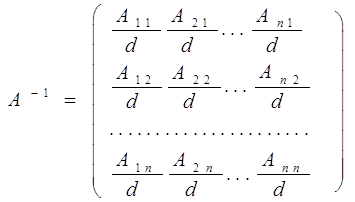
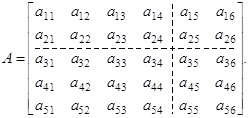
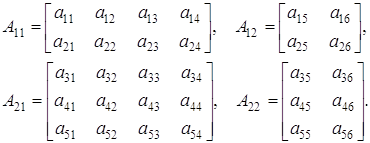
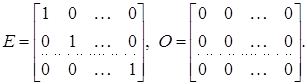
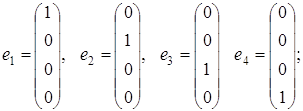
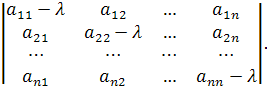
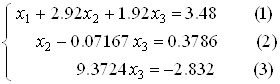
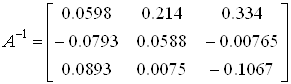
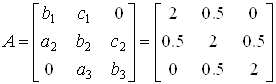


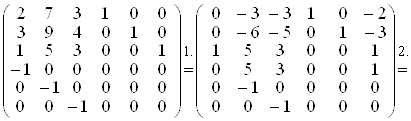
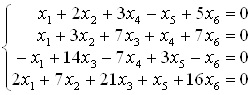
0 комментариев