Навигация
Власні значення і власні вектори матриці
Міністерство освіти і науки України
Криворізький державний педагогічний університет
Кафедра математики
Курсова робота з математики
Власні значення і власні вектори матриці
Студента ІV курсу фізико-математичного факультету
Палія Валерія Миколайовича
Науковий керівник
ст. викладач Корольська Л. Р.
Кривий Ріг
2009 р.
ЗМІСТ
Вступ
Розділ І. Основні відомості з лінійної алгебри
1.1 Види матриць. Дії над матрицями. Визначник
1.2 Власні значення та власні вектори матриці
Розділ ІІ. Знаходження власних векторів і власних значень матриць
2.1 Метод А. М. Данілевського
2.2 Метод А. Н. Крилова
2.3 Метод Леверрьє
2.4 Метод невизначених коефіцієнтів
2.5 Метод скалярних добутків для знаходження першого власного значення дійсної матриці
2.6 приклади задач, що зводяться до відшукання власних значень та власних векторів матриці
Висновки
Список використаних джерел
Вступ
Історично першим розділом лінійної алгебри був розділ теорії лінійних рівнянь. Згодом у зв’язку з розв’язанням системи лінійних рівнянь було введено поняття "визначник" в 1750 році Крамером. У зв’язку з вивченням лінійних рівнянь та визначників вводиться поняття матриці в 1877 році Г. Фробеніусом. В кінці 19 століття з’явився новий розділ лінійної алгебри "Власні значення та власні вектори матриць". Цей розділ має прикладне значення.
Як з’ясувалося, деякі спеціалісти донині цікавляться такою проблемою лінійної алгебри, як обчислення власних значень та власних векторів матриць. Ця проблема виникає в багатьох областях математики, механіки, інженерної справи та геології.
Актуальність нашого дослідження полягає втому, що цілий ряд| інженерних задач зводиться до розгляду систем рівнянь, що мають єдиний розв’язок лише в тому випадку, коли| відоме значення деякого вхідного в них параметра. Цей особливий параметр називається характеристичним, або власним, значенням системи. Із задачами на власні значення інженер стикається в різних ситуаціях. Так, для тензорів напруги власні значення визначає головна нормальна напруга, а власними векторами задаються напрями, пов'язані з цими значеннями. При динамічному аналізі механічних систем власні значення відповідають власним частотам коливань, а власні вектори характеризують моди цих коливань. При розрахунку конструкцій власні значення дозволяють визначати критичні навантаження, перевищення яких приводить до втрати стійкості. Вибір найбільш ефективного методу обчислення власних значень або власних векторів для даної інженерної задачі залежить від ряду чинників, таких, як тип рівнянь, число шуканих власних значень і їх характер.
Об’єктом нашого дослідження є елементи лінійної алгебри.
Предмет дослідження: методи знаходження власних значень і власних векторів матриць.
Задачі дослідження:
1) Аналіз навчальної та методичної літератури з теми дослідження.
2) Обгрунтувати методи знаходження власних векторів і власних значень матриць.
3) Навести приклади знаходження власних векторів і власних значень матриць.
Розділ І. Основні відомості з лінійної алгебри
1.1 Види матриць. Дії над матрицями. Визначник
Матрицею називається прямокутна таблиця з чисел, яка складається з деякої кількості m рядків та деякої кількості n стовпців.
Числа m і n називаються порядками матриці. У випадку, якщо m = n, матриця називається квадратною, а число m = n — її порядком. [2, стор. 10]
Щоб записати матрицю, виписують належним чином позначення її елементів та отриману таблицю беруть в дужки або обмежують подвійними лініями.
Таким чином, загальний вигляд матриці розмірності (m, n) буде таким
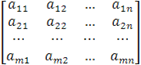 ,
, 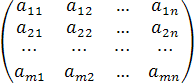 ,
, 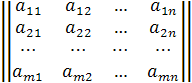 ,
,
де aij — позначення елементів з множини C. Часто замість такого докладного запису вживають скорочений: || aij || або || aij ||m,n.
Якщо кількість рядків матриці дорівнює кількості її стовпців, то матриця називається квадратною, а кількість її рядків, що дорівнює кількості стовпців, називається порядком квадратної матриці.
Матрицю, що має тільки один рядок, називають просто рядком матриці, а кількість його елементів — довжиною рядка. В подальшому матриці будуть позначатися великими літерами латинського алфавіту.
Дві матриці називаються рівними, якщо кількість рядків і стовпців у них відповідно рівні та якщо рівні числа, що стоять на відповідних місцях цих матриць. Таким чином, одна рівність між (m, n)-матрицями рівносильна системі mn рівностей між їх елементами.
Основними матричними операціями є множення числа на матрицю або матриці на число, додавання та перемноження двох матриць. За означенням, для того щоб помножити число α на матрицю А або матрицю А на число α, необхідно помножити α на всі елементи матриці А. Наприклад,
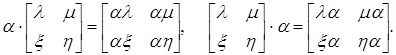
Матриця всі елементи якої дорівнюють нулю, називається нульовою матрицею і позначається О. Якщо бажають вказати явно кількість рядків і стовпців нульової матриці, то пишуть Оmn.
Блочні матриці. Припустимо, що деяка матриця ![]() за допомогою горизонтальних і вертикальних прямих розбита на окремі прямокутні клітини, кожна з яких являє собою матрицю менших розмірів і називається блоком вихідної матриці. В такому разі виникає можливість розгляду вихідної матриці А як деякої нової (так званої блочної) матриці
за допомогою горизонтальних і вертикальних прямих розбита на окремі прямокутні клітини, кожна з яких являє собою матрицю менших розмірів і називається блоком вихідної матриці. В такому разі виникає можливість розгляду вихідної матриці А як деякої нової (так званої блочної) матриці ![]() , елементами
, елементами ![]() слугують вказані блоки.
слугують вказані блоки.
Наприклад, матрицю
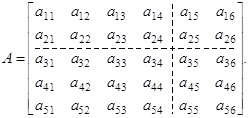
можна розглядати як блочну матрицю ![]() , елементами якої слугують наступні блоки:
, елементами якої слугують наступні блоки:
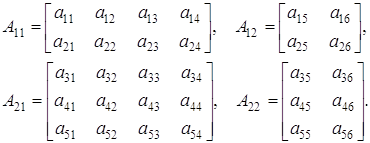
Цікавим є той факт, що основні операції з блочними матрицями здійснюються за тими ж правилами, по яким вони здійснюються зі звичайними числовими матрицями, тільки в ролі елементів виступають блоки. [2, стор. 15]
Для довільної матриці А та довільних α, β мають місце такі співввідношення:
1. ![]()
2. ![]()
3. ![]()
Сумою двох матриць А і В, що мають відповідно рівну кількість рядків і стовпців, називається матриця, що має ту ж кількість рядків і стовпців і елементи, які дорівнюють сумам відповідних елементів матриць А, В. Наприклад,
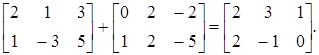
З цього визначення витікають співвідношення:
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
Вводячи позначення ![]() , будемо також мати
, будемо також мати
![]() [4]
[4]
Добутком матриці ![]() , що має відповідно розмірність m х n, на матрицю
, що має відповідно розмірність m х n, на матрицю ![]() , що має відповідно розмірність n х p, називається матриця
, що має відповідно розмірність n х p, називається матриця ![]() , що має відповідно розмірність m х p,та елементи
, що має відповідно розмірність m х p,та елементи ![]() , які визначаються за формулою
, які визначаються за формулою
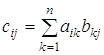
![]() (1)
(1)
Для позначення добутку матриці А на матрицю В використовують запис ![]() . Операція складання добутку матриці А на матрицю В називається перемноженням цих матриць.
. Операція складання добутку матриці А на матрицю В називається перемноженням цих матриць.
Зі сформульованого вище слідує, що матрицю А можна помножити не на будь-яку матрицю В: необхідно, щоб кількість стовпців матриці А дорівнювало кількості рядків матриці В.
Зокрема, два добутки ![]() можна визначити лише в тому випадку, коли кількість стовпців А співпадає з числом рядків В, а кількість рядків А співпадає з кількістю стовпців В. При цьому обидві матриці
можна визначити лише в тому випадку, коли кількість стовпців А співпадає з числом рядків В, а кількість рядків А співпадає з кількістю стовпців В. При цьому обидві матриці ![]() будуть квадратними, але порядки їх будуть різними. Для того щоб обидва добутки
будуть квадратними, але порядки їх будуть різними. Для того щоб обидва добутки ![]() не тільки були визначеними, але й мали однаковий порядок, необхідно і достатньо, щоб обидві матриці А і В були квадратними матрицями одного й того ж порядку.
не тільки були визначеними, але й мали однаковий порядок, необхідно і достатньо, щоб обидві матриці А і В були квадратними матрицями одного й того ж порядку.
Формула (1) являє собою правило складання елементів матриці С, що являє собою добуток матриці А на матрицю В. Це правило можна сформулювати і словесно: елемент ![]() , що стоїть на перетині і-го рядка та j-го стовпця матриці
, що стоїть на перетині і-го рядка та j-го стовпця матриці ![]() , дорівнює сумі попарних добутків відповідних елементів і-го рядка матриці А та j-го стовпця матриці В.
, дорівнює сумі попарних добутків відповідних елементів і-го рядка матриці А та j-го стовпця матриці В.
В якості приклада застосування вказаного правила приведемо формулу перемноження квадратних матриць другого порядку
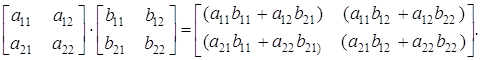
З формули (1) витікають наступні властивості добутку матриці А на матрицю В:
1. ![]()
2. ![]() або
або ![]()
Серед квадратних матриць виділимо клас так званих діагональних матриць, у кожної з яких елементи, що розташовані не на головній діагоналі, дорівнюють нулю. Кожна діагональна матриця має вид
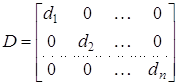 ,
,
де ![]() — які завгодно числа. Легко бачити, що якщо всі ці числа рівні між собою, тобто
— які завгодно числа. Легко бачити, що якщо всі ці числа рівні між собою, тобто ![]() то для будь-якої квадратної матриці А порядку n справедлива рівність
то для будь-якої квадратної матриці А порядку n справедлива рівність ![]() .
.
Серед усіх діагональних матриць, у яких діагональні елементи співпадають ![]() особливу роль відіграють дві матриці. Перша з них отримується при d = 1, називається одиничною матрицею n-го порядку і позначається Е. Друга матриця отримується при d = 0, називається нульовою матрицею n-го порядку і позначається О.
особливу роль відіграють дві матриці. Перша з них отримується при d = 1, називається одиничною матрицею n-го порядку і позначається Е. Друга матриця отримується при d = 0, називається нульовою матрицею n-го порядку і позначається О.
Таким чином,
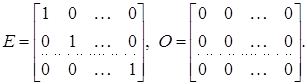
[2, стор. 14]
З правил дій над матрицями безпосередньо витікає, що сумма і добуток діагональних матриць буде знову діагональною матрицею:
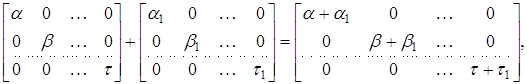
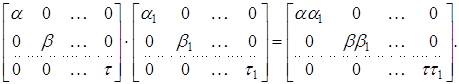
Розглянемо тепер довільну квадратну матрицю Х порядка п з елементами з кільця К. За означенням вважаємо
![]()
Оскільки при множені декількох матриць дужки можна розташовувати довільно, то для будь-яких цілих невід’ємних p, q та довільної матриці Х над асоціативним кільцем К маємо
![]() , (2)
, (2)
![]() .
.
Матриці А і В називаються переставними (комутативними), якщо
![]()
Зі співвідношення (2) отримаємо
![]() ,
,
і, значить, всі натуральні степені однієї і тієї ж матриці переставні між собою.
Справедливе й більш загальне твердження: якщо матриці А і В переставні, то будь-які їх натуральні степені також переставні й для будь-якого натурального p маємо
![]()
Транспонування матриць.
Розглянемо довільну матрицю
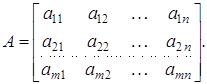
Матриця
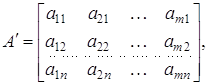
що отрималася з А заміною рядків стовпцями, називається транспонованою по відношенню до А.
Для довільних матриць А, В мають місце наступні правила транспонування:
![]() ,
,
![]()
де, α, β — довільні числа.
Якщо А — довільна квадратна матриця і
![]()
то А називається симетричною; якщо ж
![]()
то — кососиметричною. [4]
Поняття визначника. Розглянемо довільну квадратну матрицю будь-якого порядку n:
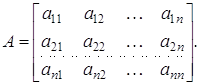
Визначник (або детермінант) визначається для довільної квадратної матриці А, і являє собою поліном від всіх її елементів. Позначається — або det(A), або — в розгорнутому вигляді
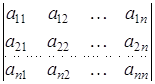
(матриця обмежується вертикальними лініями). Маючи на увазі порядок матриці А, про її визначник кажуть як про визначник порядку п.
Для п=1:
![]()
для п=2:
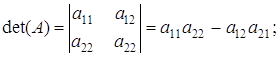
для п=3:
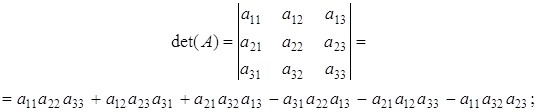
для п = 4 формула стає громіздкою.
Введемо тепер визначник довільного порядку п.
Впорядкована пара різних натуральних чисел (а,b) утворює інверсію (або порушення порядку), якщо ![]() . Будемо позначати число інверсій в парі (а,b) через
. Будемо позначати число інверсій в парі (а,b) через ![]() . Таким чином
. Таким чином
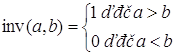
Число інверсій в послідовності різних натуральних чисел ![]() визначається наступним чином:
визначається наступним чином:
![]()
Визначником (або детермінантом) матриці
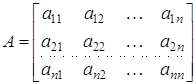
Називається
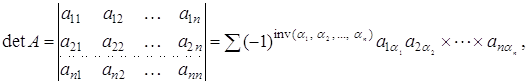
де сумма поширюється на всілякі перестановки ![]() елементів
елементів ![]() , Число п називається порядком визначника. В загальному випадку сума, що визначає детермінант порядку п, містить п! доданків, кожен з яких являє собою добуток п елементів визначника, взятих по одному з кожного рядка й з кожного стовпця (тобто після того, як в добуток вставляється елемент
, Число п називається порядком визначника. В загальному випадку сума, що визначає детермінант порядку п, містить п! доданків, кожен з яких являє собою добуток п елементів визначника, взятих по одному з кожного рядка й з кожного стовпця (тобто після того, як в добуток вставляється елемент ![]() більше в цей добуток не береться жодного елемента з j-го рядка та k-го стовпця). Знак в добутку визначається по вказаному вище правилу.
більше в цей добуток не береться жодного елемента з j-го рядка та k-го стовпця). Знак в добутку визначається по вказаному вище правилу.
Похожие работы
... і простору матриця лінійного оператора має діагональний вид, то всі вектори базису є власними векторами оператора . Таким чином, доведено наступне твердження. Теорема 5.2. Для того, щоб матриця лінійного оператора у базисі простору була діагональною, необхідно і достатньо, щоб вектори були власними векторами оператора . Теорема 5.3. Якщо власні значення лінійного оператора , діючого в -мі ...
... йний оператор задається матрицею . Отже, при зафіксованому базисі кожному лінійному оператору простору відповідає певна квадратна матриця -го порядку – матриця цього оператора. 3. Власні вектори й власні значення лінійного оператора Означення 1. Підпростір лінійного простору називається інваріантним відносно оператора , якщо , тобто якщо образ будь-якого вектора із міститься в . ...
... і означення Означення: Дифуром називається рівняння, яку містить шукану похідну ф-ії. Найбільший порядок похідних називається порядком диф.рівняння. Означення матрець, типи матрець. Означення: Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Їх позначають великими літерами A,B,C і т.д. Типи матрець: Квадратна матриця, в якої елементи головної діагоналі дорівнюють ...
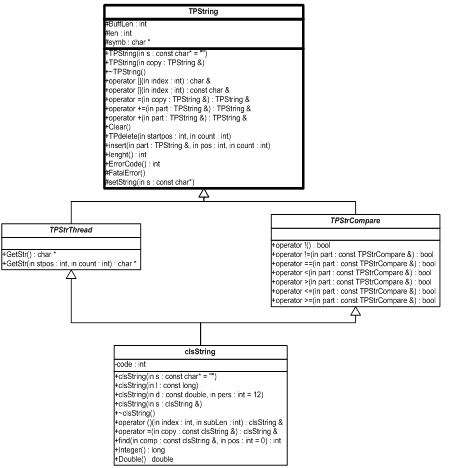
... ліворуч. Перевантажені операції помістити в потік і взяти з потоку повинні об’являтися як дружні, якщо вони повинні мати прямий доступ до закритих елементів класу з міркувань продуктивності. 2. Розробка власного класу clsString 2.1 Загальний алгоритм вирішення Створимо базовий клас TPString у якому розмістимо мінімальнонеобхідні компоненти, але при цьому цей клас вже буде функці ...




0 комментариев