Навигация
![]()
![]()
![]()
3 ч tвстр - ?
- Что еще известно в задаче? (Скорость товарного поезда 50 км/ч, скорость электропоезда 80 км/ч)
- Отметим эти данные на чертеже.
- Что нужно узнать? (Через сколько часов после своего выхода электропоезд догонит товарный поезд?)
- Обозначим неизвестное знаком вопроса.
- Известно, что товарный поезд шел 3 ч со скоростью 50 км/ч. Что можно узнать по этим данным? (Расстояние, которое пошел поезд за 3 ч)
- Что для этого нужно сделать? (Нужно скорость умножить на время)
- Зная скорость товарного поезда и электропоезда, что можно узнать? (Скорость сближения)
- Что для этого нужно сделать? (Нужно из скорости электропоезда вычесть скорость товарного поезда)
- Зная, сколько километров прошел товарный поезд и скорость сближения поездов, что можем найти? (Время, через которое встретятся поезда)
- Как можем это найти? (Расстояние разделить на скорость сближения)
- Записываем решение:
1) 50 ∙ 3 = 150 (км) – прошел товарный поезд.
2) 80 – 50 = 30 (км/ч) – скорость сближения.
3) 150 : 30 = 5 (ч) – через это время электропоезд догонит товарный поезд.
Ответ: через 5 часов.
Задача 4: (№ 1179)
«Два поезда вышли в разное время навстречу друг другу из двух городов, расстояние между которыми 782 км. Скорость первого поезда 52 км/ч, а второго 61 км/ч. Пройдя 416 км, первый поезд встретился со вторым. На сколько один из поездов вышел раньше другого?»
- Читаем внимательно задачу.
- Давайте к этой задаче составим чертеж.
- Что нам известно в задаче? (Два поезда вышли в разное время навстречу друг другу из двух городов)
- Отметим это на чертеже.
![]()
![]()
![]()
![]()
![]()
![]() 52 км/ч 61 км/ч
52 км/ч 61 км/ч

416 км
782 км
На сколько один из поездов вышел раньше другого?
- Что еще известно? (Расстояние между городами 782 км; скорость первого поезда 52 км/ч, а второго 61 км/ч)
- Отметим все данные на чертеже.
- Что нам еще дано? (Пройдя 416 км, первый поезд встретился со вторым)
- Покажем это на чертеже.
- Что нужно узнать в задаче? (На сколько один из поездов вышел раньше другого?)
- Можем сразу на него ответить? (Нет)
- Почему? (Не знаем, сколько часов ехал первый поезд)
- Можем это найти? (Да)
- Как? (Надо расстояние, которое прошел первый поезд, разделить на скорость)
- А сейчас можем ответить на главный вопрос? (Нет)
- Почему? (Сначала надо найти расстояние, которое прошел второй поезд)
- Можем найти это расстояние? (Да)
- Как найдем? (Нужно из расстояния между городами вычесть то расстояние, которое прошел первый поезд)
- Теперь мы можем ответить на главный вопрос? (Нет, так как мы не знаем, сколько часов ехал второй поезд)
- Можем это узнать? (Да)
- Как узнаем? (Надо расстояние, которое прошел второй поезд, разделить на время)
- А сейчас можем ответить на главный вопрос? (Да)
- Что для этого нужно сделать? (Надо из времени, которое шел первый поезд, вычесть то время, которое шел второй поезд)
- Итак, во сколько действий решили задачу? (В 4 действия)
- Записываем решение:
1) 416: 52 = 8 (ч) – шел первый поезд.
2) 782 – 416 = 366 (км) – прошел второй поезд.
3) 366: 61 = 6 (ч) – шел второй поезд.
4) 8 – 6 = 2 (ч) – на это время первый поезд вышел раньше второго.
Ответ: на 2 часа.
Задача 5: (№ 1193)
«Собственная скорость катера (скорость в стоячей воде) равна 21,6 км/ч, а скорость течения реки 4,7 км/ч. Найдите скорость катера по течению и против течения реки.»
- Внимательно читаем задачу.
- Давайте построим таблицу к данной задаче.
- О каких величинах идет речь в задаче?
- Запишем данные в таблицу.
| Собств. v (км/ч) | V течения (км/ч) | V по течению реки (км/ч) | V против течения (км/ч) |
| 21,6 | 4,7 | ? | ? |
- То, что неизвестно, обозначим знаком вопроса.
- Что узнаем сначала? (Скорость катера по течению реки)
- Как найдем? (Надо к собственной скорости катера прибавить скорость течения)
- Что можем узнать сейчас? (Скорость катера против течения)
- Что для этого нужно сделать? (Из собственной скорости катера вычесть скорость течения)
- Записываем решение:
1) 21,6 + 4,7 = 26,3 (км/ч) – скорость катера по течению.
2) 21,6 – 4,7 = 16,9 (км/ч) – скорость катера против течения.
Ответ: 26,3 км/ч; 16,9 км/ч.
Задача 6: (№ 1194)
«Скорость теплохода по течению реки равна 37,6 км/ч. Найдите собственную скорость теплохода и его скорость против течения, если скорость течения реки 3,9 км/ч.»
- Внимательно читаем задачу.
- О каких величинах идет речь в задаче?
- Построим таблицу к данной задаче.
- Что уже известно в задаче? (Скорость по течению реки 37,6 км/ч, скорость течения реки 3,9 км/ч)
- Отметим это в таблице.
| Собств. v | V течения | V по течению реки | V против течения |
| ? | 3,9 км/ч | 37,6 км/ч | ? |
- Что нужно найти в задаче? (Собственную скорость и скорость против течения)
- Обозначим неизвестное знаком вопроса.
- Известна скорость теплохода по течению реки и скорость течения. Что можем узнать по этим данным? (Собственную скорость теплохода)
- Что для этого нужно сделать? (Нужно из скорости теплохода по течению вычесть скорость течения реки)
- Зная собственную скорость теплохода и скорость течения реки, что можем узнать? (Скорость теплохода против течения реки)
- Как узнаем? (Нужно из собственной скорости теплохода вычесть скорость течения реки)
- Записываем решение:
1) 37,6 – 3,9 = 33,7 (км/ч) – собственная скорость теплохода.
2) 33,7 – 3,9 = 29,8 (км/ч) – скорость против течения.
Ответ: 33, 7 км/ч; 29,8 км/ч.
Задача 7: (№ 1196)
«Расстояние между городами 156 км. Из них одновременно навстречу друг другу выехали два велосипедиста. Один проезжает в час 13,6 км, а другой 10,4 км. Через сколько часов они встретятся?»
- Внимательно читаем задачу.
- Давайте к этой задаче сделаем чертеж.
- Что нам известно в задаче? (Из двух городов одновременно навстречу друг другу выехали два велосипедиста)
- Отметим это на чертеже.
![]()
![]()
![]()
![]()
![]() 13,6 км/ч 10,4 км/ч
13,6 км/ч 10,4 км/ч
![]()
![]()
tвстр -?.
156 км
- Что еще известно? (Расстояние между городами 156 км; скорость первого велосипедиста – 13,6 км/ч, а скорость второго – 10,4 км/ч)
- Отметим эти данные на чертеже.
- Что нужно найти в задаче? (Через сколько часов встретятся велосипедисты?)
- Можем сразу ответить на данный вопрос? (Нет)
- Почему? (Сначала надо найти скорость сближения)
- Можем ее найти? (Да)
- Как? (К скорости первого велосипедиста прибавить скорость второго)
- А сейчас можем ответить на главный вопрос задачи? (Да)
- Что для этого нужно сделать? (Расстояние между городами разделить на скорость сближения)
- Записываем решение по действиям с вопросами:
1) Какова скорость сближения велосипедистов?
13,6 + 10,4 = 24 (км/ч)
2) Через сколько часов встретятся велосипедисты?
156 : 24 = 6,5 (ч)
Ответ: через 6,5 часа.
Задача 8: (№ 1233)
«Автомашина в первый час прошла 48,3 км, во второй час она прошла на 15,8 км меньше, чем в первый, а в третий час – на 24,3 км меньше, чем за первые два часа вместе. Какой путь прошла автомашина за эти три часа?»
- Читаем внимательно задачу.
- Для решения данной задачи сделаем схему.
- Что известно в задаче? (Машина в первый час прошла 48,3 км, во второй – на 15,8 км меньше, чем в первый, а в третий час – на 24,3 км меньше, чем за первые два часа вместе)
![]() - Отметим это на схеме.
- Отметим это на схеме.
![]() 1 ч.
1 ч.
48,3 км
![]()
![]()
![]()
![]()
![]() 2 ч. ?
2 ч. ?
? 15,8 км
![]()
![]()
![]() 3 ч.
3 ч.
? 24,3 км
- Какой главный вопрос задачи? (Какой путь прошла автомашина за эти три часа?)
- Можем сразу на него ответить? (Нет)
- Почему? (Мы не знаем расстояние, которое проехала автомашина во второй час)
- Можем это узнать? (Да)
- Как? (Надо из пути, пройденного в первый час, вычесть 15,8 км)
- А сейчас можем ответить на вопрос задачи? (Нет)
- Почему? (Сначала надо узнать, какой путь прошла автомашина за третий час)
- Можем это узнать? (Нет)
- Почему? (Не знаем путь, который прошла машина за 1 и 2 час)
- Можем его найти? (Да)
- Как найдем? (Надо сложить путь, пройденный за 1 и 2 час)
- Сейчас можем найти путь, который прошла машина за третий час? (Да)
- Как узнаем? (Надо из расстояния, которое прошла машина за 1 и 2 час вычесть 24,3 км)
- Теперь можем найти путь, который прошла машина за три часа? (Да)
- Как найдем? (Расстояния, пройденные за каждый час, нужно сложить)
- Записываем решение:
1) 48,3 – 15,8 = 32,5 (км) – прошла машина за 2-ой час.
2) 48,3 + 32,5 = 80,8 (км) – прошла машина за 1 и 2 час.
3) 80,8 – 24,3 = 56,5 (км) – прошла машина за 3-ий час.
4) 56,5 + 80,8 = 137,3 (км) – прошла машина за 3 часа.
Ответ: 137,3 км.
Вывод:
Конструируя работу над задачей, автор попытался показать разный путь анализа задачи (восходящий и нисходящий), использование разных вспомогательных и решающих моделей. [Приложение 2]
Учитель вправе выбрать то, что считает нужным, исходя из подготовленности детей класса, в котором он работает.
При решении задач на движение широко используется метод моделирования, что способствует сознательному и прочному усвоению материала.
Модели помогают ученикам в сознательном выявлении скрытых зависимостей между величинами, побуждают активно мыслить, искать наиболее рациональные пути решения задач. Моделирование наглядно представляет соотношения между данными и искомыми величинами.
При решении задач на движение используются разные виды моделей, например, схематический чертеж, таблица. Использование таблицы предполагает уже хорошее знание учениками взаимозависимостей, так как сама таблица этих зависимостей не показывает.
Опираясь на чертеж, учащиеся находят возможный путь решения задачи. Решающей моделью может быть: выражение, система уравнений, запись решения задачи по действиям. Поскольку на этих моделях происходит решение задачи. Используя визуальную информацию, учатся анализировать задачу и составлять полный план ее решения. Чертеж дает возможность учащимся найти не один, а несколько способов решения.
Основными методами решения задач являются арифметический и алгебраический, а процесс решения задачи включает следующие основные этапы:
1) анализ;
2) поиск плана решения;
3) осуществление плана решения;
4) проверка пройденного решения.
Рассмотрены некоторые приемы выполнения этих этапов. Главный прием – это моделирование. Прежде всего, решить текстовую задачу – это значит построить ее математическую модель. Но чтобы облегчить поиск математической модели, нужны модели вспомогательные. Они могут быть графическими (рисунок, условный рисунок, чертеж, схематический чертеж), знаковыми (краткая запись, таблица).
Метод моделирования позволяет активизировать познавательную деятельность учащихся на уроке.
Похожие работы
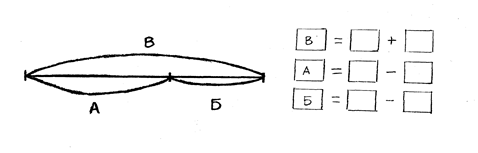
... , заполняя клетки таблицы, школьники должы обратить внимание на совпадение парных сумм, например: 35+47=45+37=82. А + В А В 43 45 47 49 33 35 37 39 2.2. Обучение решению задач на движение с помощью схематического моделирования На подготовительном этапе на ...
... искомой величины в зависимости от изменения данных величин; помогает сделать обобщения теоретических знаний; развивает самостоятельность и вариативность мышления. Использование моделирования при работе над задачами на движение в 5 классе Использование моделей при решении задач на движение по теме «Десятичные дроби» (учебник «Математика» автор Н. Я. Виленкин) Задача 1: (№ 1142) «Из ...
... по развитию творческого мышления учащихся, позволяет развивать у них целостное и системное понимание математических закономерностей и взаимосвязей. Глава II. Анализ практического применения методики обучения решению текстовых задач алгебраическим способом Итак, задачи (в широком смысле этого слова) играют огромную роль в жизни человека. Задачи, которые ставит перед собой человек, и задачи ...
... и перенести полученные знания на практику. Глава 2. Работа учителя по развитию логического мышления на уроках математики 2.1 Опытно-экспериментальная работа и анализ ее результатов Опытно-экспериментальное исследование по выявлению уровня развития логического мышления школьников при решении текстовых задач проводилось на базе МОУ «Средняя общеобразовательная школа № 10» г. Кунгура в ...





0 комментариев