Навигация
2.3 Стратегия С
Стратегия С - восстановление системы проводится только в заранее назначенные моменты времени независимо от отказов системы.
Для исследуемой в настоящем параграфе системы предполагается, что время самостоятельного проявления отказа разно бесконечности, т. е. появившийся в системе отказ самостоятельно не проявляется. Для такой системы планируется проведение различных восстановительных работ (плановых), при которых отказы обнаруживаются, устраняются и предупреждаются.
Пусть при t=0, когда начинается эксплуатация системы, назначается проведение плановых восстановительных работ через случайное время з, распределенное по закону G(x). Если к назначенному моменту з система не отказала (о>з, где о — время безотказной работы, распределенное по закону F(x)), то в этот момент проводится плановая предупредительная профилактика, которая полностью обновляет систему и средняя длительность которой равна Тpp. Если к назначенному моменту система отказала (о≤з), то в этот момент проводится плановый аварийно-профилактический ремонт, который полностью обновляет систему и длится в среднем время Тap. После окончания плановых работ весь процесс обслуживания полностью повторяется.
Определим случайный процесс x(t), характеризующий состояние системы в момент t, x(t) :
· E0, если в момент t система работоспособна и проработает еще время, большее z≥0;
· E1, если в момент t система работоспособна, но до отказа проработает время, меньшее z,
· E2, если в момент t система простаивает в неработоспособном состоянии (скрытый отказ);
· E3, если в момент t в системе проводится плановый аварийно-профилактический ремонт;
· E4, если в момент t в системе проводится плановая предупредительная профилактика.
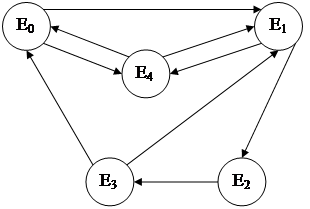
Рисунок 3 – Диаграмма переходов процесса x(t) (Стратегия С)
Описанный процесс является регенерирующим (например, моментами регенерации являются моменты попадания в состояние То), а в предположении, что время, ремонта - непрерывная случайная величина, и апериодическим. При длительной эксплуатации системы характеристики качества функционирования выражаются дробно-линейным функционалом.
Как и ранее, будем предполагать, что функция распределения времени безотказной работы F(х) известна лишь в отдельных точках. F(x) Є Щ(n,y,р). Задача состоит в том, чтобы определить гарантированную среднюю величину функционала I(G,F) , т. е.
I(G*,F*) = max min I(G,F), где G Є Щ, F Є Щ(n,y,р).
и функцию G*(x), на которой это значение достигается. Если функционал (2.2.1) характеризует потери, то по G Є Щ берется минимум, a по F Є Щ(n,y,р) - максимум.
Расчёт по статистическим данным :
Методика определения минимаксных периодов проведения плановых предупредительных профилактик и гарантированных значений показателей качества функционирования
Исходные данные для расчета:
· вектор y = (y0=0,y1,y2,…,yn) и вектор р = (р0=0, р1, р2,…, рn);
· средняя длительность плановой предупредительной профилактики Тpp;
· средняя длительность внепланового аварийно-профилактического ремонта Тap;
· потерн за единицу времени при проведении плановой предупредительной профилактики Сpp ;
· потери за единицу времени при проведении внепланового аварийно-профилактического ремонта Сap;
· прибыль C0 , получаемая за единицу времени безотказной работы системы;
· оперативное время Z работы системы, необходимое для выполнения задачи;
· потери за единицу времени при наличии в системе скрытого отказа Сp.
Формулы для расчета минимаксных периодов и гарантированных значений показателей качества функционирования :
· Коэффициент готовности.
Определяется номер k0, при котором достигается максимум из выражений :
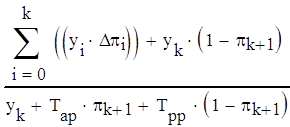 , (3.1)
, (3.1)
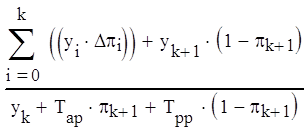 , (3.2)
, (3.2)
при k = 0,1,2,..., n.
Если выражение (2.1) больше (2.2 ), то профилактики целесообразно проводить через время ф = yk0 + 0 и гарантированное значение коэффициента готовности равно (2.1). Если выражение (2.1) меньше (2.2 ), то профилактики целесообразно проводить через время ф = yk0+1 - 0 и гарантированное значение коэффициента готовности равно правой части этого неравенства.
· Вероятность выполнения задачи.
Определяется номер k0(0≤k0≤n), для которого yk0 – z ≤ 0, yk0+1 – z > 0. Далее определяется максиму отношения выражения (2.3) к (2.4).
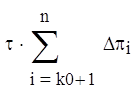
![]()
, при ф [0 , yk0+1 - z],
(3.3)
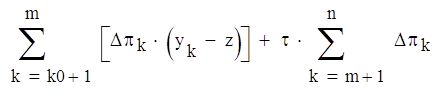
, при ф [ym – z , ym+1 – z].
Ф + Tап рk+1 + Tпп (1 – рk+1) , при ф [yk , yk+1], k = 0,1,2,…, n (3.4)
Точка ф, при которой достигается этот максимум, определяет минимаксный период проведения предупредительных профилактик, а значение этого максимума есть гарантированное значение вероятности выполнения задачи.
· Средние удельные затраты.
Определяется номер k0, при котором достигается минимум из выражений :
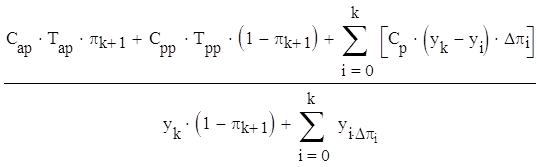 (3.5)
(3.5)
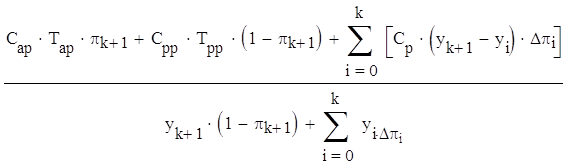 (3.6)
(3.6)
Если при этом выражение (2.5) меньше (2.6), то предупредительную профилактику целесообразно проводить через время ф = yk0 + 0 и гарантированное значения средних удельных потерь равно (2.5). Если выражение (2.5) больше (2.6), то предупредительные профилактики целесообразно проводить через время ф = yk0+1 – 0 и гарантированное значение средних удельных потерь будет равно (2.6).
· Средняя удельная прибыль.
Определяется номер k0, при котором достигается максимум выражения:
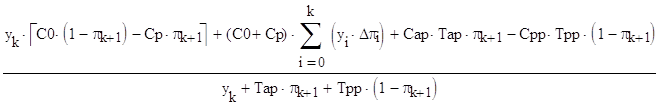 (3.7)
(3.7)
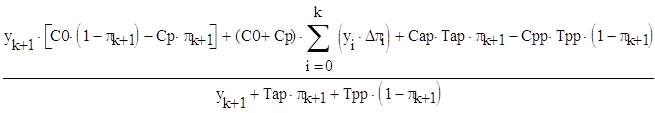 (3.8)
(3.8)
Если при этом максимум совпадает с выражением (2.7), то предупредительные профилактики целесообразно проводить через время ф = yk0 - 0. а гарантированное значение средней удельной прибыли равно первому выражению. Если максимум совпадает с выражением (2.8), то предупредительные профилактики целесообразно проводить через время ф = yk0+1 - 0, а гарантированное значение средней удельной прибыли равно этому второму выражению при k=k0.
Расчёт по функции распределения времени безотказной работы системы :
Исходные данные для расчета:
· функция распределения времени безотказной работы системы F(t);
· средняя длительность плановой предупредительной профилактики Тpp;
· средняя длительность внепланового аварийно-профилактического ремонта Тap;
· потерн за единицу времени при проведении плановой предупредительной профилактики Сpp ;
· потери за единицу времени при проведении внепланового аварийно-профилактического ремонта Сap;
· прибыль C0 , получаемая за единицу времени безотказной работы системы;
· оперативное время Z работы системы, необходимое для выполнения задачи;
· потери за единицу времени при наличии в системе скрытого отказа Сp.
· Коэффициент готовности :
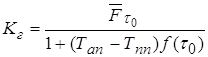 (3.9)
(3.9)
· Средние удельные затраты :
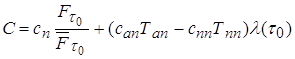 (3.10)
(3.10)
· Средняя удельная прибыль :
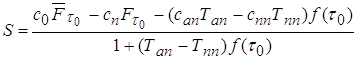 (3.11)
(3.11)
· Вероятность выполнения задачи :
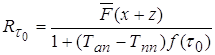 (3.12)
(3.12)
Пример. Определим гарантированные значения показателей качества функционирования и сроки проведения плановых предупредительных профилактик системы, для которой заданы следующие исходные характеристики:
Tpp = 1 ч; Тap = 2 ч; сpp=1 ед/ч; сap=2 ед/ч; z = 25 ч; с0 = 5 ед/ч;
Сp = 2 ед/ч;
y = (y0 = 0;.y1 = l0; у2 = 20; у3 = 30; у4 = 40),
р = (р0 = 0; р1 = 0,1; р2 = 0.15; р3 = 0,3; р4 = 0,5).
· Коэффициент готовности.
Значения (3.1) и (3.2) для различных k сведены в таблицу №3.1:
Таблица №3.1 – Величины коэффициента готовности
| k = 0 | k = 1 | k = 2 | k = 3 | k = 4 |
| 0 0,818 | 0,807 0,822 | 0,821 0,783 | 0,736 0,71 | 0,702 0 |
Итак, получили, что предупредительную профилактику целесообразно проводить через время ф =20 - 0 ч. и гарантированное значение коэффициента готовности равно 0,822.
· Вероятность выполнения задачи.
Определим величину k0. В рассматриваемом случае k0=2.
Далее определяем величины отношений в точках вида уk± 0 ,уk - z. Результаты сведены в таблицу №3.2:
Таблица №3.2 – Величины вероятности выполнения задачи
| y=0 | y=5 - 0 | y=5 + 0 | у=10 - 0 | у =10 + 0 | у=20 - 0 | y=20+0 |
| 0 | 0.70 | 0.57 | 0.54 | 0,53 | 0,52 | 0,40 |
Максимум вероятности 0,7 достигается при ф =5 - 0 ч.
· Средние удельные затраты.
Вычисляем величины средних удельных затрат при различных k. Результаты сведены в таблицу №3.3.
Таблица №3.3 – Величины средних удельных затрат
| k = 0 | k = 1 | k = 2 | k = 3 | k = 4 |
| ∞ 0,378 | 0,383 0.369 | 0,394 0.526 | 0,630 0,783 | 0,833 ∞ |
Таким образом, результаты расчета показывают, что предупредительную плановую профилактику целесообразно проводить через время ф = 20 - 0 ч. и при этом гарантированное значение средних удельных потерь будет равно 0,369 ед/ч.
· Средняя удельная прибыль.
Вычисляем значения средней удельной прибыли для различных k. Результаты сведены в таблицу №3.4:
Таблица №3.5 – Величины средней удельной прибыли
| k = 0 | k = 1 | k = 2 | k = 3 | k = 4 |
| <0 3,72 | 3,70 3,84 | 3,80 8,48 | 3,48 0,30 | 0,29 <0 |
Итак, результаты расчета показывают, что предупредительные профилактики целесообразно проводить через время ф = 20 - 0 ч и при этом гарантированное значение средней удельной прибыли равно 3,84 ед/ч.
Результаты вычислений представлены в таблицах 3.6 и 3.7.
Таблица №3.6 - Расчёт по функции распределения.
| Стратегия | Kг | Pвып | Cпр | Cпот |
| Стратегия C | 0,89 | 0,71 | 3,70 | 0,38 |
Таблица №3.7 - Расчёт по статистическим данным.
| Стратегия | Kг | Pвып | Cпр | Cпот |
| Стратегия C | 0,80 | 0,70 | 3,95 | 0,37 |
Похожие работы
... дискретного программирование для решения задач проектирование систем обработки данных. - Сформулированы задачи диссертационного исследования. 2. БЛОЧНО-СИММЕТРИЧНЫЕ МОДЕЛИ И МЕТОДЫ ПРОЕКТИРОВАНИЯ СИСТЕМ ОБРАБОТКИ ДАННЫХ В данном разделе рассматриваются общая постановка блочно-симметричной задачи дискретного программирования, её особенности и свойства. Разработан общий подход решения задач ...
... вариант программы позволит работать с единой информационной базой с нескольких рабочих мест. Система также содержит средства обеспечения сохранности и непротиворечивости информации. Для того чтобы ориентировочно оценить, во что может обойтись компании автоматизация управления персоналом, следует обратиться к таблице 1.1. Таблица 1.1 - Внедрение, соотношение затрат и стоимостные оценки ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
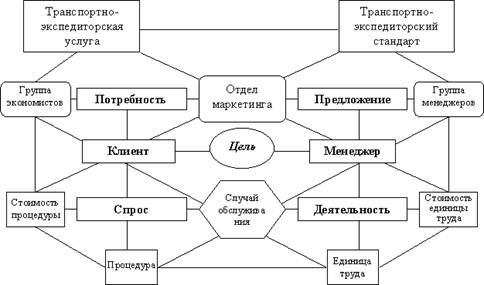
... по специальностям и квалификационным оценкам, возможностям выполнения определенного стандарта, профессиональным и стоимостным характеристикам оценки труда; случай обслуживания (episode фр.) - функция производственной деятельности по предоставлению клиенту комплекса определенных процедур удовлетворяющих его потребности при конкретной цели обращения. Рыночные отношения при предоставлении услуг ...

0 комментариев