Невласні інтеграли з нескінченними межами інтегрування (невласні інтеграли першого роду)

1. Невласні інтеграли з нескінченними межами інтегрування (невласні інтеграли першого роду).

Нехай функція f(х) визначена на проміжку [a;) і інтегрована на будь-якому відрізку [a ; b], де . Тоді, якщо існує скінченна границя

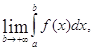 (13),

її називають невласним інтегралом першого роду і позначають так:

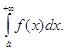 (14)

Таким чином, за означенням

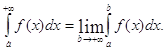 (15)

У цьому випадку інтеграл (14) називають збіжним, а підінтегральну функцію f(x) – інтегрованою на проміжку (а;+).

Якщо ж границя (13) не існує або нескінченна, то інтеграл (14) називають також невласним але розбіжним, а функція f(x) – неінтегровною на [a;).

Аналогічно інтегралу (15) означається невласний інтеграл на проміжку [; b):

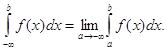 (16)

Невласний інтеграл з двома нескінченними межами визначається рівністю

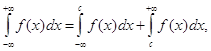 (17)

де с – довільне число. Отже, інтеграл зліва у формулі (17) існує або є збіжним лише тоді, коли є збіжними обидва інтеграли справа. Можна довести, що інтеграл, визначений формулою (17), не залежить від вибору числа с.

З наведених означень видно, що невласний інтеграл не є границею інтегральних сум, а є границею означеного інтеграла із змінною межею інтегрування.

Зауважимо, що коли функція f(x) неперервна і невід’ємна на проміжку [a;) і коли інтеграл (16) збігається, то природно вважати, що він виражає площу необмеженої області (рис. 3.1)

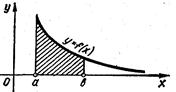
рис. 3.1

Приклад:

Обчислити невласний інтеграл або встановити його розбіжність

а) За формулою (15) маємо

Отже інтеграл а) збігається.

б)

Оскільки ця границя не існує, то інтеграл б) розбіжний.

У розглянутих прикладах обчислення невласного інтеграла ґрунтувалося на його означенні. Проте у деяких випадках немає необхiдностi обчислювати інтеграл, а достатньо знати, збіжний він чи ні.

Теорема 1. Якщо на проміжку функції f(x) і g(x)неперервні і задовольняють умову , то із збіжності інтеграла

 

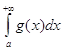 (18)

 

випливає збіжність інтеграла

 

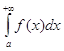, (19)

 

а із розбіжності інтеграла (19) випливає розбіжність інтеграла (18).

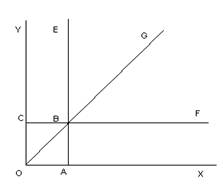
Наведена теорема має простий геометричний зміст (рис. 3.2); якщо площа більшої за розмірами необмеженої області є скiнченне число, то площа меншої області є також скiнченне число; якщо площа меншої області нескінченно велика величина, то площа більшої області є також нескінченно велика величина.

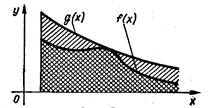
рис. 3.2

Приклад:

Дослідити на збіжність інтеграл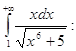

оскільки :

і інтеграл  збігається, то за теоремою 1 заданий інтеграл також збігається.

Теорема 2. Якщо існує границя то інтеграли (18) і (19) або одночасно обидва збігаються, або одночасно розбігаються.

Ця ознака iнодi виявляється зручнішою, ніж теорема 1, бо не потребує перевірки нерiвностi .

Приклад:

Дослідити на збіжність інтеграл

оскільки інтеграл

 збігається і ,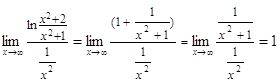

то заданий інтеграл також збігається.

В теоремах 1 і 2 розглядались невласні інтеграли від невід’ємних функцій. У випадку, коли пiдiнтегральна функція є знакозмінною, справедлива така теорема.

Теорема 3. Якщо інтеграл збігається, то збігається й інтеграл .

Приклад:

Дослідити на збіжність інтеграл :

тут підінтегральна функція знакозмінна; оскільки

,

то заданий інтеграл збігається.

Слід зауважити, що із збіжності інтеграла 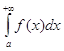 не випливає, взагалі кажучи збіжність інтеграла 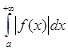. Ця обставина виправдовує такі означення.

Якщо разом з інтегралом 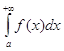 збігається й інтеграл 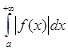, то інтеграл  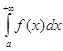називають абсолютно збіжним, а функцію  - абсолютно інтегровною на проміжку .

Якщо інтеграл 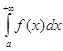 збігається, а інтеграл  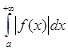розбігається, то інтеграл  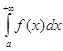називають умовно (або неабсолютно) збіжним.

Тепер теорему 3 можна перефразувати так: абсолютно збіжний інтеграл збігається.

Отже, для знакозмінної функції викладені тут міркування дають змогу встановити лише абсолютну збiжнiсть інтеграла. Якщо ж невласний інтеграл збігається умовно, то застосовують більш глибокі ознаки збiжностi.