Навигация
Невласні інтеграли від необмежених функцій (невласні інтеграли другого роду)
14611
знаков
0
таблиц
7
изображений
2. Невласні інтеграли від необмежених функцій (невласні інтеграли другого роду).
Нехай функція 
визначена на проміжку 
. Точку х=b назвемо особливою точкою функції , якщо 
при 
(рис. 3.3)
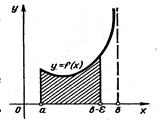
рис. 3.3
Нехай функція на відрізку 
при довільному 
, такому, що 
тоді існує скінченна границя
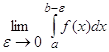, (20)
її називають невласним інтегралом другого роду і позначають так:
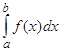(21)
Отже, за означенням
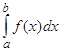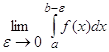= (22)
У цьому випадку кажуть, що інтеграл (21) існує або збігається. Якщо ж границя (20) нескінченна або не існує, то інтеграл (21) також називають невласним інтегралом, але розбіжним.
Аналогічно якщо х=а - особлива точка (рис. 3.4), невласний інтеграл визначається так:
=
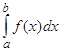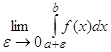
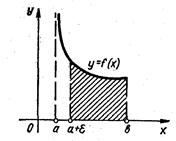
рис. 3.4
Якщо необмежена в околі якої-небудь внутрішньої точки 
, то за умови існування обох невласних інтегралів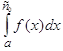 
і 
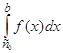за означенням покладають (рис. 3.5)
=+.
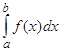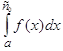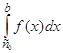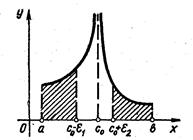
рис. 3.5
Нарешті, якщо а та b — особливі точки, то за умови існування обох невласних iнтегралiв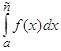 
і 
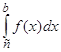за означенням покладають
=+,
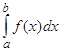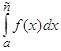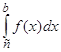де с - довільна точка інтервалу (a;b).
Приклад:
Обчислити невласний інтеграл:
= 
.
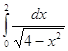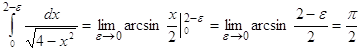Отже інтеграл збіжний.
Сформулюємо тепер ознаки збiжностi для невласних iнтегралiв другого роду.
Теорема 4. Якщо функції і 
неперервні на проміжку [a;b), мають особливу точку х= b і задовольняють умову 
, то із збіжності інтеграла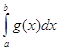 
випливає збіжність інтеграла 
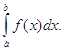, із розбіжності інтеграла 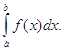випливає розбіжність .
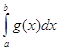Приклад:
Дослідити на збіжність інтеграл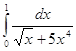 
: заданий інтеграл збігається, бо 
і збігається інтеграл 
.
Теорема 5. Нехай функції 
і 
на проміжку [a;b) неперервні, додатні і мають особливість точці х= b , тоді якщо існує границя
,
то інтеграли 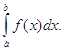і 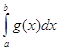або одночасно збігаються, або одночасно розбігаються.
Приклад:
Дослідити на збіжність інтеграл 
: функції f(x)= 
та =
мають особливість у точці х=0. Оскільки 
=
, і інтеграл 
розбігається, то заданий інтеграл також розбігається.
Теорема 6. Якщо х=b – особлива точка функції і інтеграл 
збігається, то інтеграл 
також збігається.
Приклад: дослідити на збіжність інтеграл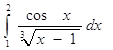 
.
Заданий інтеграл збігається, тому що 
і збігається інтеграл 
.
4.Ефективність реклами. Логістична крива.
Розвиток багатьох процесів у економіці, в тому числі і на підприємствах, відображає логістична крива, яка характеризується часовою чи іншою залежністю параметрів об’єкта. Дану криву ще називають зигзагоподібною (S-подібною), оскільки вона нагадує букву S.
Похожие работы
... поняття визначеного інтеграла на ці випадки, приходимо до невласного інтеграла — інтеграла від функції на необмеженому проміжку або від необмеженої функції. Тому в цій курсовій роботі розглянемо невласні подвійні інтеграли. Метою роботи є вивчення умов існування, властивостей, методів обчислення невласних подвійних інтегралів. Відповідно до мети поставлені наступні завдання: 1. Ввести поняття ...
... і означення Означення: Дифуром називається рівняння, яку містить шукану похідну ф-ії. Найбільший порядок похідних називається порядком диф.рівняння. Означення матрець, типи матрець. Означення: Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпчиків. Їх позначають великими літерами A,B,C і т.д. Типи матрець: Квадратна матриця, в якої елементи головної діагоналі дорівнюють ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... ів Стілтьєса Доведемо наступну теорему: 1. Якщо функція f(x) інтегрована в сенсі Рімана на проміжку [a, b], a g(x) представлена інтегралом де функція абсолютно інтегровна в [а,b], то (11) Існування інтеграла Стілтьєса при зроблених припущеннях уже було доведено вище. Залишається лише з’ясувати рівність (11). Без зменшення загальності можна припустити, ...
0 комментариев